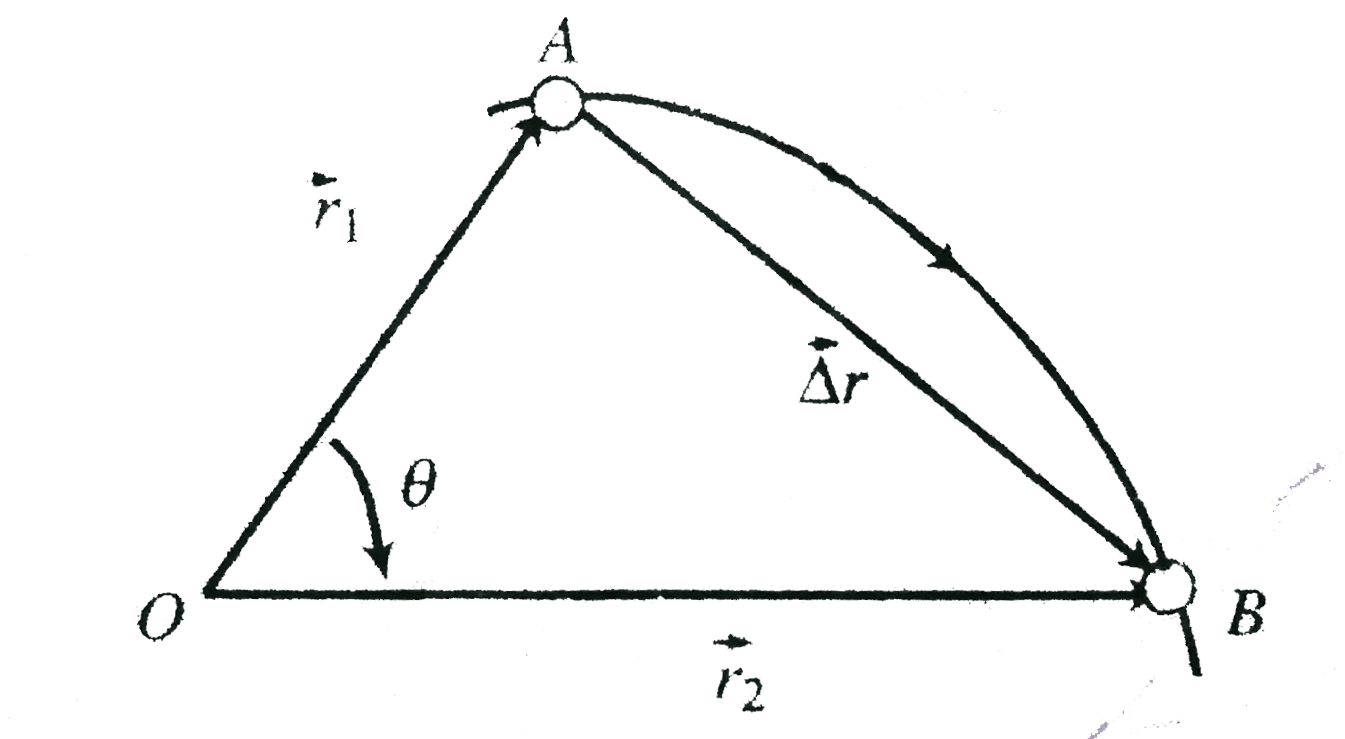
A particle moves from position $A$ to position $B$ in a path as shown in If the poit vectors ${\vec{r}}_{1}$ and ${\vec{r}}_{2}$ making an angle $θ$ between them are give, find the magnitude of displacement.
.

Video Solution

Text Solution

Verified by Experts

From triangle OAB: $\vec{r} + Δ \vec{r} = {\vec{r}}_{2} \Rightarrow {\vec{r}}_{2} - {\vec{r}}_{1} = Δ \vec{r}$
Hence, $| \vec{S} | = | Δ \vec{r} | = | {\vec{r}}_{2} - {\vec{r}}_{1} | = \sqrt{r_{1}^{2} + r_{2}^{2} - 2 r_{2} r_{2} \cos θ}$

|

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
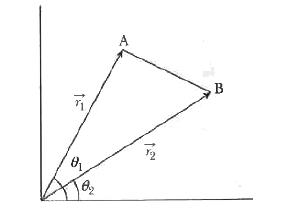
In a two-dimensional motion of a particle, the particle moves from point A of position vector ${\to r}_{1},$ to point B of vectors are , respectively, $r_{1} = 3 and r_{2} = 4$ and the angles they make with the x axis are $θ_{1} = 75^{\circ} and θ_{2} = 15^{\circ},$ respectively, then find the magnitude of the displacement vector.

A15
B $\sqrt{13}$
C $17$
D $\sqrt{15}$
Question 2 - Select One
If $\to e_{1}$ and $\to e_{2}$ are two unit vectors and $θ$ is the angle between them, then $sin (\frac{θ}{2})$ is:
A $\frac{1}{2} | {\to e}_{1} + {\to e}_{2} |$
B $\frac{1}{2} | {\to e}_{1} - {\to e}_{2} |$
C $\frac{{\to e}_{1} . {\to e}_{2}}{2}$
D $\frac{| {\to e}_{1} \times {\to e}_{2} |}{2 | {\to e}_{1} | | {\to e}_{2} |}$
Question 3 - Select One
In a two diamensional motion of a particle, the particle moves from point A, with position vector ${\to r}_{1}$ to point B, with position vector ${\to r}_{2}$ . If the magnitudes of these vectors are, respectively, $r_{1} = 3$ and $r_{2} = 4$ and the angles they make with the x-axis are $θ_{1} = 75^{\circ}$ and $θ_{2} = 15^{\circ}$ , respectively, then find the magnitude of the displacement vector.

A15
B $\sqrt{13}$
C17
D $\sqrt{15}$

CENGAGE PHYSICS-KINEMATICS-1-Integer

Home
Ask Doubt
Profile