A particle moves in a circle with constant angular velocity ω about a point P on its circumference. The angular velocity of the particle about the centre C of the circle is
2ω
ω2
ω
Not constant
The correct Answer is:A
To solve the problem, we need to find the angular velocity of a particle moving in a circle with constant angular velocity ω about a point P on its circumference, with respect to the center C of the circle.
1. Understanding the Motion:
- The particle is moving in a circular path around point P on the circumference of the circle.
- Let's denote the angle covered by the particle as θ when it moves from position A to position B around point P.
2. Relating Angles:
- According to the properties of circular motion, if the angle covered by the point P (the center of rotation for the particle) is θ, then the angle ϕ covered by the particle with respect to the center C of the circle will be 2θ.
- This is because the angle subtended at the center of a circle is always twice the angle subtended at any point on the circumference.
3. Angular Velocity Definition:
- Angular velocity ω is defined as the rate of change of angular displacement with respect to time. Mathematically, it is given by:
ω=dθdt
4. Calculating Angular Velocity about Center C:
- Since the angle ϕ covered by the particle with respect to center C is 2θ, we can express the angular velocity with respect to center C as:
ωC=dϕdt=d(2θ)dt=2dθdt
- Substituting dθdt with ω:
ωC=2ω
5. Conclusion:
- Therefore, the angular velocity of the particle about the center C of the circle is 2ω.
Final Answer:
The angular velocity of the particle about the center C of the circle is 2ω.
---
- The particle is moving in a circular path around point P on the circumference of the circle.
- Let's denote the angle covered by the particle as θ when it moves from position A to position B around point P.
- According to the properties of circular motion, if the angle covered by the point P (the center of rotation for the particle) is θ, then the angle ϕ covered by the particle with respect to the center C of the circle will be 2θ.
- This is because the angle subtended at the center of a circle is always twice the angle subtended at any point on the circumference.
- Angular velocity ω is defined as the rate of change of angular displacement with respect to time. Mathematically, it is given by:
ω=dθdt
- Since the angle ϕ covered by the particle with respect to center C is 2θ, we can express the angular velocity with respect to center C as:
ωC=dϕdt=d(2θ)dt=2dθdt
- Substituting dθdt with ω:
ωC=2ω
- Therefore, the angular velocity of the particle about the center C of the circle is 2ω.
The angular velocity of the particle about the center C of the circle is 2ω.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - A Only One Option is Correct
86 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
A particle moves with constant angular velocity in a circle. During the motion its
View SolutionA particle mass parallel to x-axis with constant velocity v as shown in the figure. The angular velocity of the particle about the origin O
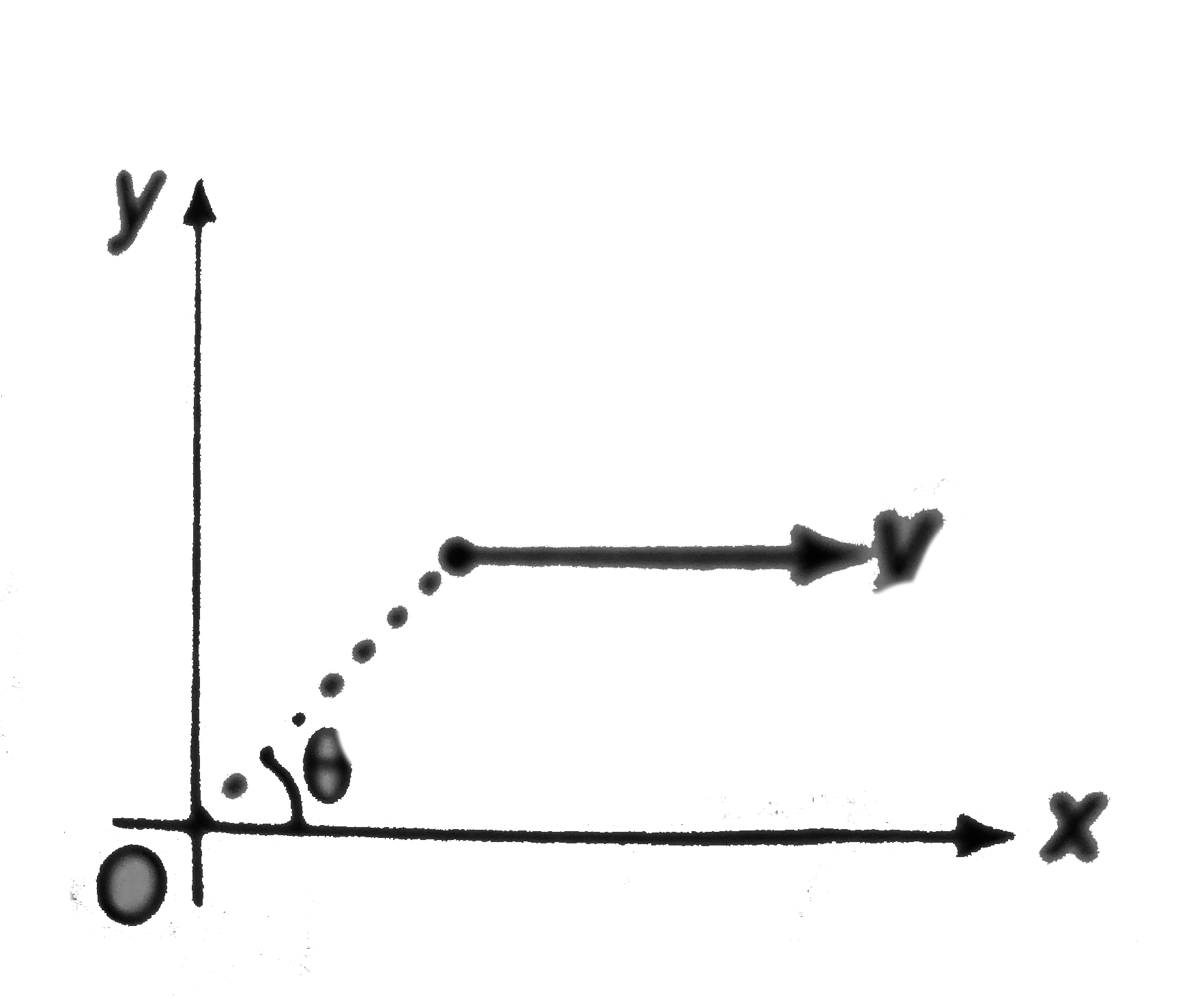
View SolutionA particle is moving with constant speed v along x - axis in positive direction. Find the angular velocity of the particle about the point (0, b), when position of the particle is (a, 0).
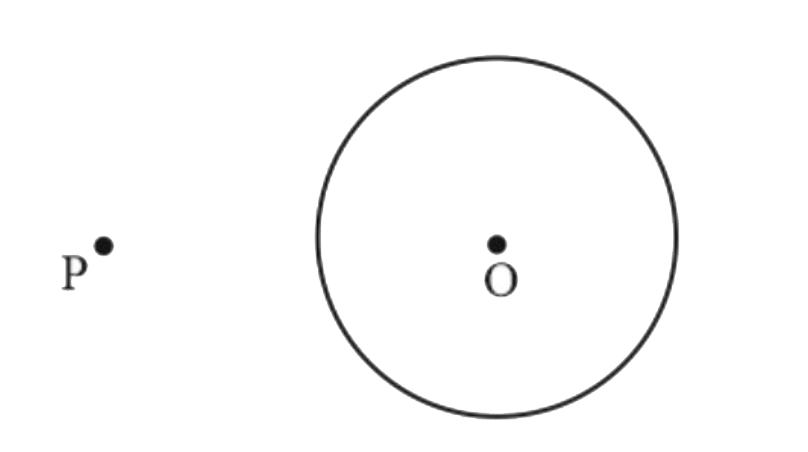
View SolutionConsider a particle , moving in a circle with constant speed . P is a point outside the circle , in the same plane . Then , the angular momentum of the particle about the point P is
View SolutionA particle moves in a circle of radius r with angular velocity ω. At some instant its velocity is v radius vector with respect to centre of the circle is r. At this particular instant centripetal acceleration ac of the particle would be
View SolutionA particle is moving parallel to x-axis as shown in the figure. The angular velocity of the particle about the origin is
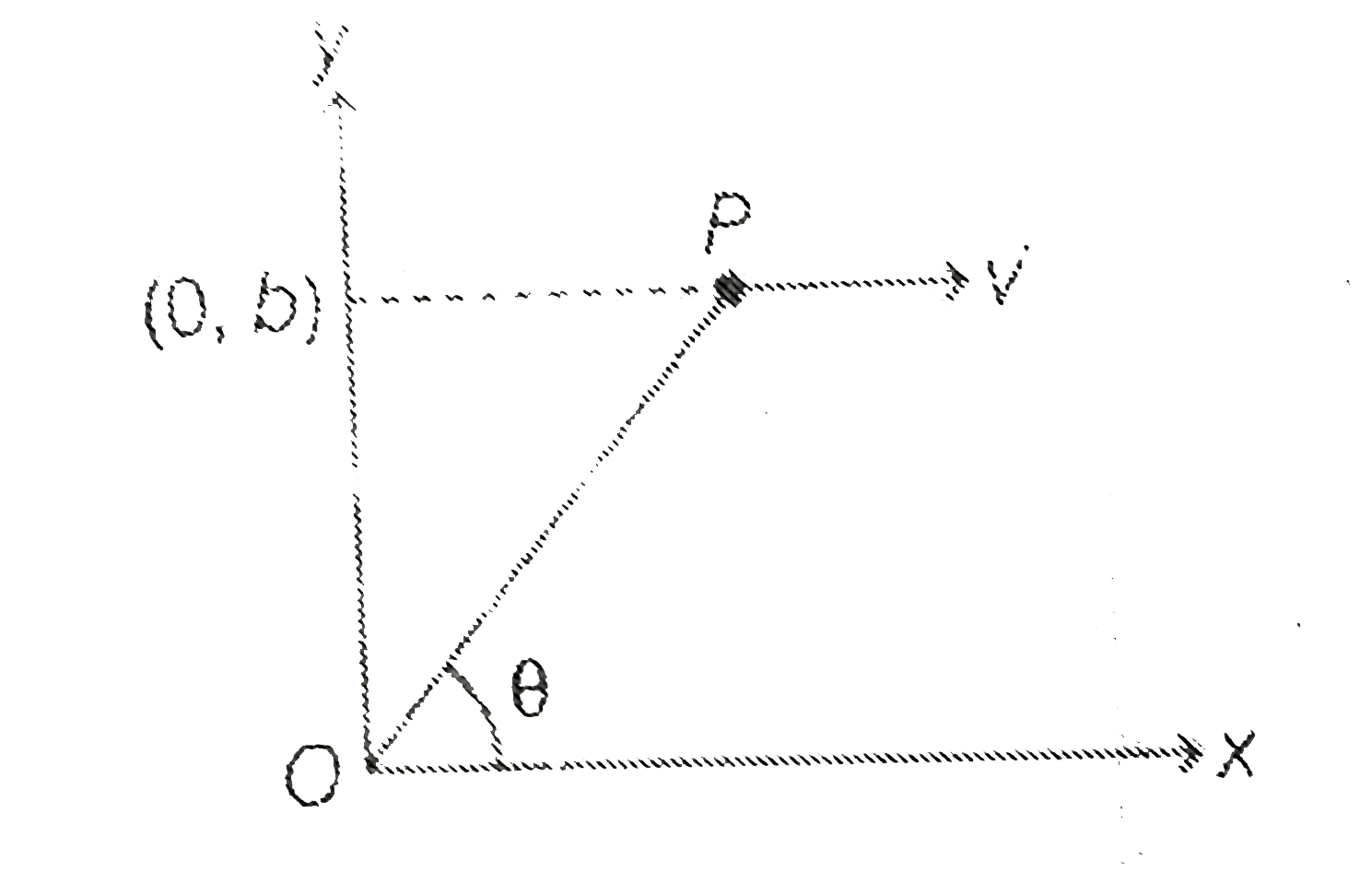
View SolutionIf a point moves along a circle with constant speed, prove that its angular speed about any point on the circle is half of that about the centre.
View SolutionA particle moves in a circular path with constant speed .Find out a point about which the angular momentum of the particle is constant and another point about which changes with time.
View SolutionA rod is rotating with angular velocity ω about axis AB. Find cosθ.

View SolutionA particle moves on a straight line with a uniform velocity. It's angular momentum
View Solution
