A particle moves in the plane xy with constant acceleration 'a' directed along the negative y-axis. The equation of motion of the particle has the form y=px−qx2 where p and q are positive constants. Find the velocity of the particle at the origin of co-ordinates.
The correct Answer is:A
To find the velocity of the particle at the origin of coordinates given the equation of motion y=px−qx2, we can follow these steps:
Step 1: Understand the motion
The equation y=px−qx2 describes the trajectory of the particle in the xy-plane. The acceleration is directed along the negative y-axis, which indicates that the particle is experiencing a downward acceleration.
Step 2: Identify parameters
From the equation of motion, we can identify:
- The coefficient p corresponds to the slope of the trajectory at the origin.
- The coefficient q relates to the curvature of the trajectory.
Step 3: Compare with the general projectile motion equation
The general equation for projectile motion is given by:
y=xtan(θ)−gx22u2(1+tan2(θ))
where:
- g is the acceleration due to gravity (which we can replace with a since the acceleration is constant).
- u is the initial velocity.
- θ is the angle of projection.
Step 4: Match coefficients
By comparing the coefficients from both equations, we can write:
1. p=tan(θ)
2. q=a2u2(1+tan2(θ))
Step 5: Express u in terms of p and q
From the second equation, we can rearrange to find u2:
u2=a2q(1+tan2(θ))
Substituting tan(θ)=p:
u2=a2q(1+p2)
Step 6: Solve for u
Taking the square root to find u:
u=√a2q(1+p2)
Step 7: Conclusion
Thus, the velocity of the particle at the origin of coordinates is given by:
u=√a2q(1+p2)
The equation y=px−qx2 describes the trajectory of the particle in the xy-plane. The acceleration is directed along the negative y-axis, which indicates that the particle is experiencing a downward acceleration.
From the equation of motion, we can identify:
- The coefficient p corresponds to the slope of the trajectory at the origin.
- The coefficient q relates to the curvature of the trajectory.
The general equation for projectile motion is given by:
y=xtan(θ)−gx22u2(1+tan2(θ))
where:
- g is the acceleration due to gravity (which we can replace with a since the acceleration is constant).
- u is the initial velocity.
- θ is the angle of projection.
By comparing the coefficients from both equations, we can write:
1. p=tan(θ)
2. q=a2u2(1+tan2(θ))
From the second equation, we can rearrange to find u2:
u2=a2q(1+tan2(θ))
Substituting tan(θ)=p:
u2=a2q(1+p2)
Taking the square root to find u:
u=√a2q(1+p2)
Thus, the velocity of the particle at the origin of coordinates is given by:
u=√a2q(1+p2)
Topper's Solved these Questions
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Example Type 5
3 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Miscellaneous Examples
4 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Example Type 3
4 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
Similar Questions
A particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
View SolutionA particle moving along the X-axis executes simple harmonic motion, then the force acting on it is given by
where, A and K are positive constants.
View Solution
Knowledge Check
A particle moves in a plane with a constant acceleration in a direction different from the initial velocity. The path of the particle is
Astraight lineBarc of circleCparabolaDellipse
A particle constrained to move along x-axis given a velocity u along the positive x-axis. The acceleration ' a ' of the particle varies as a = - bx, where b is a positive constant and x is the x co-ordinate of the position of the particle . Then select the correct alternative(s): .
View SolutionThe equation of SHM of a particle is d2ydt2+ky=0, where k is a positive constant. The time period of motion is
View SolutionA particle moves in the x-y plane with a constant acceleration of 1.5m/s2 in the direction making an angle of 37∘ with the x-axis.
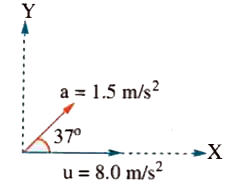
At t=0 the particle is at the origin and its velocity is 8.0m/s along the x- aixs . Find the velocity and the position of the particle at t = 4.0s.
View SolutionA particle movesin the X-Y plane with a constasnt acceleration of 1.5ms2 in the direction making an angle of 370 with the X-axis.At t=0 the particle is at the orign and its velocity is 8.0 m/s along the X-axis. Find the velocity and the position of the particle at t=4.0 s.

View SolutionA particle moves in the XY-plane according to the law x=kt,y=kt(1−αt), where k and α are positive constants and t is time. The trajectory of the particle is
View SolutionA particle of unit mass is moving along x-axis. The velocity of particle varies with position x as v(x). =αx−β (where α and β are positive constants and x>0 ). The acceleration of the particle as a function of x is given as
View SolutionA particle moves in the x−y plane , accoding to the equation, r=(ˆi+2ˆj)Acosωt. The motion of the particle is
View Solution
