A particle moves rectilinearly possessing a parabolic s-t graph. Find the average velocity of the particle over a time interval from t=12s→t=1.5s.
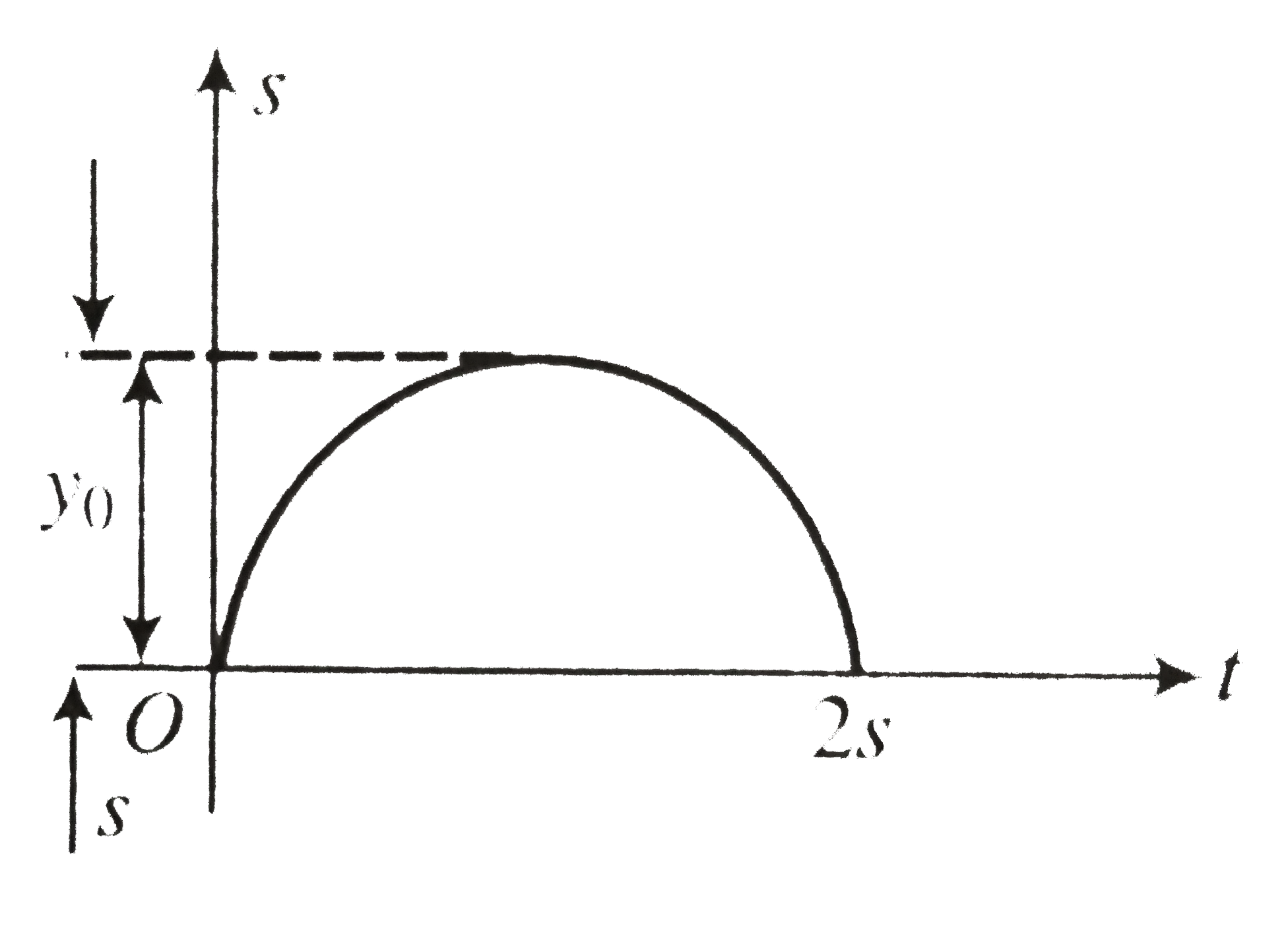
The correct Answer is:0
As s-t graph is a parabola, it can be given as s=k1t−k2t2, where k1andk2 are constants. Since it is symmetrical t = 1 s, we have equal displacements at t=1/2sandt=3/2s that tells us that line AB joining two coordinates is parallel to the t-axis. hence, slope of AB is zero. This implies that the average velocity during the time interval Δt=1 s is zero.
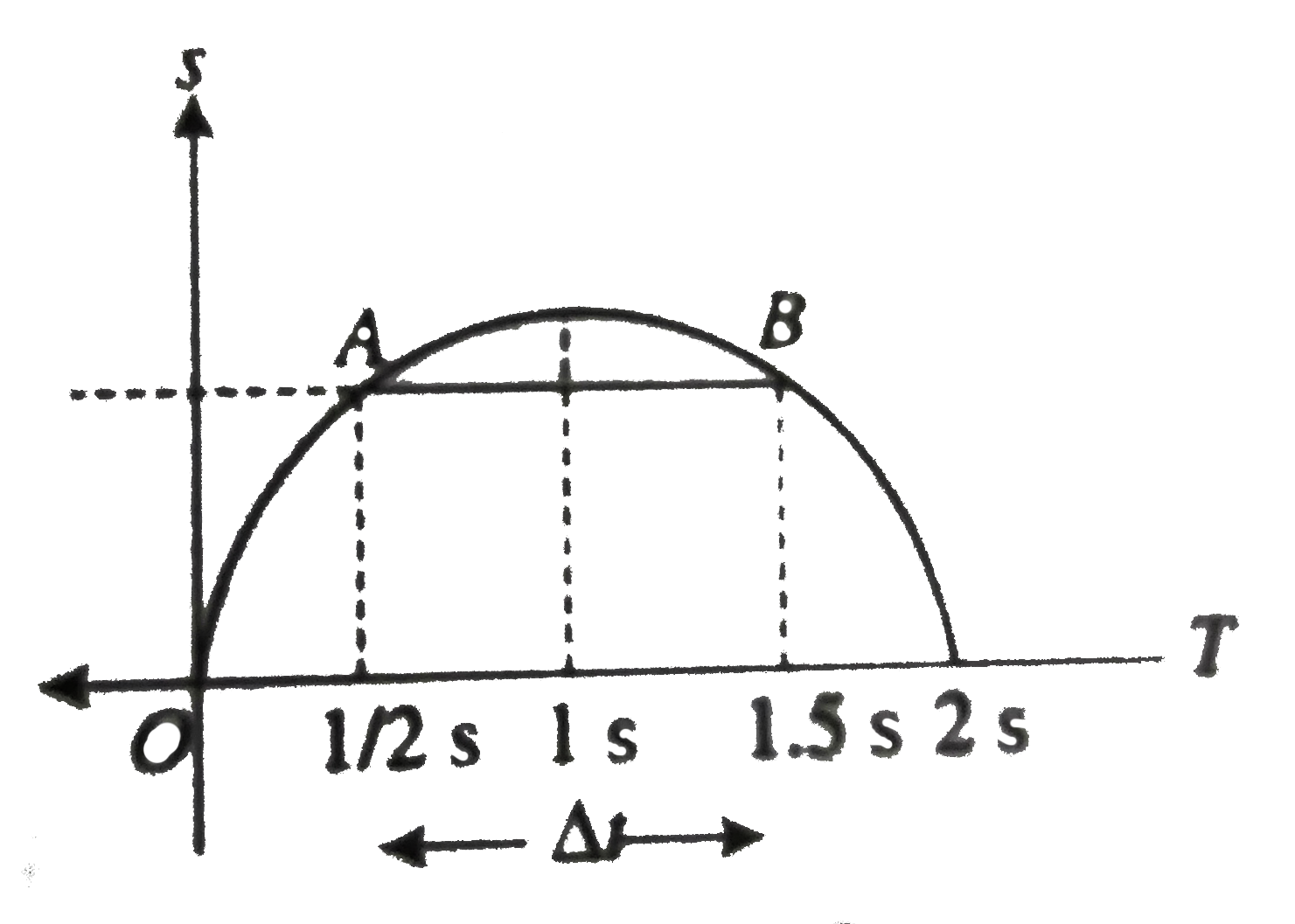
Topper's Solved these Questions
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Fill in the blanks
4 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - True or False
2 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Linked Comprehension Type
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type
9 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
Knowledge Check
The velocity of a particle is zero at time t = 2s, then
Adisplacement must be zero in the interval t = 0 to t = 2 s.Bacceleration may be zero at t = 2 s.Cvelocity must be zero for t>2s .Dacceleration must be zero at t = 2 s.The velocity of a particle varies with time as →v=3ˆi+(4−5t)ˆjms−1. Find the average velocity of the particle for a time interval between t=0 and a time when the speed of the particle becomes minimum.
A(3ˆi+2ˆj)ms−1B(6ˆi+5ˆj)ms−1C(4ˆi+ˆj)ms−1D(3ˆi−5ˆj)ms−1The diagram shows the displacement-time graph for a particle moving in a straight line. Find the average velocity for the interval from t=0 to t=5s.
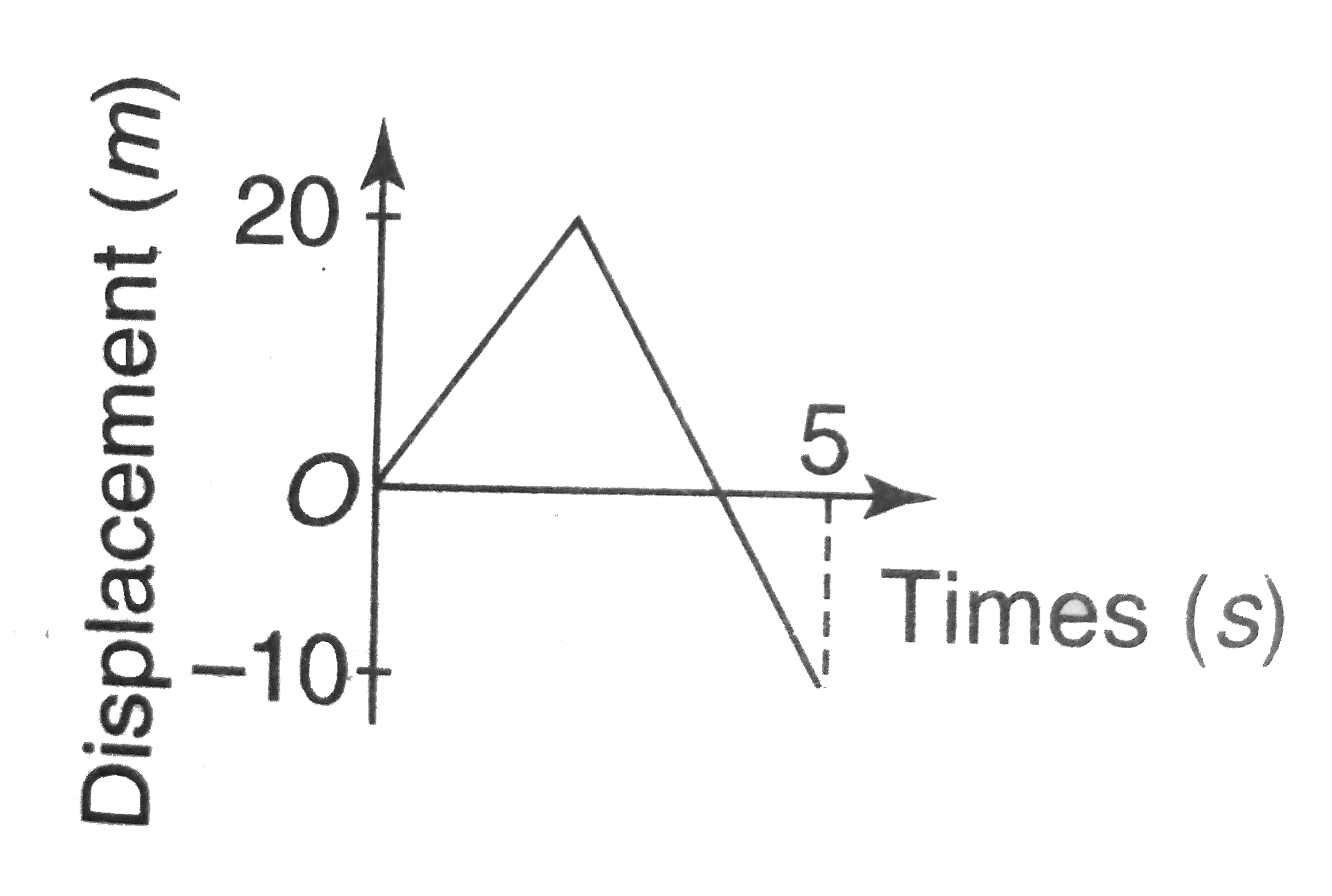 A−2ms−1B2ms−1C−4ms−1D4ms−1
A−2ms−1B2ms−1C−4ms−1D4ms−1
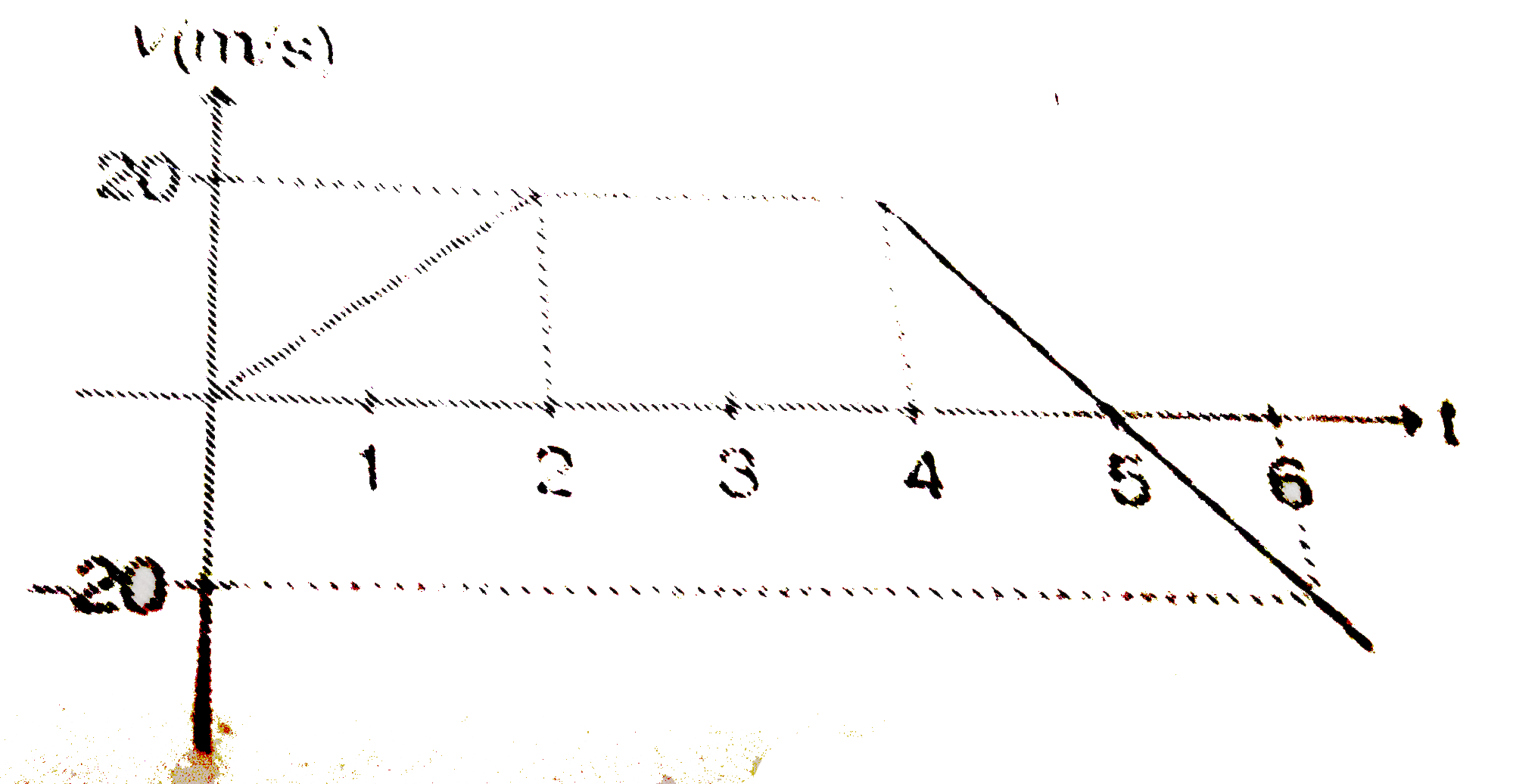
Figure shows the velocity time graph for a particle travelling along a straight line. The magnitude of average velocity (in m/s) of particle during the time interval from t=0 to t=6s is 10α. Find the value of α.
View SolutionThe intantaneous coordinates of a particle are x=(8t−1)m and y=(4t2)m. Calculate (i) the average velocity of the particle during time interval from t=2s to t=4s (ii) the instantaneous velocity of the particle at t=2s.
View SolutionA particle is moving along x-axis such that its velocity varies with time according to v=(3m/s2)t−(2m/s3)t2. Find the velocity at t = 1 s and average velocity of the particle for the interval t = 0 to t = 5 s.
View SolutionThe position (x) - time (t) graph for a particle moving along a straight line is shown in figure. The average speed of particle in time interval t = 0 to t = 8 s is
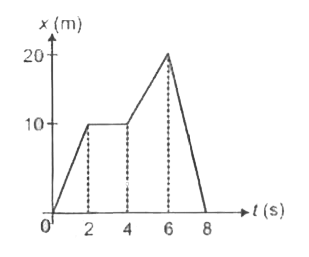
View SolutionThe diagram shows the displacement-time graph for a particle moving in a straight line. Find the average velocity for the interval from t=0 to t=5s.

View Solution
