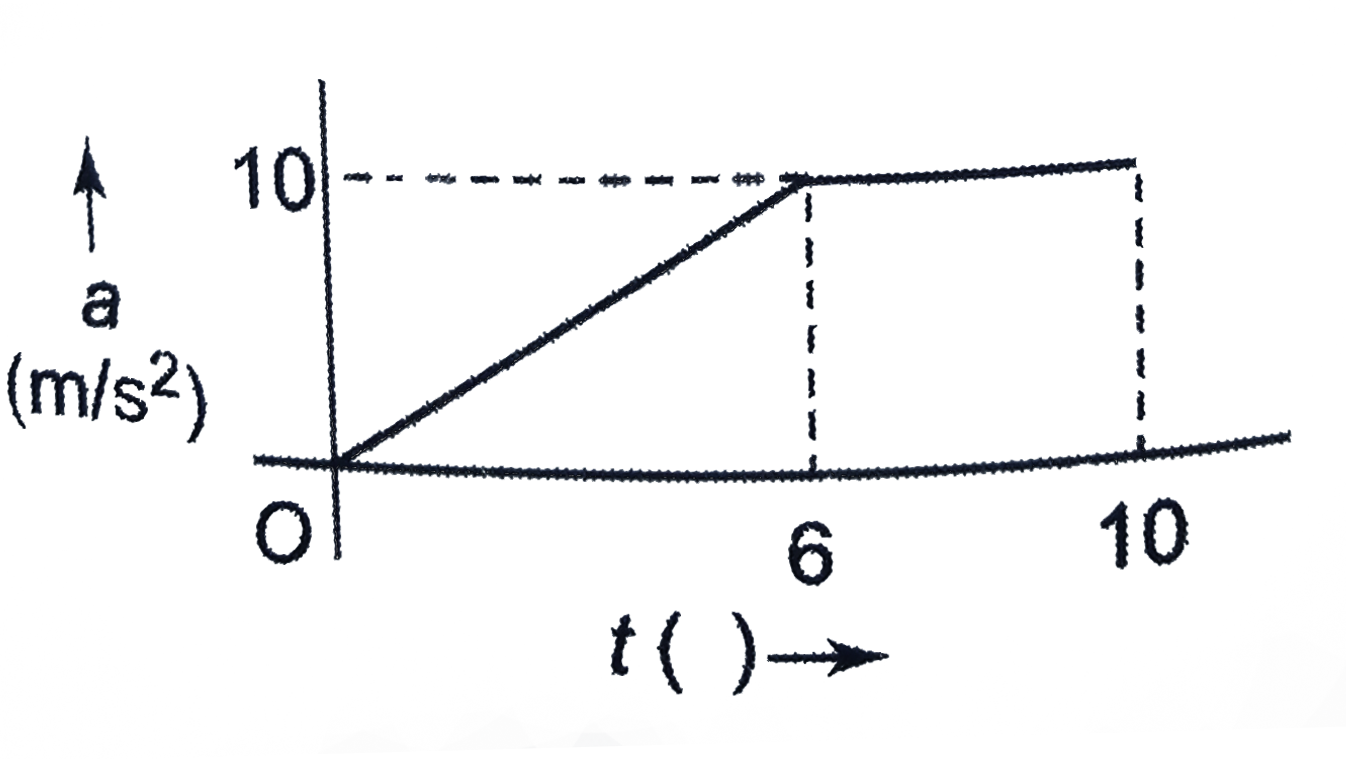
A particle moves vertically with an upward initial speed v0=5m/s. If its acceleration varies with time as shwon in a−t graph in the fig. 4.30, find the velocity of the particle at t=7s.

v=v0+Δv
=v0+A,
where, A=A++A−
=(5×1)+(−12×8×6)
=−19
and v0=+5
Then, v=5−19=−14m/s

Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Problem
14 Videos
- MOTION IN A STRAIGHT LINEBOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Problems and Practice
16 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type
11 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - GRB PUBLICATIONCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - All Questions
210 Videos
Similar Questions
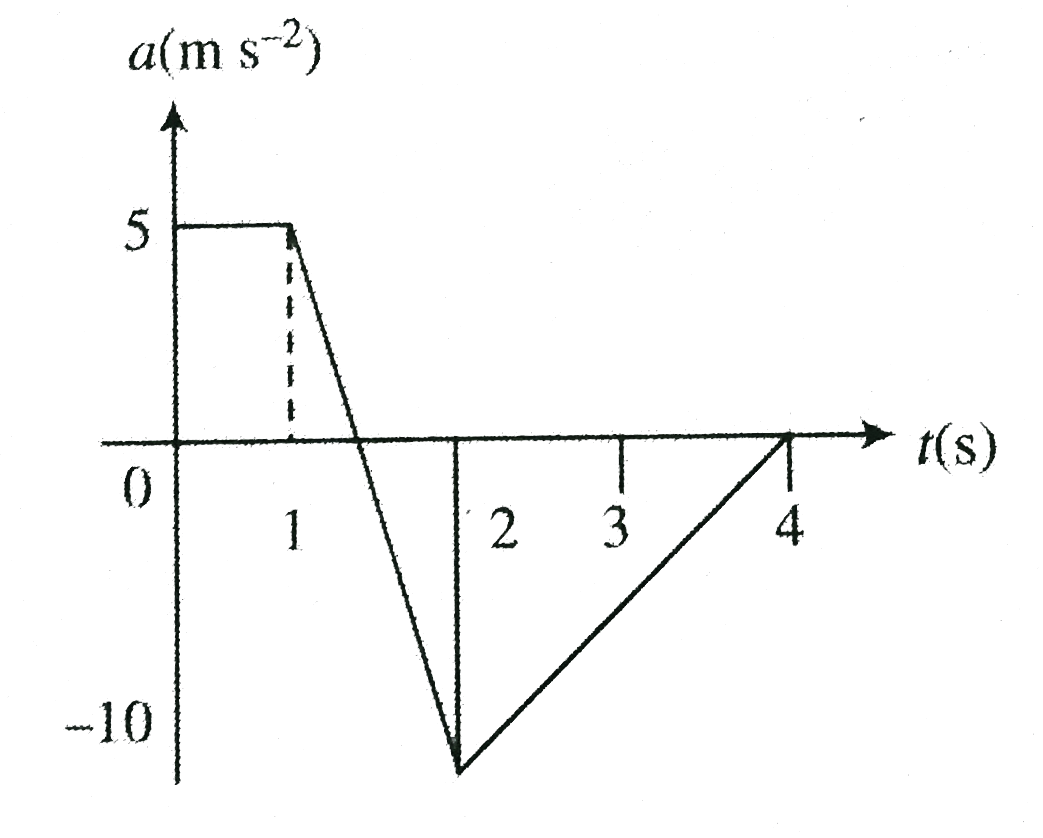
A particle moves vertically with an upwards initial speed v0=10.5ms−1. If its acceleration varies with time as shown in a-t graph in figure, find the velocity of the particles at t = 4s.
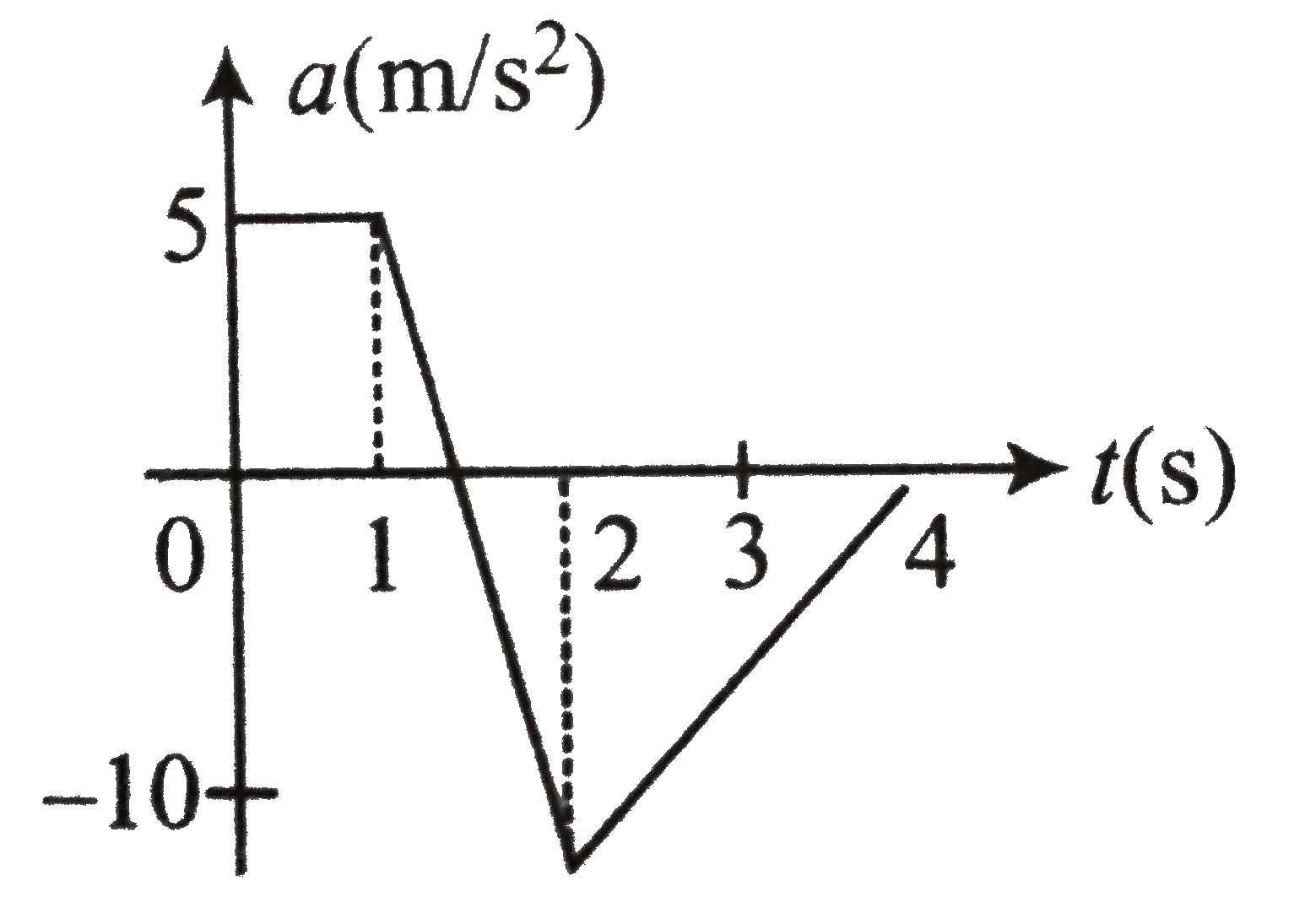
View SolutionA particle moves aling x-axis with an initial speed v0=5ms−1. If its acceleration varies with with time asshown in a−t graph in .
 .
.
a. Find the .
View Solution
Knowledge Check
The acceleration of paticle varies with time as :
a(t)=3t2+4
If the initial velocity of particle is 2m/s, find the velocity of particle at t=3sec.A41m/sB4m/sC39m/sD27m/sFor the acceleration - time (a - t) graph shown in figure, the change in velocity of particle from t = 0 to t = 6 s is
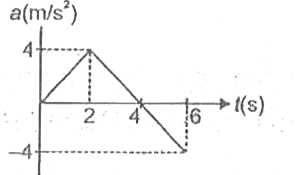 A10 m/sB4 m/sC12 m/sD8 m/s
A10 m/sB4 m/sC12 m/sD8 m/sthe angular velocity omega of a particle varies with time t as ω=5t2+25rads. the angular acceleration of the particle att=1s is
A10rads2B5rads2CZeroD3rads2
A particle initially at rest starts moving along x-axis.Its acceleration varies with time as a=6tm/s^(2) .If it starts from x=10m .Then the position of particle at t=2s is
View SolutionThe displacement x of a particle varies with time as x=4t2–15t+25. Find the position, velocity and acceleration of the particle at t = 0.
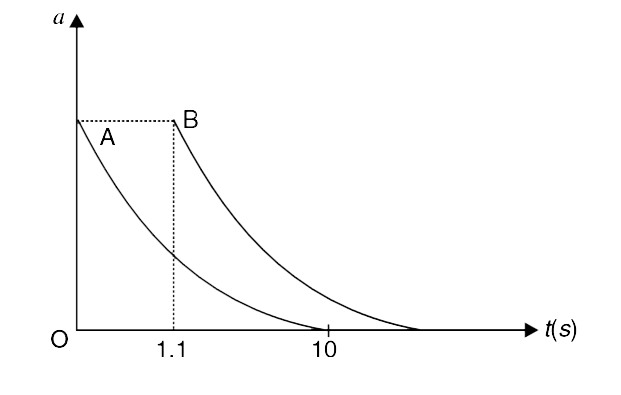
View SolutionParticle A starts from rest and moves along a straight line. Acceleration of the particle varies with time as shown in the graph. In 10 s the velocity of the particle becomes 60m/s and the acceleration drops to zero. Another particle B starts from the same location at time t=1.1s and has acceleration – time relationship identical to A with a delay of 1.1s. Find distance between the particles at time t=15s.
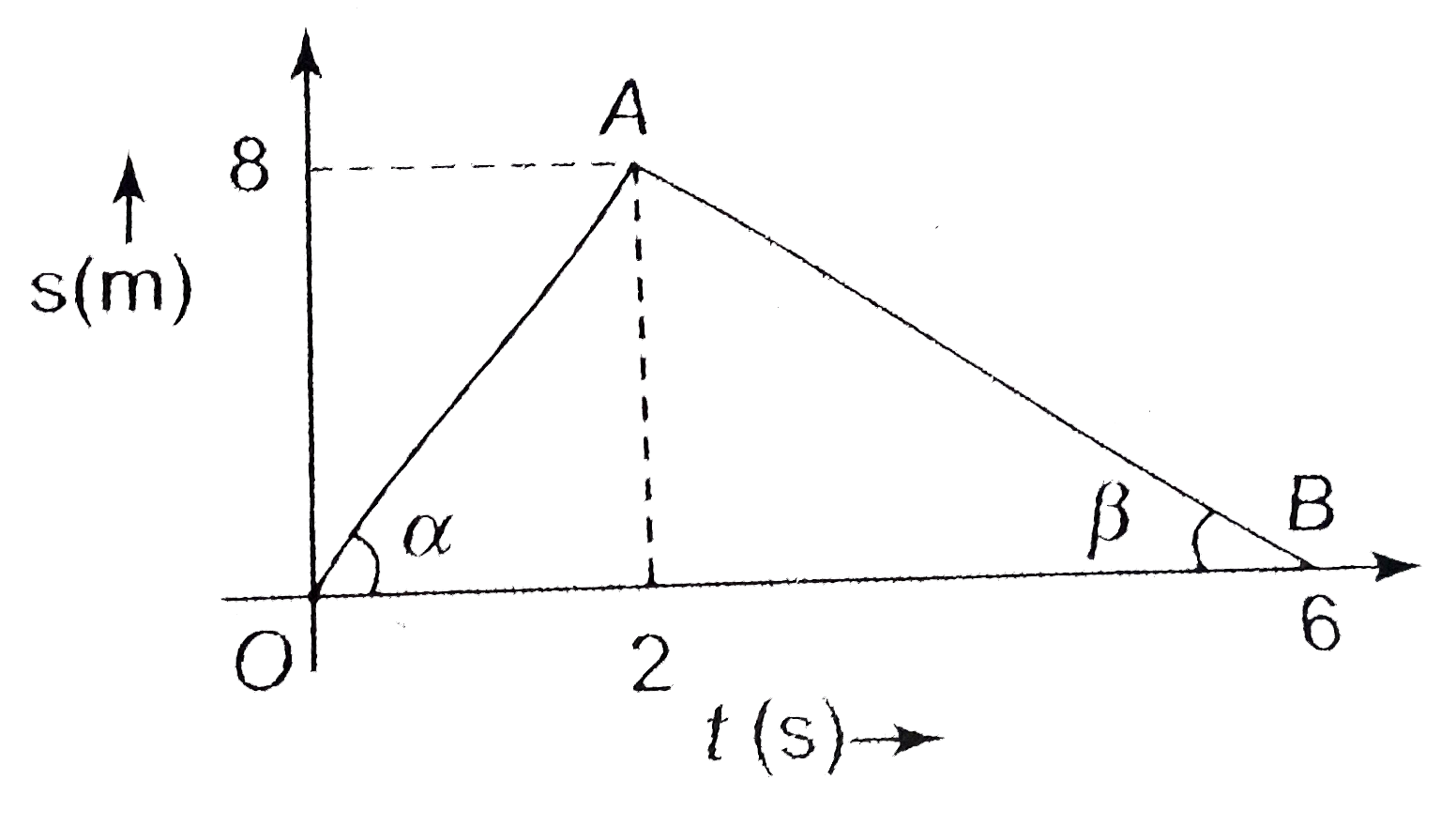
View SolutionFor a particle moving in a straight line, the position-time graph is as shown in the figure. Find the velocity of the particle at time t=1s and t=4s. Also sketch the v-t graph.
View SolutionA particle is moving in a straight line and its acceleration-time graph is shown below. At t=0, the particle is at rest. Find the velocity of the particle at t=3s,6s and 8s. Also sketch the v-s graph.
View Solution
