A particle of charge 3.00μC is separated by 0.120 m from a particle of charge −1.50μC. (a) What is the magnitude of the electrostatic force between them ? (b) What must their separation be to reduce that force by an order of magnitude ?
To solve the problem step by step, we will break it down into two parts as given in the question.
Part (a): Calculate the Magnitude of the Electrostatic Force
1. Identify the Charges and Distance:
- Charge Q1=3.00μC=3.00×10−6C
- Charge Q2=−1.50μC=−1.50×10−6C
- Distance r=0.120m
2. Use Coulomb's Law:
The formula for the electrostatic force F between two charges is given by:
F=k|Q1Q2|r2
where k=9×109N⋅m2/C2 (Coulomb's constant).
3. Substitute the Values:
F=9×109|3.00×10−6×−1.50×10−6|(0.120)2
Since we are interested in the magnitude, we can ignore the negative sign of Q2.
4. Calculate the Force:
F=9×109(3.00×10−6)(1.50×10−6)(0.120)2
=9×1094.50×10−120.0144
=9×109×3.125×10−10
=2.8125N
5. Final Answer for Part (a):
The magnitude of the electrostatic force between the charges is approximately 2.81N.
Part (b): Find the New Separation to Reduce the Force by an Order of Magnitude
1. Determine the New Force:
To reduce the force by an order of magnitude, the new force F′ will be:
F′=F10=2.812510=0.28125N
2. Use Coulomb's Law Again:
We will use the same formula but rearranged to find the new distance r′:
r′=√k|Q1Q2|F′
3. Substitute the Values:
r′=√9×109×(3.00×10−6)(1.50×10−6)0.28125
=√9×109×4.50×10−120.28125
=√40.5×10−30.28125
=√144.0≈12.0m
4. Final Answer for Part (b):
The new separation distance to reduce the force by an order of magnitude is approximately 0.379m.
- Charge Q1=3.00μC=3.00×10−6C
- Charge Q2=−1.50μC=−1.50×10−6C
- Distance r=0.120m
The formula for the electrostatic force F between two charges is given by:
F=k|Q1Q2|r2
where k=9×109N⋅m2/C2 (Coulomb's constant).
F=9×109|3.00×10−6×−1.50×10−6|(0.120)2
Since we are interested in the magnitude, we can ignore the negative sign of Q2.
F=9×109(3.00×10−6)(1.50×10−6)(0.120)2
=9×1094.50×10−120.0144
=9×109×3.125×10−10
=2.8125N
The magnitude of the electrostatic force between the charges is approximately 2.81N.
To reduce the force by an order of magnitude, the new force F′ will be:
F′=F10=2.812510=0.28125N
We will use the same formula but rearranged to find the new distance r′:
r′=√k|Q1Q2|F′
r′=√9×109×(3.00×10−6)(1.50×10−6)0.28125
=√9×109×4.50×10−120.28125
=√40.5×10−30.28125
=√144.0≈12.0m
The new separation distance to reduce the force by an order of magnitude is approximately 0.379m.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Single Correct Choice Type)
45 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (More than one correct Type )
3 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Check points
9 Videos
- ELASTICITYBOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Videos
Similar Questions
Two tiny, spherical water drops, with identical charges of −1.00×10−16C, have a center-to-center separation of 1.20 cm. (a) What is the magnitude of the electrostatic force acting between them ? (b) How many excess electrons are on each drop, giving it its charge imbalance ?
View SolutionTwo point charged bodies q1=3μC, and q2=4μC are separated by 2 m in air. Find the magnitude of electrostatic force between them.
View Solution
Knowledge Check
A −4.0μC charge is located 0.30 m to the left of a + +6.0μC charge. What is the magnitude and direction of the electrostatic force on the positive charge ?
A2.4N to the rightB2.4N to the leftC4.8N to the rightD4.8N to the left
Find the minimum electrostatic force that can exist between two charges separated by distance 1m.
View SolutionAssume that a honeybee is a sphere of diameter 1.000 cm with a charge +60.0pC uniformly spread over its surface . Assume also that a spherical pollen grain of diameter 40.0μC is electrically held on the surface of the bee because the bee's charge induces a charge of 1.00pC on the near side of the grain and a charge of 1+1.00pC on the far side. (a) what is the magnitude of the net electrostatic force on the grain due to the bee ? Next, assume that the bee brings the grain to a distance of 1.000 mm from the tip of a flower's stigma and that the tip is a particle of charge −60.0pC. (b) What is magnitude of the net electrostatic force on the grain due to the stigma ? (c ) Does the grain remain on the bee or move to the stigma ?
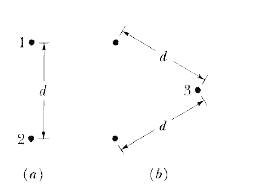
View SolutionIn Fig., particles 1 and 2 have charge 20.0μC each and are held at separation distance d = 0.75 m. (a) What is the magnitude of the electrostatic force on particle 1 due to particle 2? In Fig., particle 3 of charge 20.0μC is positioned so as to complete an equilateral triangle. (b) What is the magnitude of the net electrostatic force on particle 1 due to particles 2 and 3 ?
View SolutionThere are two point charges +4 mu C and -2 mu C .The ratio of magnitude of electrostatic forces acting on them respectively will be
View SolutionTwo equal charges are placed at a separtion of 1.0 m. What should be the magnitude of the charges so that the force between them equals of a 50 kg person?
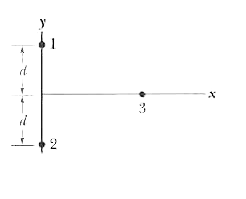
View SolutionIn Fig., particles 1 and 2 of charge q1=q2=+4e are on a y axis at distance d = 1.70 m from the origin. Particle 3 of charge q3=+8e is moved gradually along the x axis from x = 0 to x = +5.0 m. At what values of x will the magnitude of the electrostatic force on the third particle from the other two particles be (a) minimum and (b) maximum ? What are the (c ) minimum and (d) maximum magnitudes ?
View SolutionThe electrostatic force on a small sphere of charge 0.4μC due to anther small sphere of charge −0.8μC in air 0.2 N (i) What is the distance between the two spheres? (ii) What is the force on the second sphere due to the first ?
View Solution
