A particle of charge per unit mass α is released from origin with a velocity →v=v0ˆi in a magnetic field
→B=−B0ˆk for x≤√32v0B0α
and →B=0 for x>√32v0B0α
The x-coordinate of the particle at time t(π3B0α) would be
√32v0B0α+√32v0(t−πB0α)
√32v0B0α+v0(t−π3B0α)
√32v0B0α+v02(t−π3B0α)
√32v0B0α+v0t2
The correct Answer is:C
t=mv0B0q=v0B0α
xr=√32=sinθ∴Θ=60∘
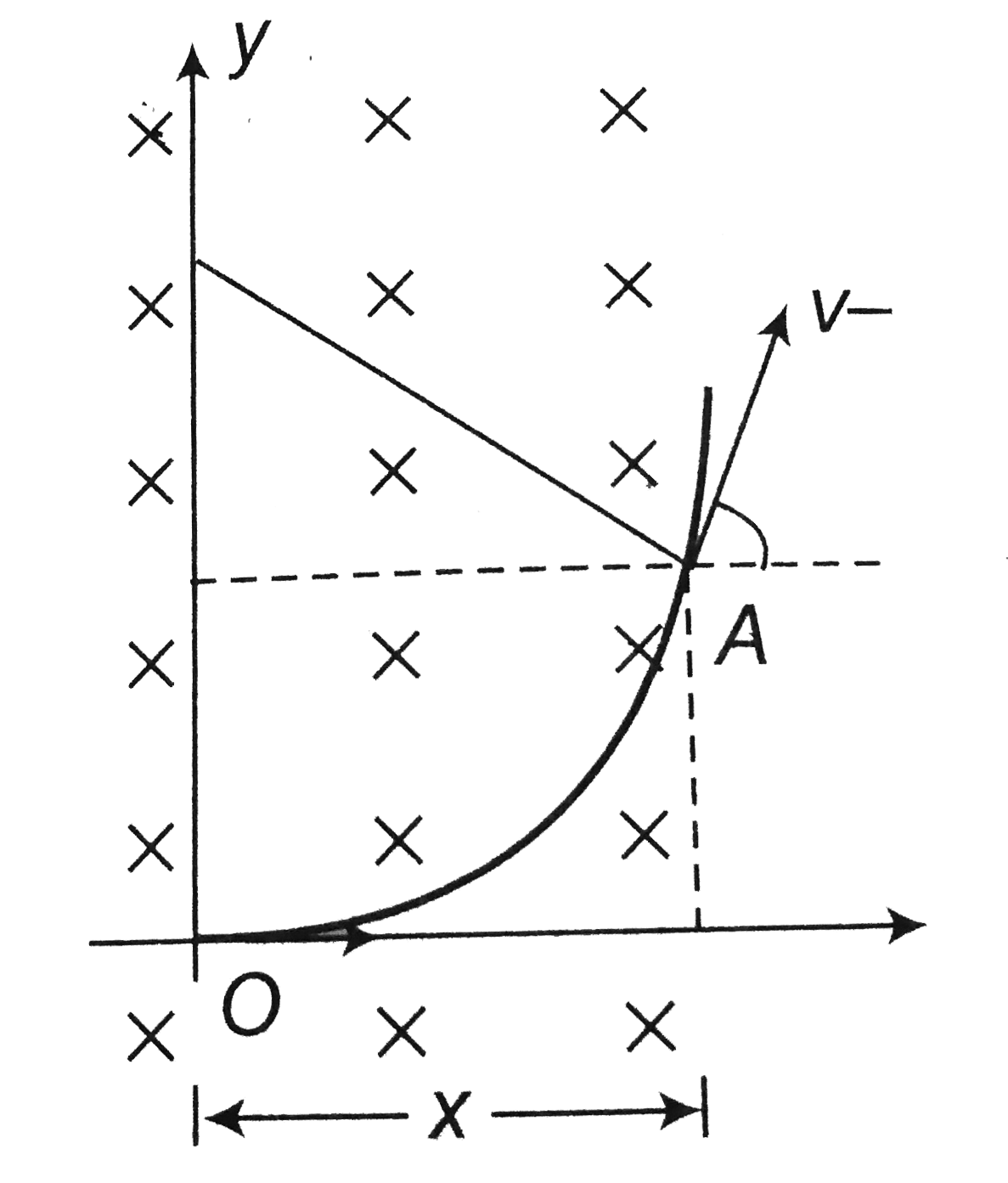
tQA=T6=π3B0α
Therefore x-coordinate of particle at any time
t>π3B0α will be
x=√32v0B0α+v0(t−π3B0α)cos60∘
=√32v0Baα+v02(t−π3B0α)
Topper's Solved these Questions
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Section B - Assertion Reasoning
31 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - AIPMTNEET Questions
47 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Magnetic Field Due To Circular Arc
69 Videos
- SEMICONDUCTOR ELECTRONICSBOOK - A2ZCHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - EXERCISE
29 Videos
- WAVE OPTICSBOOK - A2ZCHAPTER - WAVE OPTICSEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
Knowledge Check
The x -co- ordinates of the particle at time t (>π3B0α) would be
A−2V0B0αB−V0B0αC2V0B0αD−V0B0αA particle of charge per unit mass α is released from origin with velocity →v=v0ˆi in a magnetic field
→B=−B0ˆk for x≤√32v0B0α
and →B=0 for x>√32v0B0α
The x-coordinate of the particle at time t(>π3B0α) would beA√32v0B0α+√32v0(t−πB0α)B√32v0B0α+v0(t−π3B0α)C√32v0B0α+v02(t−π3B0α)D√32v0B0α+v0t2A particle of charge per unit mass α is released from origin with a velocity →v=v0ˆi uniform magnetic field →B=−B0ˆk. If the particle passes through (0,y,0), then y is equal to
A−2v0B0αBv0B0αC2v0B0αD−v0B0α
A particle of charge per unit mass α is released from origin with a velocity →v=v0ˆi in a magnetic field
→B=−B0ˆk for x≤√32v0B0α
and →B=0 for x>√32v0B0α
The x-coordinate of the particle at time t(π3B0α) would be
View SolutionA charged particle (q.m) released from origin with velocity v=v0ˆi in a uniform magnetic field B=B02ˆi+√3B02ˆJ.
Maximum z-coordinate of the particle is
View SolutionA charged particle (q.m) released from origin with velocity v=v0ˆi in a uniform magnetic field B=B02ˆi+√3B02ˆJ.
When z-co-ordinate has its maximum value
View SolutionA charged particle (q.m) released from origin with velocity v=v0ˆi in a uniform magnetic field B=B02ˆi+√3B02ˆJ.
Z-component of velocity is √3v02 after in t=……….
View SolutionAn electron is moving with an initial velocity →v=v0ˆi and is in a magnetic field →B=B0ˆj. Then it's de-Broglie wavelength
View Solution
