A particle of m1 moves in a circular path of radius R on a rotating .A string connecting the particles m1 and m2 passes over a smooth bole made on the table as shown in figure If mass m1 does not slide relative to the rotating table , mark the correct option as applicable.
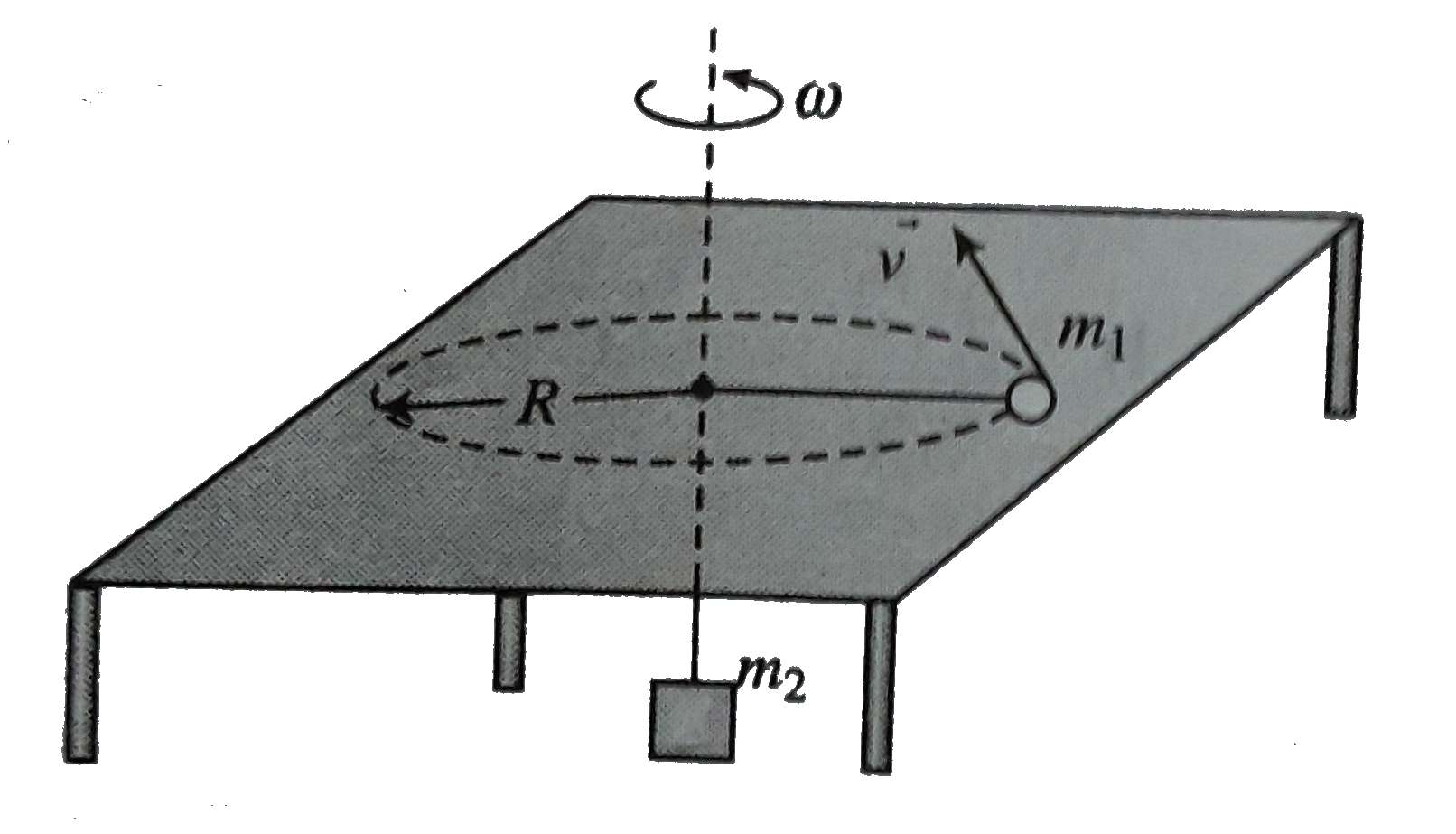
The friction force acting on the block m1is(m1ω2R−m2g) along radial rotation towards center of rotation
The friction force acting on the block m1is(m1ω2R−m2g) along tangle direction in the direction oppesite to→v
The maximum angular velocity of the particle is √(m2+μm1m1)gR
The minimum angular velocity of the particle is √(m2+μm1m1)gR
The correct Answer is:a,c,d
FBD Let the friction radially inward .The force on m1 are f←(assumed),T←N↑mtg↓ The force on m2 are m2g↓andT↑ as shown in figure
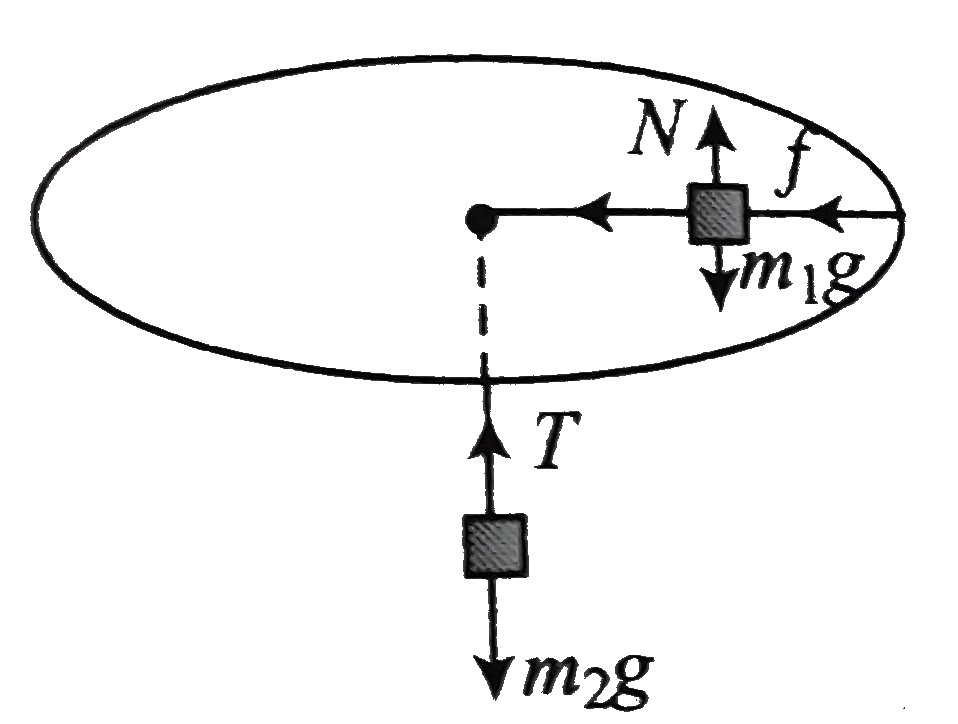 Force equation:
Force equation:
For m1:
∑Fy=N−m1g=maa1y (i)
∑Fr=f+T=m1ar (ii)
Fro m2:
∑Fy=T−m2g=m2a2y (iii)
Law of static friction:
f≤μN
Kinematics: a1y=0
ar=v2R
a2y=0 (vii)
Solving the above equations, we have
f=m1v2R−m2g or m1ω2R−mg
Now substituinh the above value of f and N in Eq (iv).
we have (m1v2R−m2g)≤μm1g
This gives vmax=√(m2+μm1m1)gR
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple Correct2videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Linked Comprehension52videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Subjective21videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
Similar Questions
A particle is moving on a circular path of radius 1 m with 2 m/s. If speed starts increasing at a rate of 2m/s2, then acceleration of particle is
View SolutionTwo blocks of mass m1andm2 lie on smooth horizontal table in contact with each other as shown in figure
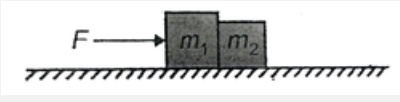
If a force F is applied to the mass m1 then the contact force between the block will beView Solution
Knowledge Check
- Question 1 - Select One
A particle moves in a circular path of radius 0.5 m with a linear speed of 2 ms−1 ,its angular speed is
A2rads−1B3rads−1C4rads−1DNone of these - Question 2 - Select One
A particle of mass m is moving on a circular path of radius r with uniform speed v , rate of change of linear momentum is
AZeroBIndependent of speedCProportional to radius rDProportional to v2 - Question 3 - Select One
A particle of mass m is rotating in a plane in circular path of radius r. Its angular momentum is L. The centripetal force acting on the particle is
Am2L2rBL2r2mCmLrDNone
A particle of mass 'm' is moving on a circular path of radius 'r' with uniform speed 'v'. Rate of change of linear momentum is
View SolutionA particle of mass m moves with constant speed v on a circular path of radius r as shown in figure. The average force on it during its motion from A to B is
 View Solution
View SolutionA Particle of mass 'M' moves in a uniform circular path of radius 'r' with a constant speed 'v' then its centripetal acceleration is .
View SolutionA particle of mass m is rotating in a plane in circular path of radius r. Its angular momentum is L. The centripetal force acting on the particle is
View SolutionIf a particle of mass 1 gm is moving along a circular path of radius 1 m with a velocity of 1 m/s, then the its angular momentum is
View Solution

