A particle of mass $1 k g$ is kept on the surface of a uniform sphere of mass $20 k g$ and radius $1.0 m$ . Find the work to be done against the gravitational force between them to take the particle away from the sphere.

Video Solution

Text Solution

Verified by Experts

(1) Because we have particles, the magnitude of the gravitational force on particel 1 due to either of the other particle is given by Eq. 13-1 $(F = G m_{1} m_{2} / r^{2})$ . (2) The direaction of either gravitational force on particle 1 is toward the particle responsible for it. (3) Because the forces are not along a single axis, we connot simply add or subtract their magnitudes or their components to get the net force. Instead,we must add them as vectors.
Calculations : From Eq. 13-1, the magnitude of the force ${\vec{F}}_{12}$ on particle 1 from particle 2 is
$F_{12} = \frac{G m_{1} m_{2}}{a^{2}}$
$= \frac{(6.67 \times 10^{- 11} m^{3} / K g . s^{2}) (6.0 k g) (4.0 K g)}{{(0.020 m)}^{2}}$
$4.00 \times 10^{- 6} N$ . (13-7)
Similartly, the magnitude of force ${\vec{F}}_{13}$ on particle 1 form particel 3 is
$F_{13} = \frac{G m_{1} m_{3}}{{(2 a)}^{2}}$
$= \frac{(6.67 \times 10^{- 11} m^{3} / K g . s^{2}) (6.0 k g) (4.0 k g)}{{(0.040 m)}^{2}}$
$= 1.00 \times 10^{- 6} N$ . (13-8)
Force ${\vec{F}}_{12}$ is directed in the positive direactionof the y axis (fig. 13-4b) and has only the y component $F_{12}$ . Similarly, ${\vec{F}}_{13}$ is direacted in the negative direaction of the x axis and has only the x component : We draw the force diagrams with the tail of a force vector anchored on the particel experiencing the force. Drawing them in other ways invites errors, especially on exams.)
To find the net force ${\vec{F}}_{1,net}$ on particle 1, we must add the two forces as vectors (figs 13-4d and e). We can do so no a vector-calculator. However, here we notes as vector -capable calculator. However, here we note that $- F_{13} and F_{12}$ are actually the x and y components of ${\vec{F}}_{1.net}$ . Therefore, we can use Eq. 3-6 to find first the magnitude and then the direaction of ${\vec{F}}_{1.net}$ . The magnitude is
$F_{1.net} = \sqrt{{(F_{12})}^{2} + {(- F_{13})}^{2}}$
$= \sqrt{{(4.00 \times 10^{- 6} N)}^{2} + {(- 1.00 \times 10^{- 6} N)}^{2}}$
$= 4.1 \times 10^{- 6} N$ .

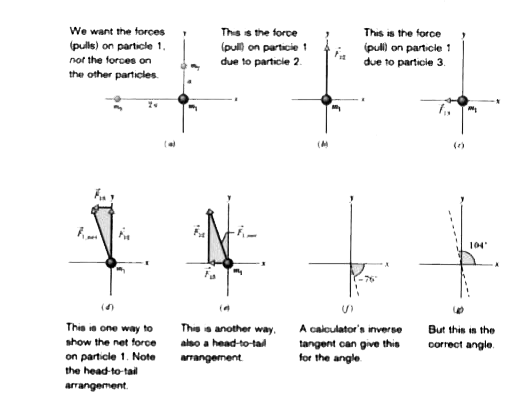
Figure 13-4 (a) An arrangement of three particle. The force on particle 1 due to (b) particel 2 and ( c) particle 3.(d)-(g) Ways to combine the forces to get the net force magnitude and orientation. In Wiley PLUS, this figure is avaliable as an animation with voiceover.
Relative to the positive direction of the x axis, Eq. 3-6 gives the direactionof ${\vec{F}}_{1.net}$ as
$θ = \tan^{- 1} \frac{F_{12}}{- F_{13}} = \tan^{- 1} \frac{4.00 \times 10^{- 6} N}{- 1.00 \times 10^{- 6} N} = - 76^{\circ}$ .
Is this a reasonable direaction (Fig.13-4F) ? No, because the direaction of ${\vec{F}}_{1.net}$ must be between the dreaction of ${\vec{F}}_{12} and {\vec{F}}_{13}$ . Recall from Chapter 2 that a calculator displays only one of the two possible answers to a $\tan^{- 1}$ funeton . We find the other answer by adding $180^{\circ}$ :
$- 76^{\circ} + 180^{\circ} = 104^{\circ}$ .
which is a reasonable direaction for ${\vec{F}}_{1.net}$ (Fig.13-4g).

Updated on:21/07/2023