A particle of mass and charge travelling with a velocity in the direction enters a region in which uniform electric field E and a uniform magnetic field of induction B are present such that The particle enters this region at time Determine the location (x,y,z coordinates) of the particle at If the electric field is switched off at this instant (with the magnetic field present), what will be the position of the particle at ?
net force acts o the particle long the +ve z-direction.
net force acts on the particle alog -ve z-direction
net force acting on particle is zero
net force acts in xy-plane
The correct Answer is:C
To solve the problem, we need to determine the position of the particle at two different times: first when both electric and magnetic fields are present, and then when only the magnetic field is present.
Step 1: Determine the forces acting on the particle
1. Electric Force (F_E): The electric force acting on the particle is given by:
FE=qE
where q=1.6×10−19C and Ez=−102.4×103V/m.
FE=(1.6×10−19)×(−102.4×103)=−1.6384×10−14N(in the -z direction)
2. Magnetic Force (F_B): The magnetic force acting on the particle is given by:
FB=q(v×B)
where v=(1.28×106,0,0)m/s and B=(0,8×10−2,0)T.
FB=q(vxBy)=(1.6×10−19)×(1.28×106)×(8×10−2)
FB=(1.6×10−19)×(1.28×106)×(0.08)=1.6384×10−14N(in the +z direction)
Step 2: Analyze the forces
Since FE and FB are equal in magnitude but opposite in direction, the net force on the particle is zero. Therefore, the particle will continue to move in the +x direction without any deflection.
Step 3: Calculate the position at t=5×10−6s
The position of the particle in the x-direction can be calculated using:
x=vx⋅t
Substituting the values:
x=(1.28×106)⋅(5×10−6)=6.4m
Since there is no motion in the y and z directions (as the forces cancel each other), we have:
y=0,z=0
Thus, the position of the particle at t=5×10−6s is:
(x,y,z)=(6.4,0,0)m
Step 4: Determine the position when the electric field is switched off
When the electric field is switched off, only the magnetic field is present. The particle will continue to move in the +x direction with the same velocity vx=1.28×106m/s.
Now we need to calculate the position at t=7.45×10−6s:
x=1.28×106⋅(7.45×10−6)=9.536m
Since there is still no motion in the y and z directions:
y=0,z=0
Thus, the position of the particle at t=7.45×10−6s is:
(x,y,z)=(9.536,0,0)m
Final Answer:
1. At t=5×10−6s: (x,y,z)=(6.4,0,0)m
2. At t=7.45×10−6s: (x,y,z)=(9.536,0,0)m
FE=qE
where q=1.6×10−19C and Ez=−102.4×103V/m.
FE=(1.6×10−19)×(−102.4×103)=−1.6384×10−14N(in the -z direction)
FB=q(v×B)
where v=(1.28×106,0,0)m/s and B=(0,8×10−2,0)T.
FB=q(vxBy)=(1.6×10−19)×(1.28×106)×(8×10−2)
FB=(1.6×10−19)×(1.28×106)×(0.08)=1.6384×10−14N(in the +z direction)
x=vx⋅t
Substituting the values:
x=(1.28×106)⋅(5×10−6)=6.4m
Since there is no motion in the y and z directions (as the forces cancel each other), we have:
y=0,z=0
(x,y,z)=(6.4,0,0)m
x=1.28×106⋅(7.45×10−6)=9.536m
Since there is still no motion in the y and z directions:
y=0,z=0
(x,y,z)=(9.536,0,0)m
1. At t=5×10−6s: (x,y,z)=(6.4,0,0)m
2. At t=7.45×10−6s: (x,y,z)=(9.536,0,0)m
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SCQ_TYPE5videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE1videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE1videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery59videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery1videos
MAGNETISM AND MATTER
Similar Questions
A particle of mass 2×10−3 kg, charge 4×10−3C enters in an electric field of 5V/m, then its kinetic energy after 10 s is
View SolutionA charge particle travels along a straight line with a speed v in region where both electric field E and magnetic field b are present.It follows that
View SolutionA proton of mass 1.67×10−27 kg and charge 1.6×10−19C is shot a uniform magnetic field, and perpendicular to the field with a velocity 5×106m/s. If the magnetic induction of the field is 1 tesla, find
(i) The radius of the circular pathView SolutionA particle of mass 1.6×10−27kg and charge 1.6×10−19 coulomb enters a uniform magnetic field of 1 Tesla as shown in the figure. The speed of the particle is 107m/s. The distance PQ will be
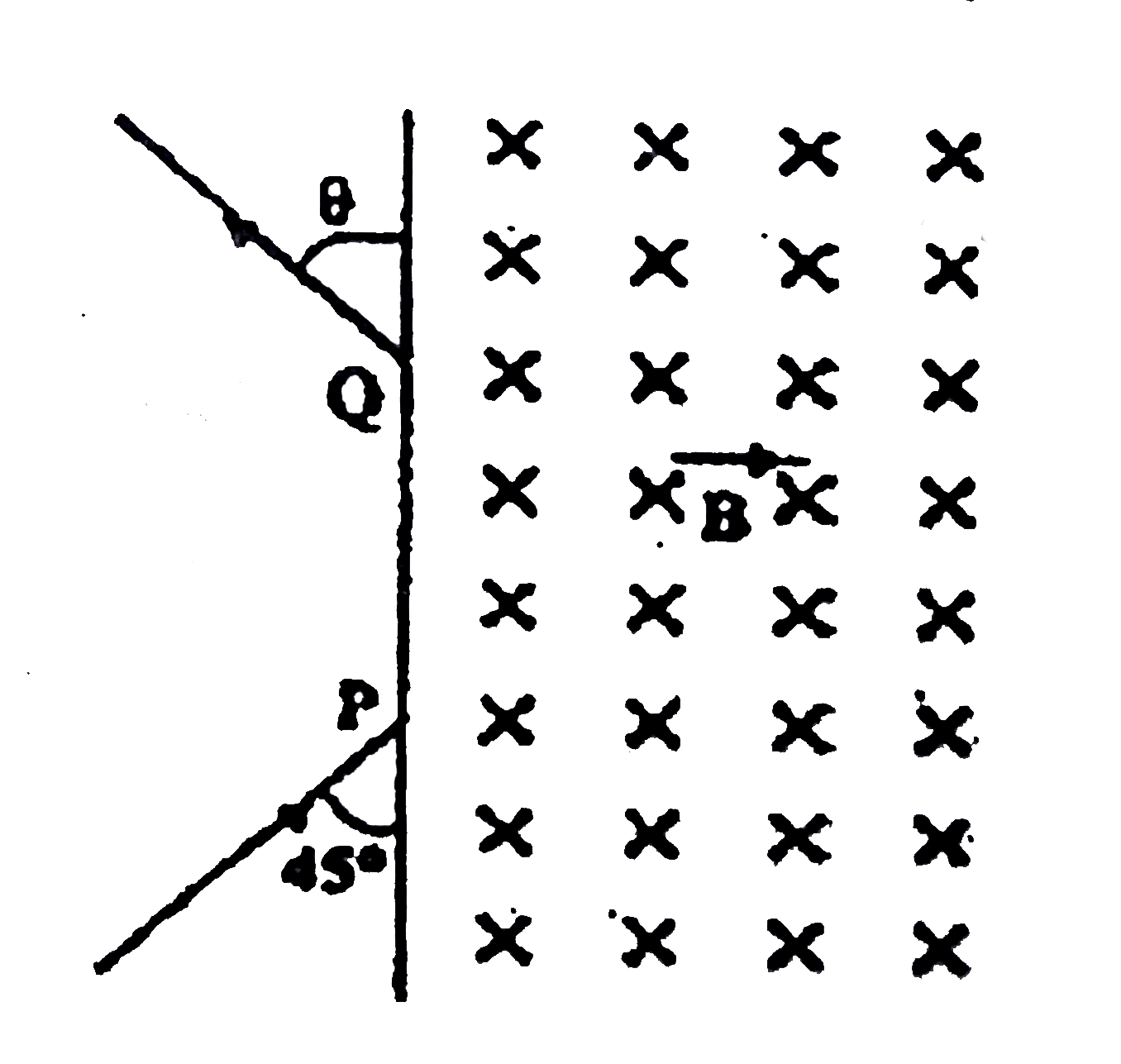 View Solution
View SolutionA particle of mass m=1.6X10−27 kg and charge q=1.6X10−19 C moves at a speed of 1.0X107ms−7. It enters a region of uniform magnetic field at a point E, as shown in The field has a strength of 1.0 T. (a) The magnetic field is directed into the plane of the paper. The particle leaves the region of the filed at the point F. Find the distance EF and the angle theta. (b) If the field is coming out of the paper, find the time spent by the particle in the regio the magnetic feld after entering it at E.
 View Solution
View SolutionA particle of mass 0.6g and having charge of 25nC is moving horizontally with a uniform velocity 1.2×104ms−1 in a uniform magnetic field, then the value of the magnetic induction is (g=10ms−2)
View SolutionA particle of mass 0.6g and having charge of 25nC is moving horizontally with a uniform velocity 1.2×104ms−1 in a uniform magnetic field, then the value of the magnetic induction is (g=10ms−2)
View SolutionIn a certain region, uniform electric field E=−E0ˆk and magnetic field B=B0ˆk are present. At time t=0, a particle of mass m and charge q is given a velocity v=vj+vk. Find the minimum speed of the particle and the time when it happens so.
 View Solution
View SolutionA particle of charge −16×10−18 coulomb moving with velocity 10ms−1 along the x− axis , and an electric field of magnitude 104/(m) is along the negative z− axis. If the charged particle continues moving along the x- axis , the magnitude of B is
View SolutionA particle of mass m and charge Q moving with a velocity v enters a region on uniform field of induction B Then its path in the region is s
View Solution

