Two circular coils A and B of radius 5√2cm amd 5cm respectively current 5amp and 5√2Amp respectively The plane of B is perpendicular to plane of A their centres coincide Find the magnetic field at the centre .
0
4π√2×10−5T
4π×10−5T
2π√2×10−5T
The correct Answer is:C
To find the magnetic field at the center of two circular coils A and B, we will follow these steps:
Step 1: Identify the given values
- Radius of coil A, r1=5√2 cm = 5√2×10−2 m
- Radius of coil B, r2=5 cm = 5×10−2 m
- Current in coil A, I1=5 A
- Current in coil B, I2=5√2 A
- The angle between the planes of the coils, θ=90∘
Step 2: Calculate the magnetic field due to coil A at the center
The formula for the magnetic field at the center of a circular coil is given by:
B=μ0I2R
where μ0=4π×10−7T m/A.
For coil A:
B1=4π×10−7×52×(5√2×10−2)
Calculating B1:
B1=4π×10−7×52×5√2×10−2=4π×10−7×5√210×10−2=2√2π×10−5T
Step 3: Calculate the magnetic field due to coil B at the center
For coil B:
B2=4π×10−7×5√22×(5×10−2)
Calculating B2:
B2=4π×10−7×5√210×10−2=4π×10−7×510√2×10−2=2√2π×10−5T
Step 4: Determine the resultant magnetic field
Since the magnetic fields B1 and B2 are perpendicular to each other, we can use the Pythagorean theorem to find the resultant magnetic field B:
B=√B21+B22
Substituting the values:
B=√(2√2π×10−5)2+(2√2π×10−5)2
B=√2×(2√2π×10−5)2=2√2π×10−5√2
B=4π×10−5T
Final Answer
The resultant magnetic field at the center is:
B=4π×10−5T
- Radius of coil A, r1=5√2 cm = 5√2×10−2 m
- Radius of coil B, r2=5 cm = 5×10−2 m
- Current in coil A, I1=5 A
- Current in coil B, I2=5√2 A
- The angle between the planes of the coils, θ=90∘
The formula for the magnetic field at the center of a circular coil is given by:
B=μ0I2R
where μ0=4π×10−7T m/A.
B1=4π×10−7×52×(5√2×10−2)
B1=4π×10−7×52×5√2×10−2=4π×10−7×5√210×10−2=2√2π×10−5T
For coil B:
B2=4π×10−7×5√22×(5×10−2)
B2=4π×10−7×5√210×10−2=4π×10−7×510√2×10−2=2√2π×10−5T
Since the magnetic fields B1 and B2 are perpendicular to each other, we can use the Pythagorean theorem to find the resultant magnetic field B:
B=√B21+B22
Substituting the values:
B=√(2√2π×10−5)2+(2√2π×10−5)2
B=√2×(2√2π×10−5)2=2√2π×10−5√2
B=4π×10−5T
The resultant magnetic field at the center is:
B=4π×10−5T
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SCQ_TYPE5videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE1videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE1videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery59videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery1videos
MAGNETISM AND MATTER
Similar Questions
Two circular coils of radii 5cm and 10cm carry currents of 2A. The coils have 50 and 100 turns respectiely and are placed in such a way that their planes as well as their cetre coincide. Magnitude of magnetic field at the common centre of coils is
View SolutionTwo concentric coplaner circular loops of radii r1 and r2 carry currents of respectively i1 and i2 in opposite directions (one clockwise and the other anticlockwise .) The magnetic induction at the centre of the loops is half that due to i1 alone at the centre . If r2=2r , the value of i2/i1 is
View SolutionTwo circular coils of radii 5.0 cm and 10 cm carry equal currents of 2.0 A. The coils have 50 and 100 turns respectively and are placed in such a way that their planes as well as the centres coincide. Find the magnitude of the magnetic field B at the common centre of the coils if the currents in the coils are (a) in the same sense (b) in the opposite sense.
View SolutionA circular coil of radius 1⋅5cmcarriesacurrentof1⋅5A. If the coil has 25 turns , find the magnetic field at the centre.
View SolutionA semicircular wire of radius 5.0 cm carries a current of 5.0 A. A magnetic field B of magnitude 0.50 T exists along the perpendicular to the plane of the wire. Find the magnitude of the magnetic force acting on the wire.
View SolutionTwo identical circular wires P and Q each of radius R and carrying current 'I' are kept in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.
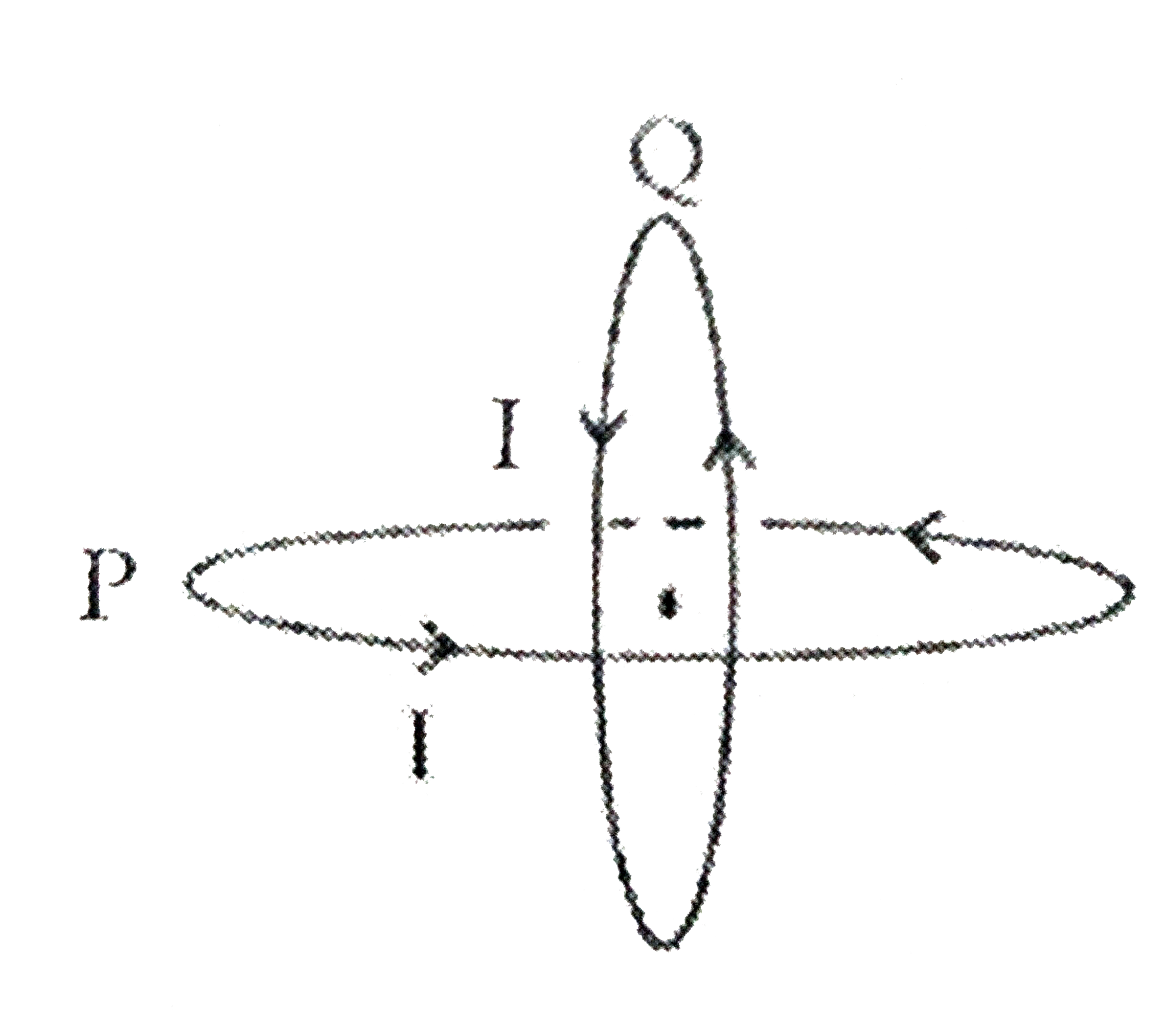 View Solution
View SolutionAn electron makes (3×105) revolutions per second in a circle of radius 0.5 angstrom. Find the magnetic field B at the centre of the circle.
View SolutionTwo circular coils of radii 5.0 cm and 10 cm carry equal currents of 2.0 A. The coils have 50 and 100 turns respectively and are placed in such a way that their planes are perpendicular to each other, what would be the magnitude of the magnetic field B at the centre ?
View SolutionIn the given figure find out magnetic field at point B (Given : I=2.5A, r=5cm)
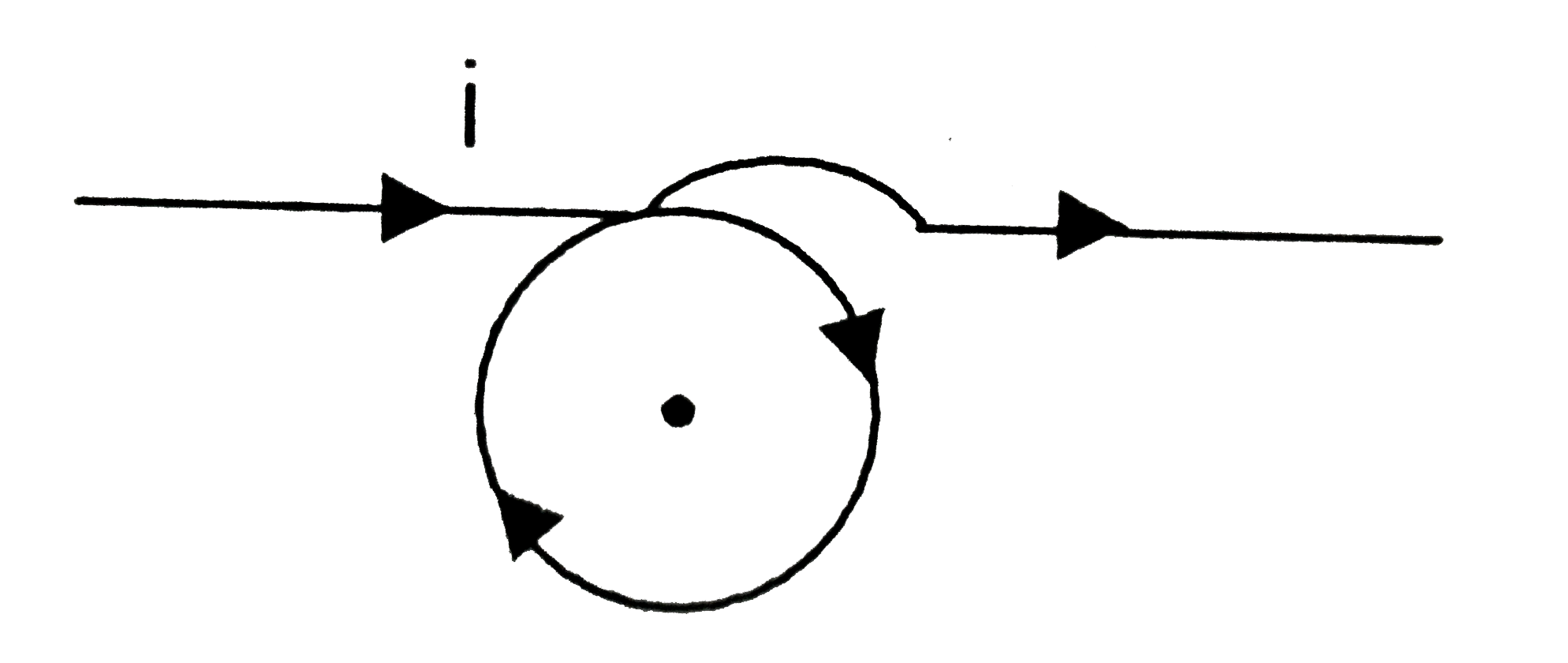 View Solution
View SolutionA 2A current is flowing through a circular coil of radius 10 cm containing 100 turns. Find the magnetic flux density at the centre of the coil.
View Solution

