A particle of mass m and charge q is projected into a region having a perpendicular magnetic, field B. Find the angle of deviation of the particle as it comes out of the magnetic field if the, width of the region is b, which is very slightly less than mv2Bq
To solve the problem, we will follow these steps:
Step 1: Understand the motion of the charged particle in a magnetic field
When a charged particle moves through a magnetic field, it experiences a magnetic force that acts perpendicular to both the velocity of the particle and the magnetic field. This results in circular motion.
Step 2: Determine the radius of the circular path
The radius r of the circular path of a charged particle in a magnetic field is given by the formula:
r=mvqB
where:
- m is the mass of the particle,
- v is the velocity of the particle,
- q is the charge of the particle,
- B is the magnetic field strength.
Step 3: Relate the angle of deviation to the geometry of the motion
As the particle enters and exits the magnetic field, it deviates from its original path. The angle of deviation θ can be related to the distance d traveled in the magnetic field and the radius r of the circular path. The sine of the angle of deviation is given by:
sinθ=dr
Step 4: Substitute the expression for radius into the sine formula
Substituting the expression for r into the sine formula gives:
sinθ=dmvqB=qBdmv
Step 5: Solve for the angle of deviation
Now, we can find the angle θ by taking the inverse sine:
θ=sin−1(qBdmv)
Step 6: Consider the width of the region
Given that the width b of the region is very slightly less than mv2B, we can substitute d=b into the equation for θ:
θ=sin−1(qBbmv)
Final Expression for Angle of Deviation
Thus, the angle of deviation of the particle as it comes out of the magnetic field is:
θ=sin−1(qBbmv)
When a charged particle moves through a magnetic field, it experiences a magnetic force that acts perpendicular to both the velocity of the particle and the magnetic field. This results in circular motion.
The radius r of the circular path of a charged particle in a magnetic field is given by the formula:
r=mvqB
where:
- m is the mass of the particle,
- v is the velocity of the particle,
- q is the charge of the particle,
- B is the magnetic field strength.
As the particle enters and exits the magnetic field, it deviates from its original path. The angle of deviation θ can be related to the distance d traveled in the magnetic field and the radius r of the circular path. The sine of the angle of deviation is given by:
sinθ=dr
Substituting the expression for r into the sine formula gives:
sinθ=dmvqB=qBdmv
Now, we can find the angle θ by taking the inverse sine:
θ=sin−1(qBdmv)
Given that the width b of the region is very slightly less than mv2B, we can substitute d=b into the equation for θ:
θ=sin−1(qBbmv)
Thus, the angle of deviation of the particle as it comes out of the magnetic field is:
θ=sin−1(qBbmv)
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SCQ_TYPE
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE
1 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
Similar Questions
A particle of mass m and charge q is projected into a region having a perpendicular magnetic field B. Find the angle of deviation of the particle as it comes out of the magnetic field if ihe width d of the region is
2mvqB

View SolutionA particle of mass m and charge q is projected into a region having a perpendicular magnetic field B. Find the angle of deviation fo the particle as it comes out of the magnetic field if the width d of the regions is very smaller then

View SolutionA particle of mass m and charge q is projected into a region having a perpendicular magnetic field B. Find the angle of deviation fo the particle as it comes out of the magnetic field if the width d of the regions is very smaller then

View SolutionA charged particle of mass m and charge q travels on a circular path of radius r that is perpendicular to a magnetic field B. The time takeen by the particle to complete one revolution is
View SolutionA charged particle (q,m) enters perpendicular in a uniform magnetic field B and comes out field as shown. Find the angle of deviation θ for particle to cross magnetic field will be
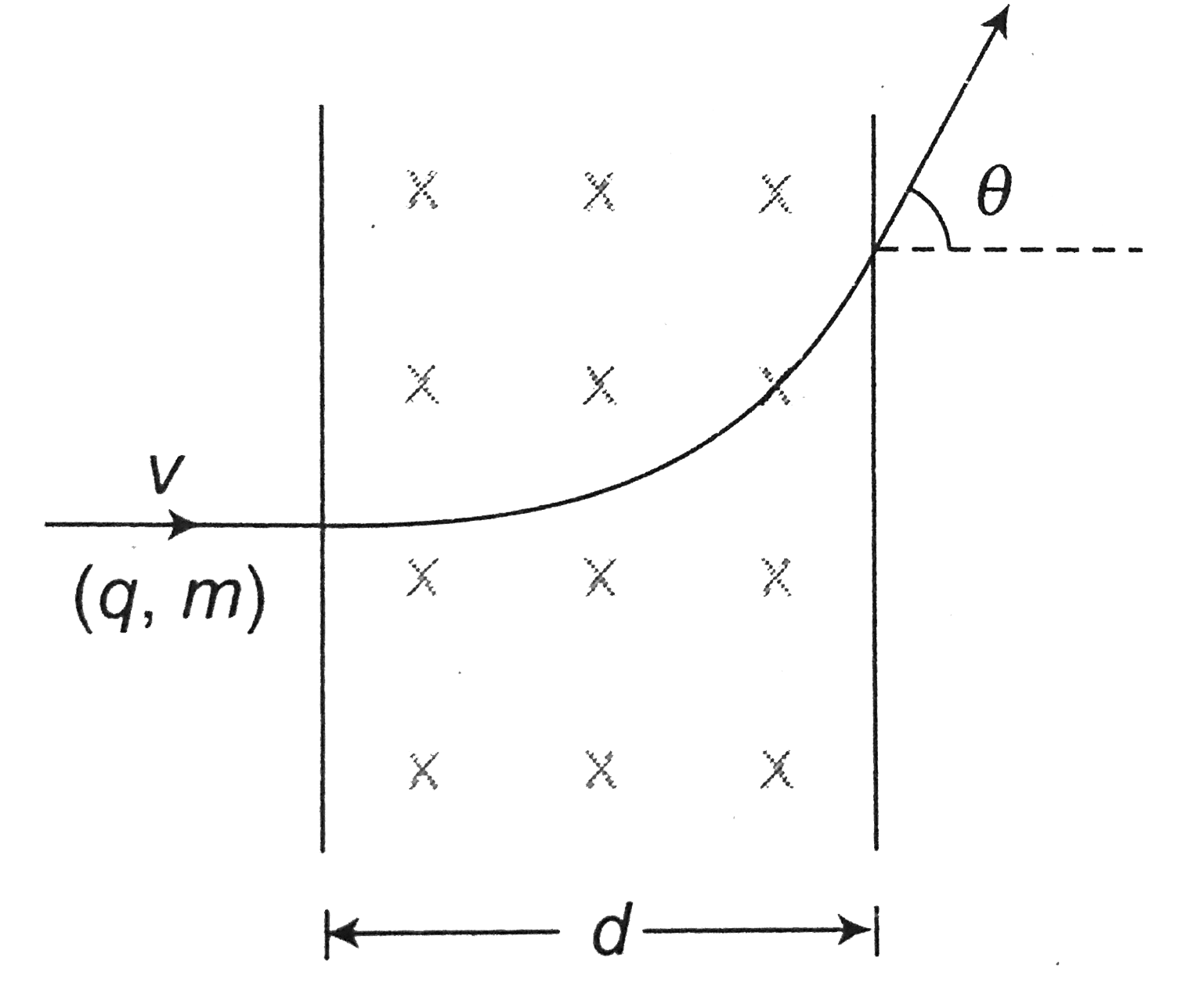
View SolutionA particle of mass m and charge q is thrown in a region where uniform gravitational field and electric field are present. The path of particle:
View SolutionIf a charged particle goes unaccelerated in a region containing electric and magnetic fields,
View SolutionIf a charged particle goes unaccelerated in a region containing electric and magnetic fields,
View SolutionA charged particle of mass m and charge q describes circular motion of radius r in a uniform magnetic field of strength B the frequency of revolution is
View SolutionA charged particle of mass m and charge q is projected into a uniform magnetic field of induciton →B with speed v which is perpendicular to →B. The width of the magnetic field is d. The impulse imparted to the particle by the field is (d<<mv/qB)
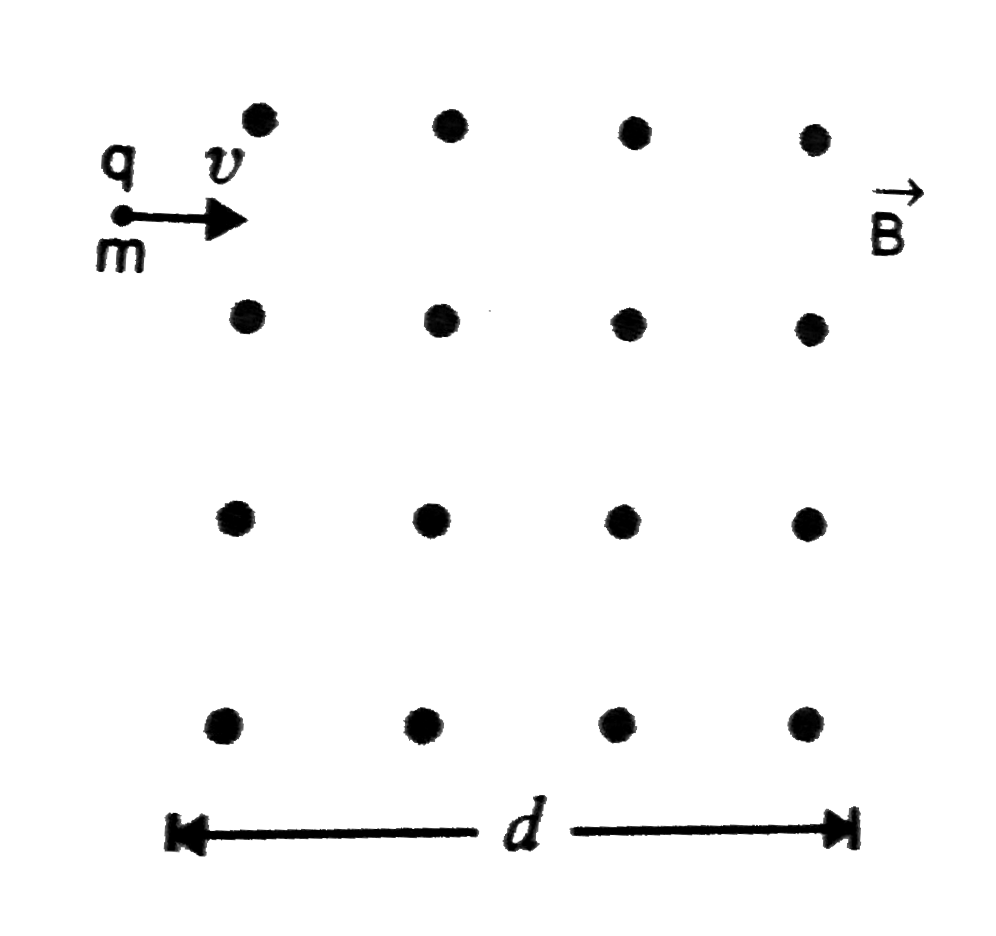
View Solution
