A particle of mass carrying charge is projected with velocity from point toward aninfinite line of charge from a distance . Its speed reduces to zero momentarily at point , which is at a distance from the line of charge. If another particle with mass and charge is projected with the same velosity from toward the line of charge, what will be its speed at ?
The correct Answer is:a
To solve the problem, we will use the principle of conservation of energy. Here are the steps to find the speed of the second particle at point Q.
Step 1: Understand the scenario
We have two particles:
1. Particle 1: Mass = m, Charge = q, Initial velocity = v, projected from point P at a distance a from an infinite line of charge.
2. Particle 2: Mass = m, Charge = -q, also projected from point P with the same initial velocity v.
Both particles are projected towards the line of charge, and we need to find the speed of the second particle at point Q, which is at a distance a2 from the line of charge.
Step 2: Apply conservation of energy for Particle 1
For Particle 1, the change in potential energy (PE) and kinetic energy (KE) can be expressed as follows:
- Initial kinetic energy at point P:
KEinitial=12mv2
- Potential energy at point P (distance a from the line of charge):
PEinitial=kq⋅Qa(where Q is the linear charge density)
- Potential energy at point Q (distance a2 from the line of charge):
PEfinal=kq⋅Qa2=2kq⋅Qa
Using conservation of energy:
KEinitial+PEinitial=KEfinal+PEfinal
Substituting the values:
12mv2+kq⋅Qa=0+2kq⋅Qa
Step 3: Solve for Particle 1
Rearranging the equation gives:
12mv2=2kq⋅Qa−kq⋅Qa
12mv2=kq⋅Qa
Step 4: Apply conservation of energy for Particle 2
For Particle 2, we will use the same approach:
- Initial kinetic energy at point P:
KEinitial=12mv2
- Potential energy at point P:
PEinitial=k−q⋅Qa
- Potential energy at point Q:
PEfinal=k−q⋅Qa2=−2kq⋅Qa
Using conservation of energy:
KEinitial+PEinitial=KEfinal+PEfinal
Substituting the values:
12mv2+k−q⋅Qa=KEfinal+(−2kq⋅Qa)
Step 5: Solve for Particle 2
Rearranging gives:
12mv2+kq⋅Qa=KEfinal
Substituting kq⋅Qa from Particle 1:
KEfinal=12mv2+kq⋅Qa
From Particle 1, we know:
kq⋅Qa=12mv2
Thus:
KEfinal=12mv2+12mv2=mv2
Step 6: Find the final speed V1
Since KEfinal=12mV21:
mv2=12mV21
V21=2v2
V1=√2v
Final Answer
The speed of the second particle at point Q is:
V1=√2v
We have two particles:
1. Particle 1: Mass = m, Charge = q, Initial velocity = v, projected from point P at a distance a from an infinite line of charge.
2. Particle 2: Mass = m, Charge = -q, also projected from point P with the same initial velocity v.
For Particle 1, the change in potential energy (PE) and kinetic energy (KE) can be expressed as follows:
- Initial kinetic energy at point P:
KEinitial=12mv2
- Potential energy at point P (distance a from the line of charge):
PEinitial=kq⋅Qa(where Q is the linear charge density)
- Potential energy at point Q (distance a2 from the line of charge):
PEfinal=kq⋅Qa2=2kq⋅Qa
KEinitial+PEinitial=KEfinal+PEfinal
Substituting the values:
12mv2+kq⋅Qa=0+2kq⋅Qa
Rearranging the equation gives:
12mv2=2kq⋅Qa−kq⋅Qa
12mv2=kq⋅Qa
For Particle 2, we will use the same approach:
- Initial kinetic energy at point P:
KEinitial=12mv2
- Potential energy at point P:
PEinitial=k−q⋅Qa
- Potential energy at point Q:
PEfinal=k−q⋅Qa2=−2kq⋅Qa
KEinitial+PEinitial=KEfinal+PEfinal
Substituting the values:
12mv2+k−q⋅Qa=KEfinal+(−2kq⋅Qa)
Rearranging gives:
12mv2+kq⋅Qa=KEfinal
Substituting kq⋅Qa from Particle 1:
KEfinal=12mv2+kq⋅Qa
From Particle 1, we know:
kq⋅Qa=12mv2
Thus:
KEfinal=12mv2+12mv2=mv2
Since KEfinal=12mV21:
mv2=12mV21
V21=2v2
V1=√2v
The speed of the second particle at point Q is:
V1=√2v
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Multiple Correct
10 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Comprehension
31 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Subjective
28 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
A particle of charge q is projected from point P with velocity v as shown. Choose the correct statement from the following.

View SolutionA charge particle of mass m and charge q is projected with velocity v along y-axis at t=0.

Find the velocity vector and position vector of the particle →v(t)and→r(t) in relation with time.
View SolutionA charge particle of mass m and charge q is released from rest in uniform electric field. Its graph between velocity (v) and distance travelled (x) will be :
View SolutionA charge particle of mass m and charge q is released from rest in uniform electric field. Its graph between velocity (v) and distance travelled (x) will be :
View SolutionTwo point charges, each of mass m and charge q are released when they are at a distance d from each other. What is the speed of each charged particle when they are at a distance 2r ?
View SolutionA charge particle of mass m and charge q is projected with velocity v along plane a distance a from a long straight current carrying conductor as shown in figure. The radius of curvature of the path traced by the particle at the given position does not depend on

View SolutionA positive charge particle of mass m and charge q is projected with velocity v as shown in Fig. If radius of curvature of charge particle in magnetic field region is greater than d, then find the time spent by the charge particle in magnetic field.
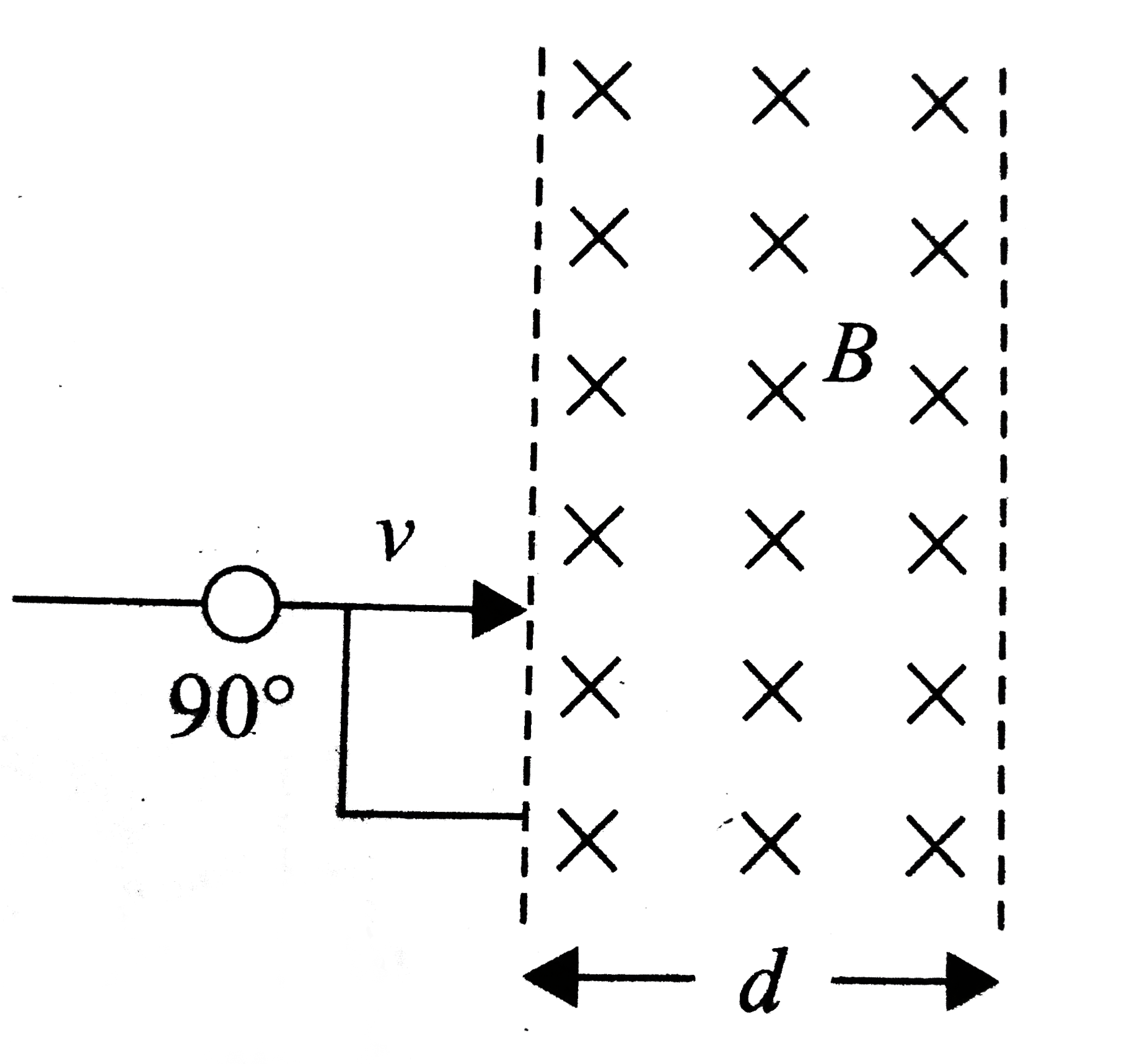
View SolutionA particle of mass m and charge −q is projected from the origin with a horizontal speed v into an electric field of intensity E directed downward. Choose the wrong statement. Neglect gravity

View SolutionA particle of mass m and charge −q is projected from the origin with a horizontal speed v into an electric field of intensity E directed downward. Choose the wrong statement. Neglect gravity

View SolutionA particle of mass m carrying charge '+q1' is revolving around a fixed charge '−q2' in a circular path of radius r. Calculate the period of revolution.
View Solution
