A charge particle of mass m and charge q is released from rest in uniform electric field. Its graph between velocity (v) and distance travelled (x) will be :

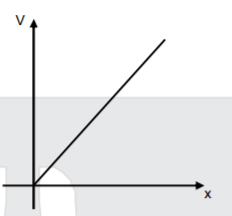
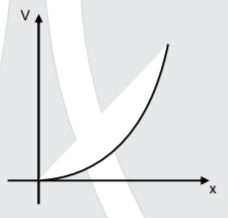
The correct Answer is:A
To solve the problem of a charged particle of mass m and charge q released from rest in a uniform electric field, we need to derive the relationship between the velocity v of the particle and the distance x it travels.
1. Identify the Force on the Charged Particle:
The force F acting on the charged particle in an electric field E is given by:
F=qE
2. Apply Newton's Second Law:
According to Newton's second law, the force is also equal to the mass times acceleration:
F=ma
Therefore, we can equate the two expressions for force:
ma=qE
From this, we can express the acceleration a as:
a=qEm
3. Relate Acceleration to Velocity and Distance:
We know that acceleration can also be expressed as the derivative of velocity with respect to time:
a=dvdt
We can also express a in terms of velocity and distance:
a=vdvdx
Setting these equal gives us:
vdvdx=qEm
4. Separate Variables and Integrate:
Rearranging the equation, we have:
vdv=qEmdx
Now, we can integrate both sides. The left side integrates from 0 to v and the right side from 0 to x:
∫v0vdv=∫x0qEmdx
The integral of v gives:
v22∣∣∣v0=qEmx∣∣∣x0
This results in:
v22=qEmx
5. Rearranging the Equation:
Multiplying both sides by 2 gives:
v2=2qEmx
6. Identifying the Graph:
The equation v2=2qEmx is in the form of y=kx, where y=v2 and k=2qEm. This indicates that the graph of v2 against x is a straight line, and since v is the square root of v2, the graph of v against x will be a parabola opening to the right.
Conclusion:
The graph between velocity v and distance x will be a parabola symmetric about the x-axis.
---
The force F acting on the charged particle in an electric field E is given by:
F=qE
According to Newton's second law, the force is also equal to the mass times acceleration:
F=ma
Therefore, we can equate the two expressions for force:
ma=qE
From this, we can express the acceleration a as:
a=qEm
We know that acceleration can also be expressed as the derivative of velocity with respect to time:
a=dvdt
We can also express a in terms of velocity and distance:
a=vdvdx
Setting these equal gives us:
vdvdx=qEm
Rearranging the equation, we have:
vdv=qEmdx
Now, we can integrate both sides. The left side integrates from 0 to v and the right side from 0 to x:
∫v0vdv=∫x0qEmdx
The integral of v gives:
v22∣∣∣v0=qEmx∣∣∣x0
This results in:
v22=qEmx
Multiplying both sides by 2 gives:
v2=2qEmx
The equation v2=2qEmx is in the form of y=kx, where y=v2 and k=2qEm. This indicates that the graph of v2 against x is a straight line, and since v is the square root of v2, the graph of v against x will be a parabola opening to the right.
The graph between velocity v and distance x will be a parabola symmetric about the x-axis.
Topper's Solved these Questions
Similar Questions
A particle of mass m and charge −q is released from rest in a uniform electric field. If there is no other force on the particle, the dependence of its potential energy on the distance x travelled by it is correctly given by (assume initial potential energy to be zero ,graphs are schematic and not drawn to scale)
View SolutionA particle of mass m and charge −q is released from rest in a uniform electric field. If there is no other force on the particle, the dependence of its potential energy on the distance x travelled by it is correctly given by (assume initial potential energy to be zero ,graphs are schematic and not drawn to scale)
View SolutionA charge of mass .m. charge .2e. is released from rest in a uniform electric field of strength .E.. The time taken by it to travel a distance .d. in the field is
View SolutionA particle of mass and charge is released from rest in a uniform electric field. If there is no other force on the particle, the dependence of its kinetic energy on the distance travelled by it is correctly given by (graphs are schematic and not drawn to scale)
View SolutionA particle of mass and charge is released from rest in a uniform electric field. If there is no other force on the particle, the dependence of its kinetic energy on the distance travelled by it is correctly given by (graphs are schematic and not drawn to scale)
View SolutionA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View SolutionA particle of mass m and charge q is released from rest in uniform electric field of intensity E. Calculate the kinetic energy it attains after moving a distance y between the plates.
View SolutionA charged particle of mass m and charge q is released from rest the position (x0,0) in a uniform electric field E0ˆj. The angular momentum of the particle about origin.
View SolutionA particle of mass ma and charge q is released from rest in a uniform filed of magnitude E. the uniform field is created between two parallel plates of charge densities +σ and −σ, respectively. The particle accelerates toward the other plate a distance d apart. Determine the speed at which it stirkes the opposite plate.

View SolutionA particle of mass m and charge q is placed at rest in a uniform electric field E and then released, the kinetic energy attained by the particle after moving a distance y will be
View Solution