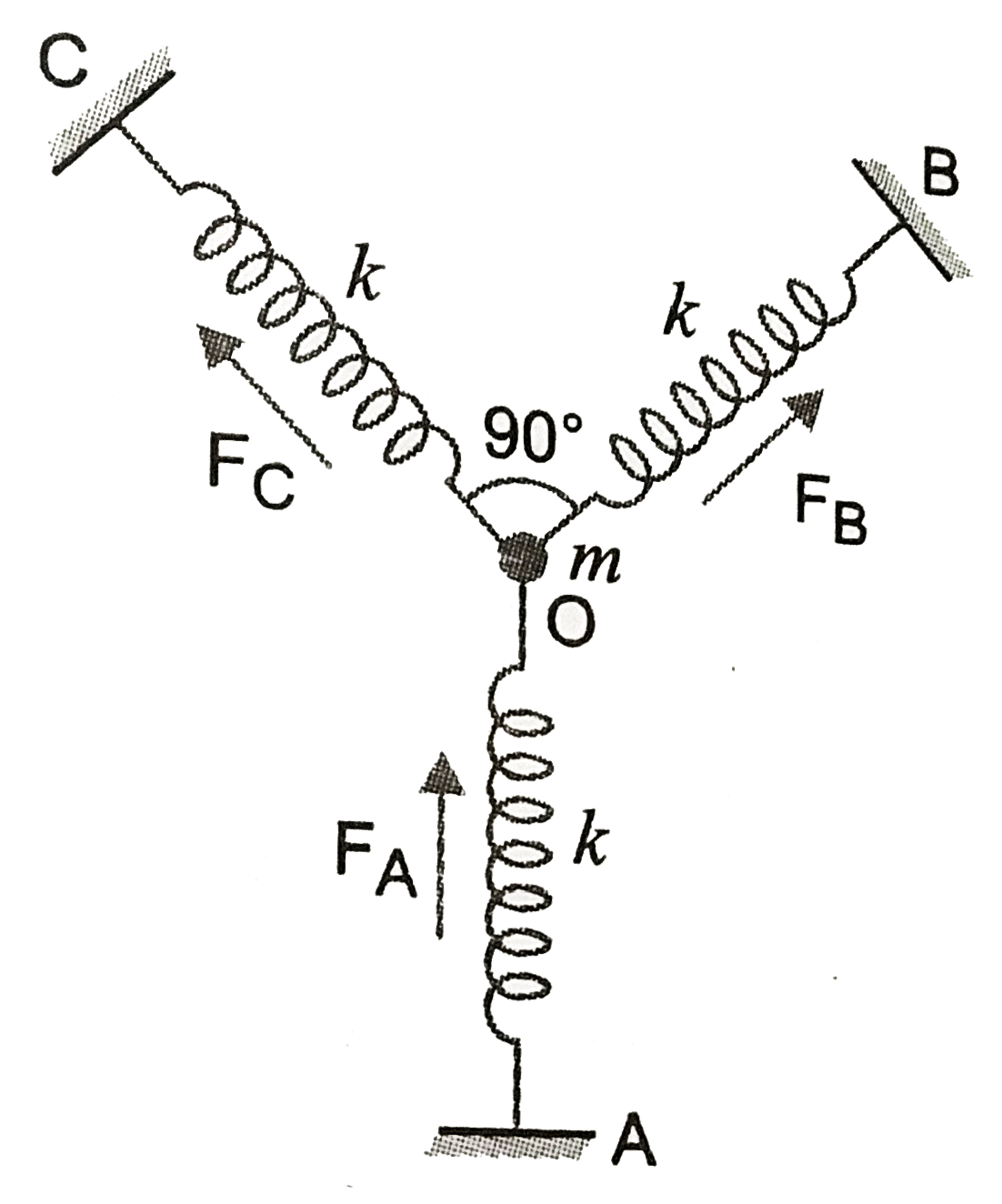
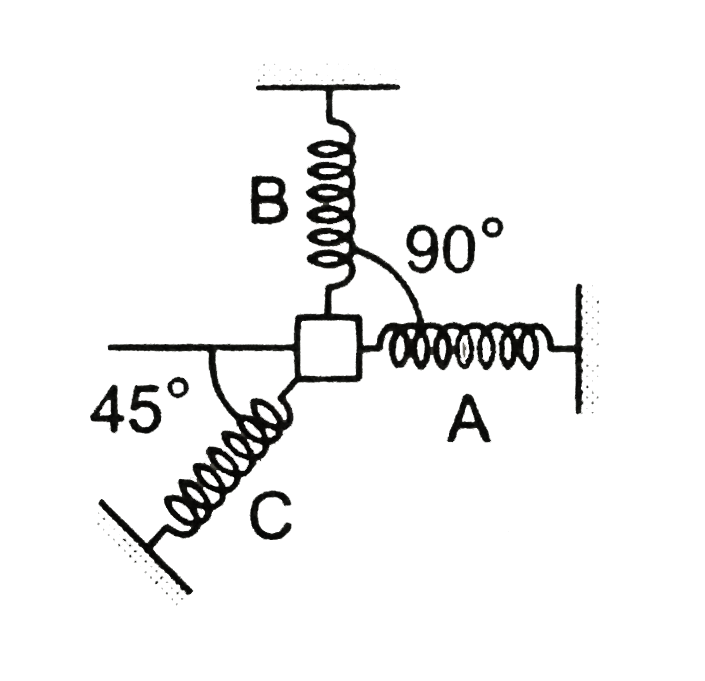
A particle of mass is attached to three identical springs of spring constant as shwon in figure. The time period of vertical oscillation of the particle is

The correct Answer is:B
When the particle of mass is pushed by distance in the direction of ,the spring will be compressed by , while spring and each will be stretched by , Total restoring force on the mass along is
or ...(i)
As and is directed towards the equilibrium position . Hence mass if left free, will execute lkinear SHM. Comparing (i) with , we find that
Spring factor,
Here, inertia factor mass of particle
Time period,
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:integer type question
Explore 8 Videos
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:Assertion-Reason Type Questions
Explore 23 Videos
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:Multiple Choice Question-II
Explore 14 Videos
- MATHEMATICAL TOOLSBook:PRADEEPChapter:MATHEMATICAL TOOLSExercise:Fill in the blanks
Explore 5 Videos
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:Competiton Focus Jee Medical Entrance
Explore 18 Videos
Similar Questions
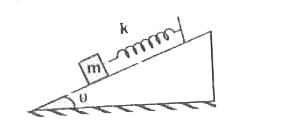
A block of mass m can slide along a frictionless inclined plane, is attached to a ideal spring of spring constant as shown in the figure. Find the period of its oscillation. (Frame of reference attached to the wedge is at rest)
View SolutionA particle of mass m is attached with three springs A,B and C of equal force constancts k as shown in figure. The particle is pushed slightly against the spring C and released. Find the time period of oscillation.
 .
.
View Solution
Knowledge Check
A particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mkA particle of mass 'm' is attached to three identical springs A,B and C each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is
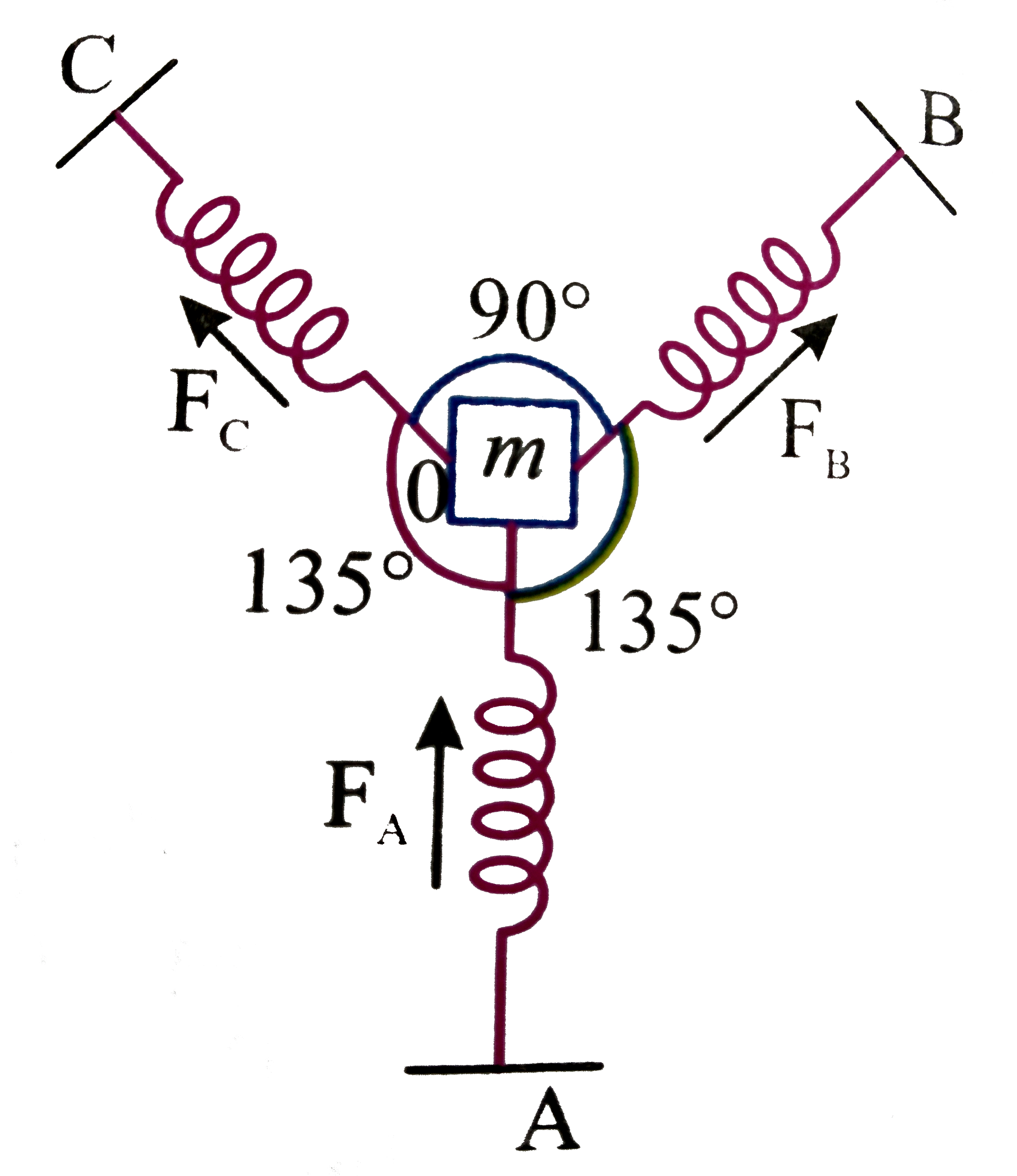 AT=2π√mKBT=2π√2mKCT=2π√m2KDT=π√mK
AT=2π√mKBT=2π√2mKCT=2π√m2KDT=π√mKThe following figure shows a particle of mass, m, attached with four identical springs, each of length l. Initial tension in each spring is F0. The period of small oscillations of the particle along a line perpendicular to the plane of the figure is (neglect gravity)
 Aπ√mlF0B2π√mlF0C2π√ml2F0Dπ√ml4F0
Aπ√mlF0B2π√mlF0C2π√ml2F0Dπ√ml4F0
A particle of mass m is asttached to three springs A,B and C of equla force constants k as shown in figure. If the particle is pushed slightly against the spring C and released, find the time period of oscillastion.
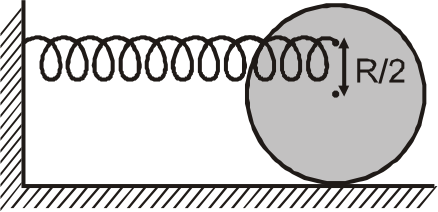
View SolutionA uniform disc of mass m is attached to a spring of spring constant k as shown in figure and there is sufficient friction to prevent slipping of disc. Time period of small oscillations of disc is:
View SolutionA mass m is suspended from a spring of force constant k and just touches another idential spring fixed to the floras shown in the figure. The time period of small oscillation is
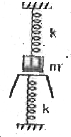
View Solution
A mass m is suspended from a spring of force constant k and just touches another identical spring fixed to the floor as shown in the fig. The time period of small oscillations is
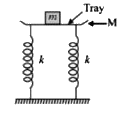
View SolutionA tray of mass M = 10 kg executes SHM of period 1.5s. It is supported on two identical springs of spring constant k as shown in figure. If a block of mass m is also placed on the tray, the period of oscillation increases to 3s. The value of m is:
View Solution