A particle of mass m is initially situated at point P inside a hemispherical surface of radius r as shown in the figure. A horizontal acceleration of magnitude ao is suddenly produced acceleration on the particle in the horizontal direction. If gravitational acceleration is neglected, then time taken by the particle to touch the sphere again is

√4rsinαao
√4rtanαao
√4rcosαao
None of these
The correct Answer is:(c )
s = 2r cos α
since = s = 12a0t2 or 2rcosα=12a0t2
theefore = √4rcosαa0

Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT EXEMPLAR PROBLEMS
6 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSERTION AND REASON
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - RELATIVE VELOCITY
18 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
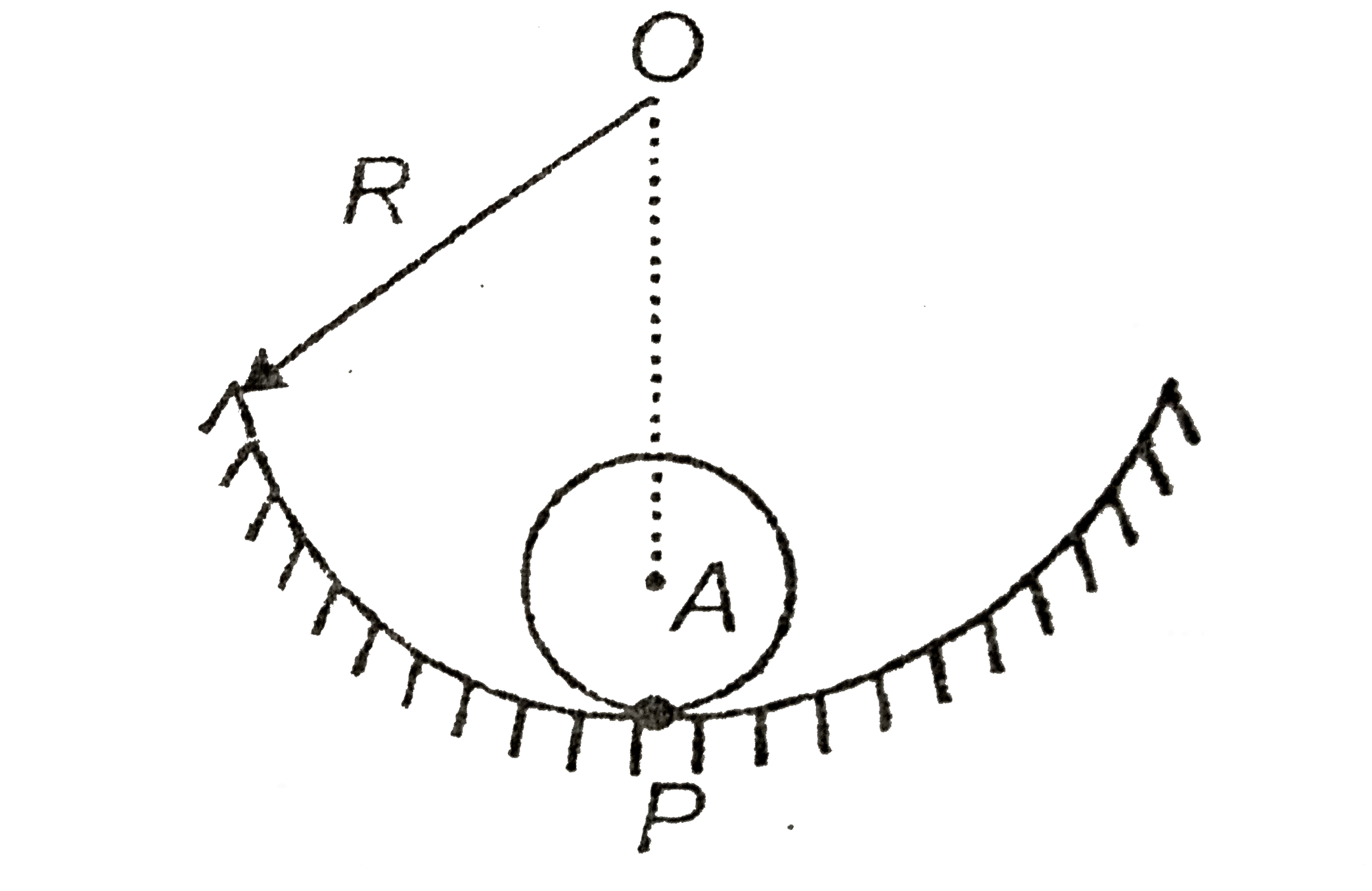
A sphere of radius r is rolling without slipping on a hemispherical surface of radius R. Angular velocity and angular acceleration of line OA is ω and α respectively. Find the acceleration of point P on sphere.
View SolutionA particle of mass m is thrown horizontally from the top of a tower and anoher particle of mass 2m is thrown vertically upward. The acceleration of centre of mass is
View SolutionA particle of mass m is thrown horizontally from the top of a tower and anoher particle of mass 2m is thrown vertically upward. The acceleration of centre of mass is
View SolutionInitial velocity and acceleration of a particles are as shown in the figure. Acceleration vector of particle remain constant. Then radius of curvature of path of particle :
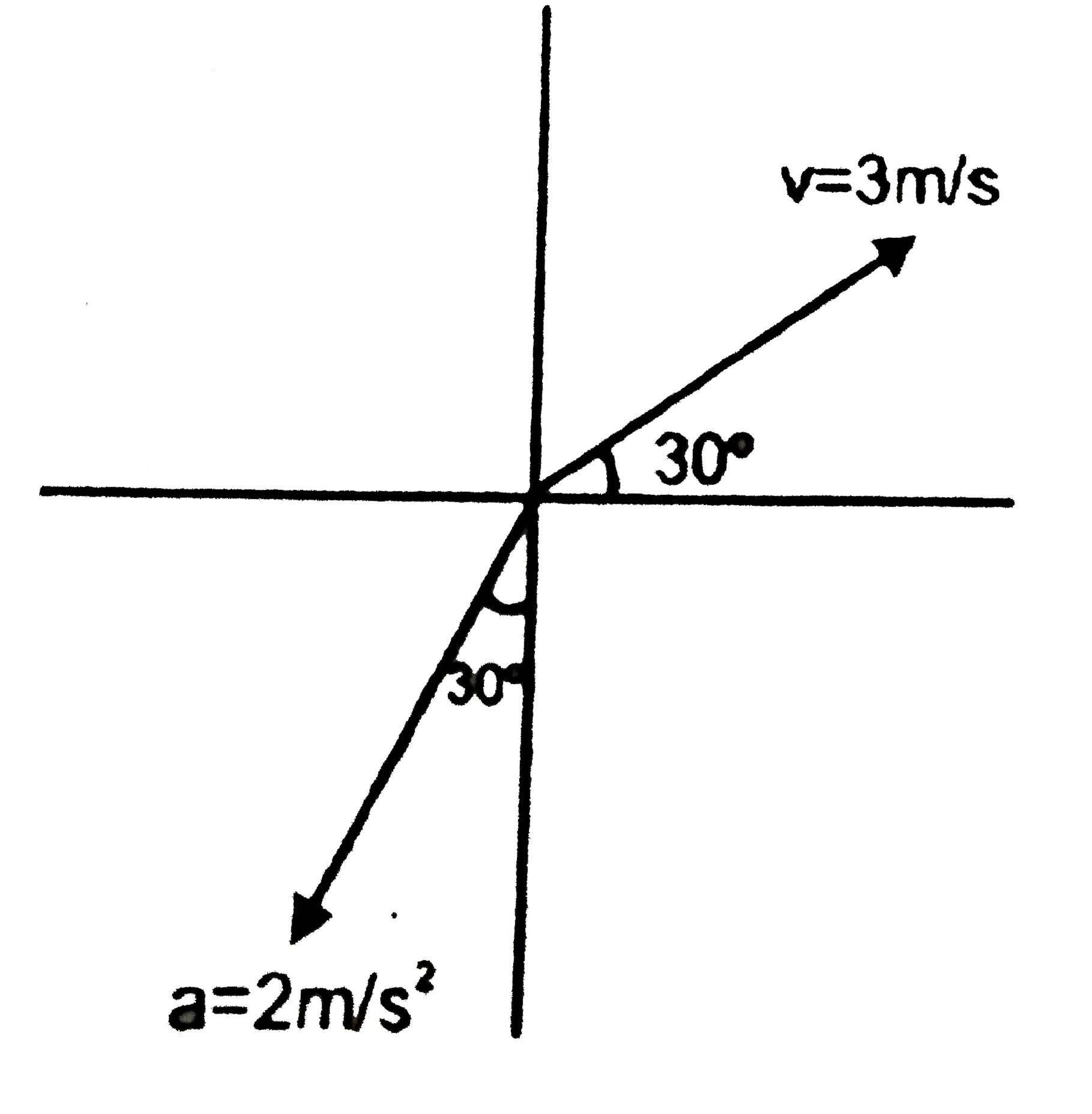
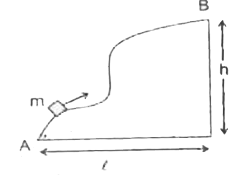
View SolutionA particle of mass m is pulled along an arbitrary curved surface without acceleration as shown in figure. Coefficient of friction between surface and particle is μ. Then

codes:
View SolutionA particle is given an intial speed u inside a smooth spherical shell of radius R so that it is just able to complete the circle. Acceleration of the particle, when its velocity is vertical, is

View SolutionA spherical hole of radius R/2 is excavated from the asteroid of mass M as shown in the figure the gravitational acceleration at a point on the surface of the asteroid just above the excavation is

View SolutionA solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if

r<x<2r
View SolutionA solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if

x>2R
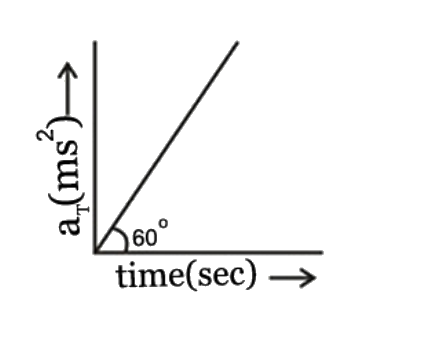
View SolutionTangental acceleration of a particle moving in a circle of radius 1 m varies with time t as shown in figure (initial velocity of the particle is zero). Time after which total acceleration of particle makes an angle of 30∘ with radial acceleration is
View Solution
