Points P,Q and R are in vertical line such that PQ=QR. A ball at (P) is allowed to fall freely. What is the ratio of the times of descent through PQ and QR ?
0.042361111111111
1 : √2
1:(√2 - 1)
1 : (√2 + 1)
The correct Answer is:(c )
To solve the problem, we need to find the ratio of the times of descent through the segments PQ and QR, given that the distances PQ and QR are equal. Let's denote the distance PQ = QR = H.
1. Define the Variables:
- Let the distance between points P and Q be H.
- Let the distance between points Q and R also be H.
- Let t1 be the time taken to fall from P to Q.
- Let t2 be the time taken to fall from Q to R.
2. Use the Equation of Motion for PQ:
- Since the ball is dropped from rest, the initial velocity u=0.
- The equation of motion for the distance H can be written as:
H=ut1+12gt21
- Substituting u=0:
H=12gt21
3. Use the Equation of Motion for PR:
- The total distance from P to R is 2H.
- The time taken to fall from P to R is t1+t2.
- The equation of motion for the distance 2H can be written as:
2H=u(t1+t2)+12g(t1+t2)2
- Again substituting u=0:
2H=12g(t1+t2)2
4. Relate the Two Equations:
- From the first equation, we can express H:
H=12gt21⟹2H=gt21
- Substitute 2H in the second equation:
gt21=12g(t1+t2)2
- Dividing both sides by g (assuming g≠0):
t21=12(t1+t2)2
5. Simplify the Equation:
- Multiply both sides by 2:
2t21=(t1+t2)2
- Expanding the right side:
2t21=t21+2t1t2+t22
- Rearranging gives:
t21−2t1t2−t22=0
6. Solve the Quadratic Equation:
- This is a quadratic equation in terms of t1:
t21−2t1t2−t22=0
- Using the quadratic formula t1=−b±√b2−4ac2a:
- Here, a=1,b=−2t2,c=−t22:
t1=2t2±√(2t2)2−4(−t22)2
t1=t2±t2√2
7. Find the Ratio t1t2:
- We can express t1 in terms of t2:
t1=t2(√2−1)
- Thus, the ratio t1t2 is:
t1t2=√2−1
Final Answer:
The ratio of the times of descent through PQ and QR is:
t1t2=√2−1
- Let the distance between points P and Q be H.
- Let the distance between points Q and R also be H.
- Let t1 be the time taken to fall from P to Q.
- Let t2 be the time taken to fall from Q to R.
- Since the ball is dropped from rest, the initial velocity u=0.
- The equation of motion for the distance H can be written as:
H=ut1+12gt21
- Substituting u=0:
H=12gt21
- The total distance from P to R is 2H.
- The time taken to fall from P to R is t1+t2.
- The equation of motion for the distance 2H can be written as:
2H=u(t1+t2)+12g(t1+t2)2
- Again substituting u=0:
2H=12g(t1+t2)2
- From the first equation, we can express H:
H=12gt21⟹2H=gt21
- Substitute 2H in the second equation:
gt21=12g(t1+t2)2
- Dividing both sides by g (assuming g≠0):
t21=12(t1+t2)2
- Multiply both sides by 2:
2t21=(t1+t2)2
- Expanding the right side:
2t21=t21+2t1t2+t22
- Rearranging gives:
t21−2t1t2−t22=0
- This is a quadratic equation in terms of t1:
t21−2t1t2−t22=0
- Using the quadratic formula t1=−b±√b2−4ac2a:
- Here, a=1,b=−2t2,c=−t22:
t1=2t2±√(2t2)2−4(−t22)2
t1=t2±t2√2
- We can express t1 in terms of t2:
t1=t2(√2−1)
- Thus, the ratio t1t2 is:
t1t2=√2−1
The ratio of the times of descent through PQ and QR is:
t1t2=√2−1
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBook:NCERT FINGERTPS ENGLISHChapter:MOTION IN A STRAIGHT LINEExercise:NCERT EXEMPLAR PROBLEMS
Explore 6 Videos
- MOTION IN A STRAIGHT LINEBook:NCERT FINGERTPS ENGLISHChapter:MOTION IN A STRAIGHT LINEExercise:ASSERTION AND REASON
Explore 15 Videos
- MOTION IN A STRAIGHT LINEBook:NCERT FINGERTPS ENGLISHChapter:MOTION IN A STRAIGHT LINEExercise:RELATIVE VELOCITY
Explore 18 Videos
- MOTION IN A PLANE Book:NCERT FINGERTPS ENGLISHChapter:MOTION IN A PLANE Exercise:Assertion And Reason
Explore 15 Videos
- OSCILLATIONS Book:NCERT FINGERTPS ENGLISHChapter:OSCILLATIONS Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
PQ is a smooth inclined plane whose angle θ can be varied in such a way that point Q remains fixed and P can move on a vertical line PR. A particle slides from rest from point P at different value of θ time for descent from P and Q is noted. The following statement (s) is / are correct about the time of descent :

A. the minimum time of descent is 2√l/g
B. the time descent is minimum continuously as θ is increased
C. the time of descent decreases continuously as θ is increased
D. the time of descent first decreases then increases.
View SolutionA ball falls freely from rest. The ratio of the distance travelled in first, second, third and fourth second is
View Solution
Knowledge Check
Points A and B are on the number line in such a way that A corresponds to 0.625 and B corresponds to 0.637 . If P is the midpoint of ¯¯¯¯¯¯AB , and Q is on the number line two-thirds of the distance from A to B , what is the ratio of PQ to AQ ?
A1:4B1:3C1:2D2:3
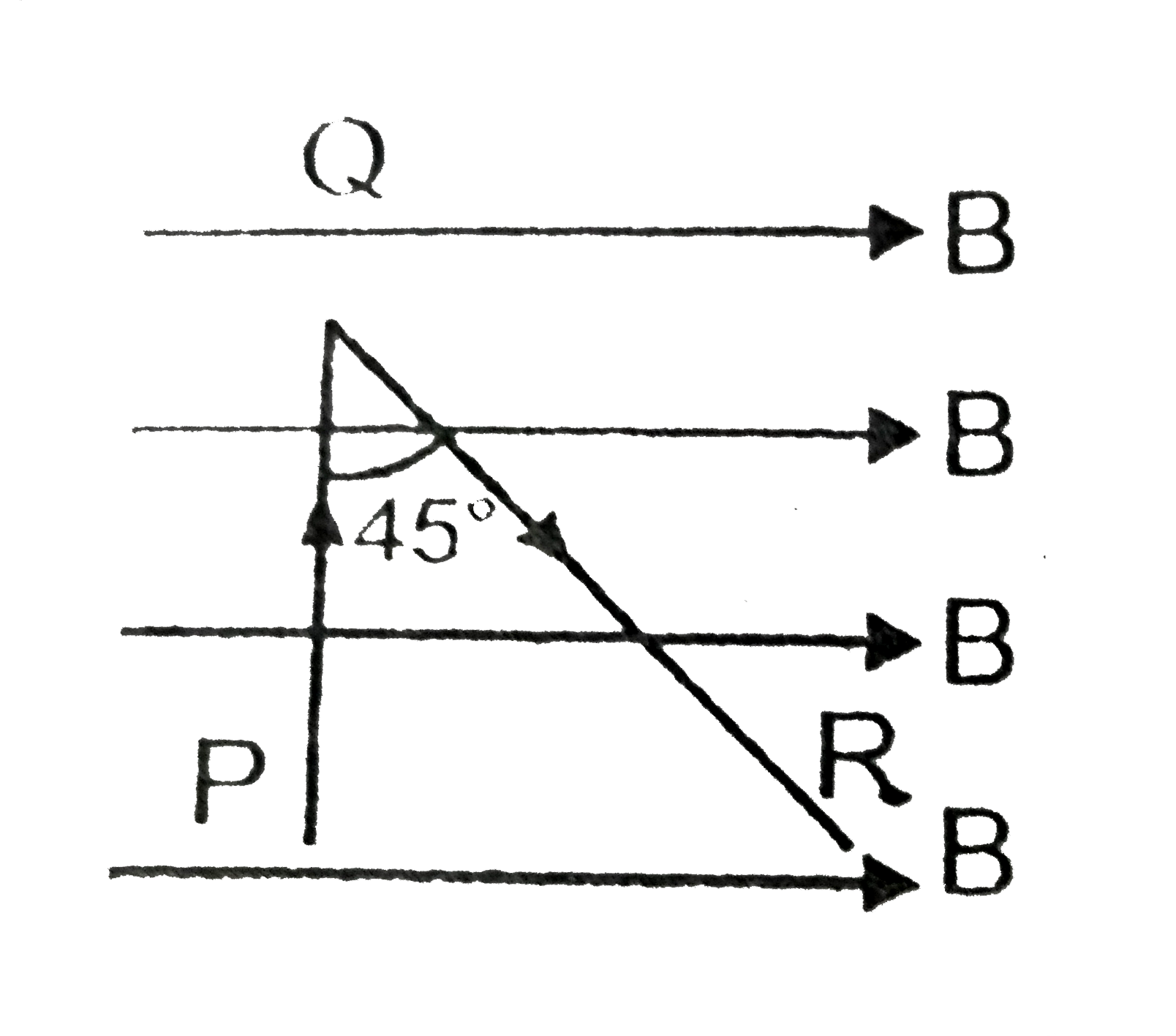
A wire PQR carrying a current l is bent as shown in the figure. It is placed in a uniform magnetic field B. What is the ratio of magnitude of the force on PQ to that on QR ?
View SolutionThe perpendicular from P and QR in the triangle jPQR meets QR at S. Alsl, T is a point on SR sch that QS =3cm,ST=4cm,andT=8cm. Find the ratio of the areas of the triangles PQS , PST and PTR.
View SolutionPoints P (a, -4), Q (-2, b) and R (0, 2) are collinear. If lies between P and R, such that PR = 2QR, calculate the values of a and b.
View SolutionA line intersects the y-axis and x-axis at the points P and Q respectively. If (2, 5) is the mid-point of PQ, then find the coordinates of P and Q.
View SolutionA river of width ω is flowing with a uniform velocity v. A boat starts moving from point P also With velocity v relative to the river. The direction of resultant velocity is always perpendicular to the line joining boat and the fixed point R. Point Q is on the opposite side of the river. P, Q and R are in a straight line. If PQ=QR=ω, find (a) the trajectory of the boat, (b) the drifting of the boat and (c) the time taken by the boat to cross the river.
View Solution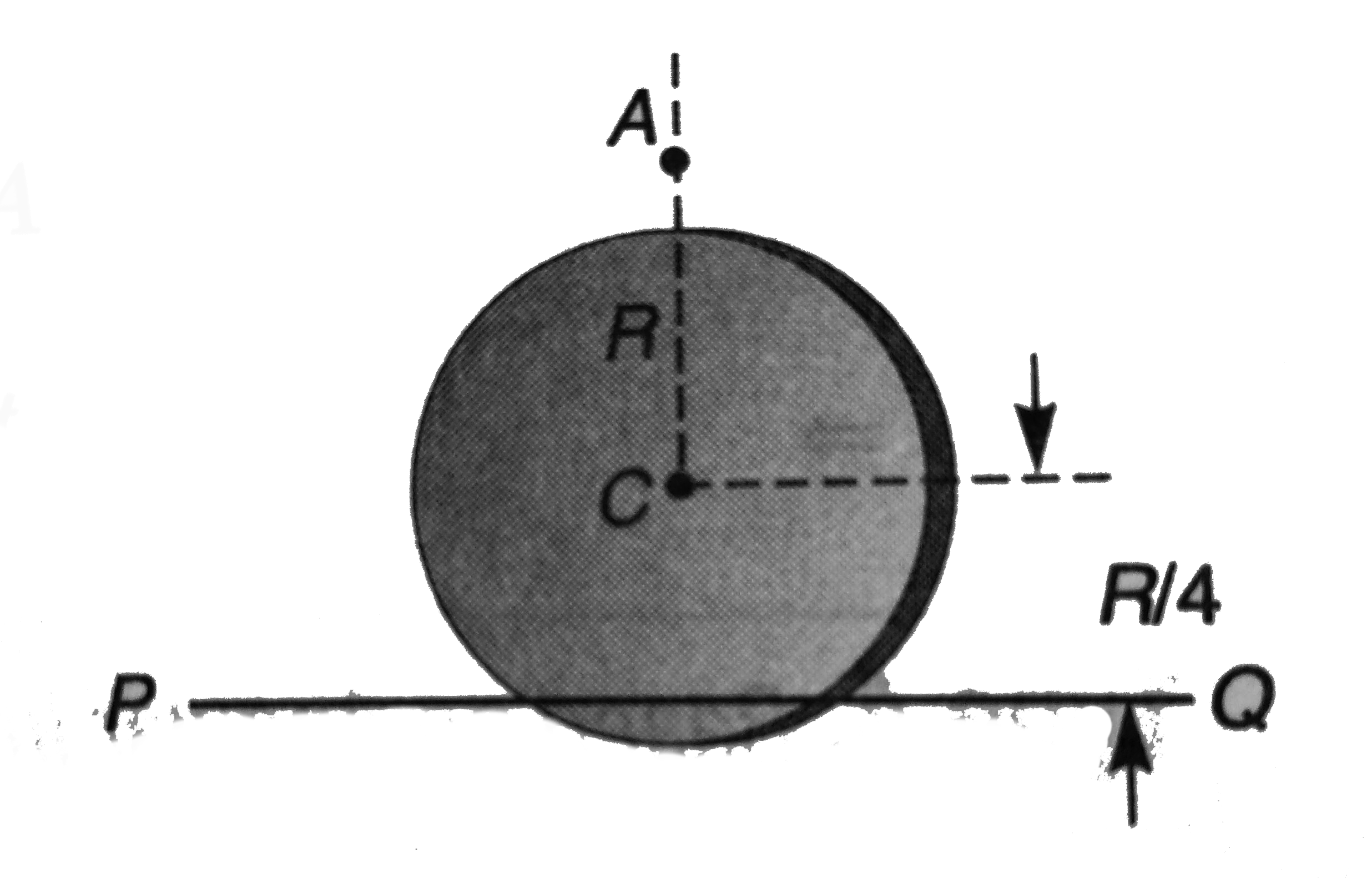
A uniform circular disc has radius R and mass m. A particle, also of mass m, if fixed at a point A on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially the disc is held vertical with the point A at its highest position. it is then allowed to fall, so that it starts rotation about PQ. Find the linear speed of the particle as it reaches its lowest position.
View SolutionConstruct a triangle PQR such that PQ = QR = 4 . 7 cm and ∠Q=72∘ . Measure angles P and R . Name the triangle
View Solution