A particle of mass m moves on the x−aξs as follows : it starts from rest at t=0, from the point x=0, and comes to rest at t=l at the point x=1. No other information is available about its motion at intermediate times (0<t<l) . If α denotes the instantaneous accelartion of the particle , then :
α cannot remain positive for all t in the interval 0≤t≤1.
|α| cannot exceed 2 at any point in its path .
|α| must be ≥4 at some point or points in its path .
α must change sign during the motion , but no other assertion can be made with the information given .
The correct Answer is:A, C, D
Note : α cannot remain positive for all t in the interval 0≤t≤1. This is because since the body starts from rest , it will first accelerate . Finally it stops therfore α will become negative . Therfore α will change its direction. options (a) and (d) are correct .
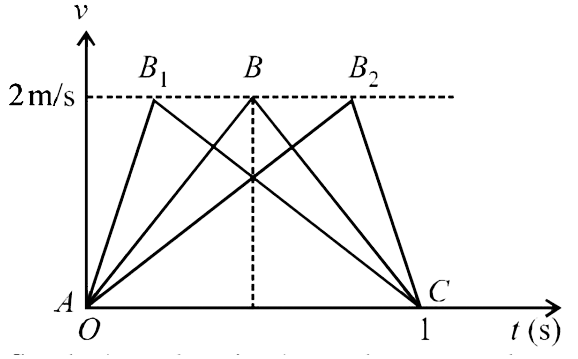
Let the particle accelerate uniformly till half the distance (A→B) and then retard uniformly in the remaining half distance (B→C) .
The total time is 1sec. Therfore the time taken from A→Bis0.5sec.
For A→B
S=ut+12at20.5=0+12×a×(0.5)2 ltbr gt ∴a=4m/s2
∴VB=0+4×0.5=2m/s2
Note : Now , if the particle accelerates till B2 then for covering the same total distance in same time , acceleration should be less than 4m/s2 but |dee≤ration| till B1 , then for covering the same total distance in the same time , the acceleration should be greater than 4m/s2 and |dece≤ration|<4m/s2. The same is dipcted by the graph .
So, the |ae≤ration| must be greater than or equal to 4m/s2 at some point or points in the path .
Topper's Solved these Questions
Similar Questions
A particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5s ?
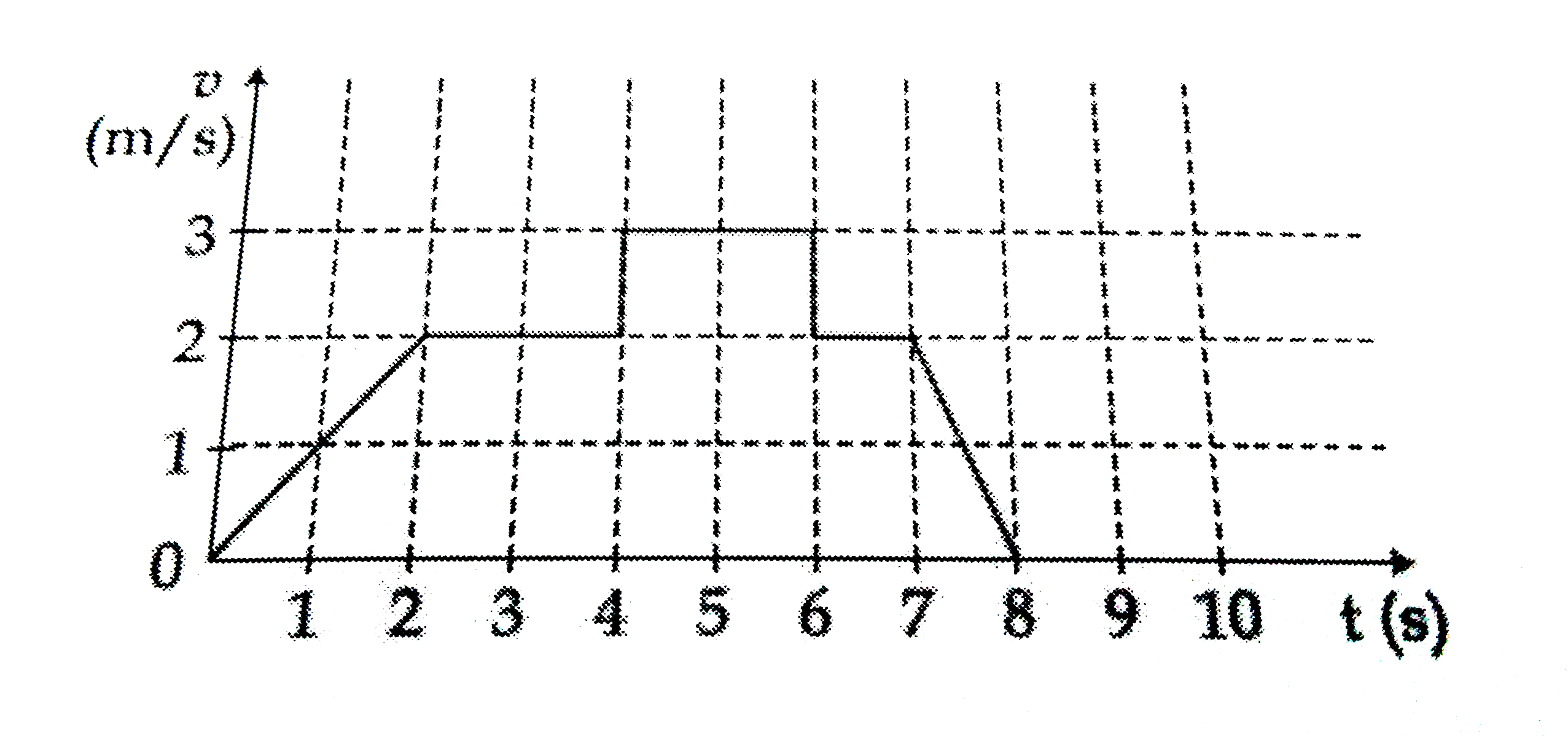
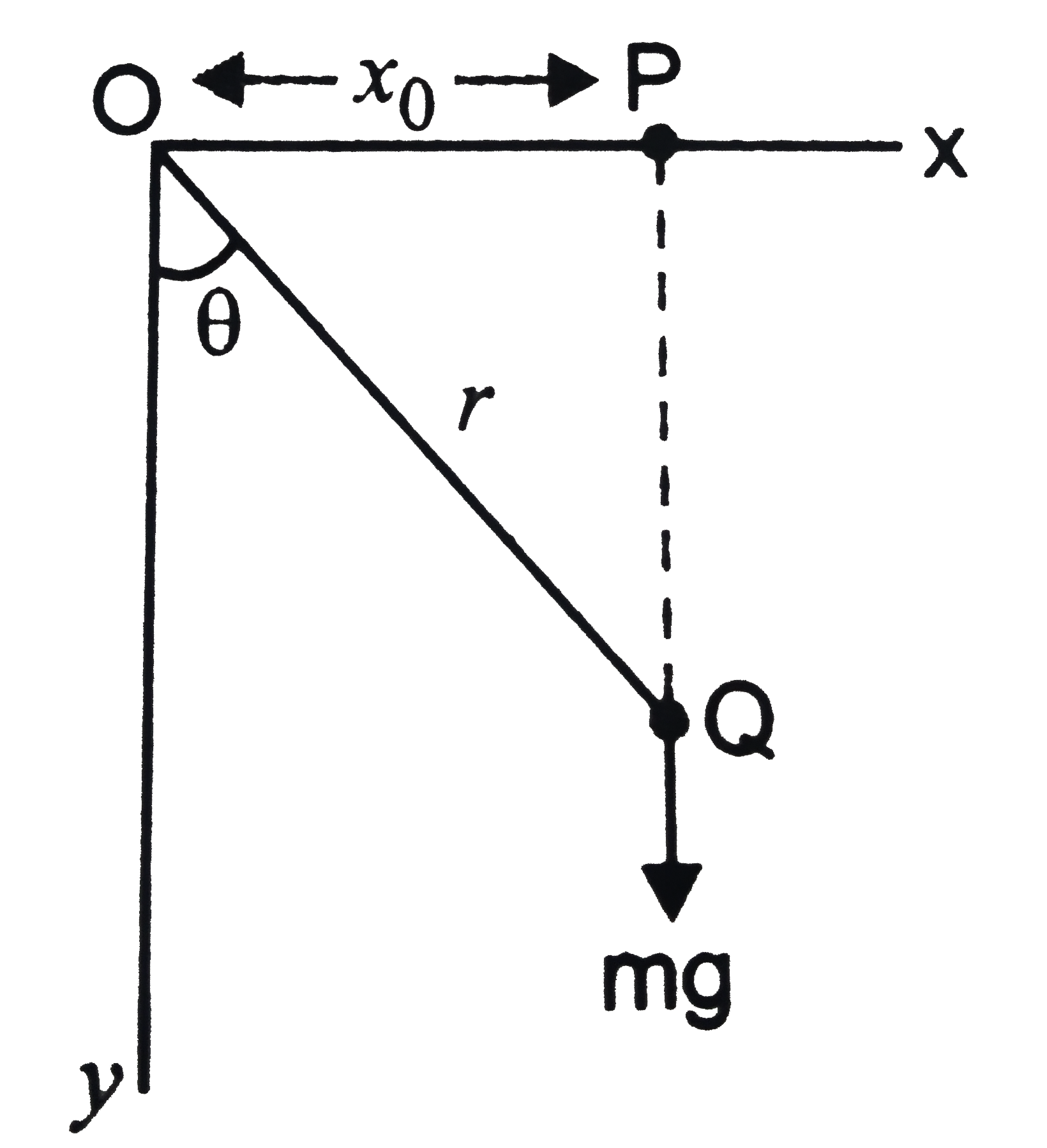
View SolutionA particle of mass m is released from rest from point P at x=x0 on X-axis from origin O and falls vertically along y-axis as shown in Fig. What is the magnitude of the torque acting on the particle at time t, when it is at the point Qw.r.t.O ?
View Solution
Knowledge Check
A particle of mass m moves on the x-axis as follows: It starts from rest at r= 0 from the pointr=0, and come to rest at 1 at the point x = 1. The velocity changes lincarly with time. No other information is available about its motion at intermediate times [0<t<1] . If α denotes the instantaneous acceleration of the particle , then
Aα cannot remain positive for all t in the interval 0 to 1B|α| cannot exceed 2 at any point in its pathC|α| must be > 4 some point or points in its pathDαmust change sign during the motion, but no other assertion can be made with the given information.A point moving along the x- direction starts from rest at x=0 and comes to rest at x=1 after 1 s. Its acceleration at any point is denoted by α . Which of the following is not correct ?
Aα must change sign during the motion.B|α|≥4 units at some or all points during the motion.CIt is not possible to specify an upper limit for |α| from the given data.D|α| cannot be less than 1/2 during the motion.A point moving along the x-direction starts from rest at x=0 and comes to rest at x=1 after 1 s Its accelertion at any point is denoted by α Which of following is not correct ?
Aα must change sign during the motion .B|α|ge 4 units st some or all points during the motion.CIt is not possible to specify an uppwer limit for |α| from the given data.D|α| connot be less that 1/2 during the motion.
At t=0 aparticle of mass m start moving from rest due to a force →F=F0sin(ωt)ˆi :
View SolutionA particle is moving under constant acceleration a=kt. The motion starts from rest. The velocity and displacement as a function of time t is
View SolutionA particle is moving along the x-axis whose acceleration is given by a=3x−4, where x is the location of the particle. At t = 0, the particle is at rest at x=4/3m. The distance travelled by the particles in 5 s is
View SolutionA particle of mass m is moving in a straight line is acted on by an attractive force mk2a2x2 for x≥aand2mK2xa for x<2.If the particle starts from rest at the point x = 2a, then it will reach the point x = 0 with a speed
View SolutionA particle starts from rest with a time varying acceleration a=(2t−4). Here t is in second and a in m/s2
Particle comes to rest after a time t=………… second
View Solution
