A particle of mass m moving in the x direction with speed 2v is hit by another particle of mass 2m moving in they y direction with speed v. If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to :
56%
62%
44%
50%
The correct Answer is:A
To solve the problem of the perfectly inelastic collision between two particles, we will follow these steps:
Step 1: Determine Initial Momentum
We have two particles:
- Particle 1: mass m, moving in the x-direction with speed 2v.
- Particle 2: mass 2m, moving in the y-direction with speed v.
The initial momentum in the x-direction (Pinitial,x) is:
Pinitial,x=m⋅2v=2mv
The initial momentum in the y-direction (Pinitial,y) is:
Pinitial,y=2m⋅v=2mv
Step 2: Apply Conservation of Momentum
Since the collision is perfectly inelastic, the two particles will stick together after the collision. Let Vx and Vy be the final velocities in the x and y directions, respectively.
Using conservation of momentum in the x-direction:
Pinitial,x=Pfinal,x
2mv=(3m)Vx(total mass after collision is 3m)
Vx=2mv3m=23v
Using conservation of momentum in the y-direction:
Pinitial,y=Pfinal,y
2mv=(3m)Vy
Vy=2mv3m=23v
Step 3: Calculate Initial Kinetic Energy
The initial kinetic energy (KEinitial) is the sum of the kinetic energies of both particles:
KEinitial=12m(2v)2+12(2m)v2
=12m⋅4v2+12⋅2m⋅v2
=2mv2+mv2=3mv2
Step 4: Calculate Final Kinetic Energy
The final kinetic energy (KEfinal) after the collision is:
KEfinal=12(3m)(V2x+V2y)
Substituting Vx and Vy:
=12(3m)((23v)2+(23v)2)
=12(3m)(49v2+49v2)
=12(3m)(89v2)
=12mv218=2mv23
Step 5: Calculate Percentage Loss in Kinetic Energy
The percentage loss in kinetic energy is given by:
Percentage Loss=KEinitial−KEfinalKEinitial×100
=3mv2−2mv233mv2×100
=9mv2−2mv29mv2×100
=7mv29mv2×100=7009≈77.78%
Thus, the percentage loss in energy during the collision is approximately 77.78%.
We have two particles:
- Particle 1: mass m, moving in the x-direction with speed 2v.
- Particle 2: mass 2m, moving in the y-direction with speed v.
Pinitial,x=m⋅2v=2mv
Pinitial,y=2m⋅v=2mv
Since the collision is perfectly inelastic, the two particles will stick together after the collision. Let Vx and Vy be the final velocities in the x and y directions, respectively.
Pinitial,x=Pfinal,x
2mv=(3m)Vx(total mass after collision is 3m)
Vx=2mv3m=23v
Pinitial,y=Pfinal,y
2mv=(3m)Vy
Vy=2mv3m=23v
The initial kinetic energy (KEinitial) is the sum of the kinetic energies of both particles:
KEinitial=12m(2v)2+12(2m)v2
=12m⋅4v2+12⋅2m⋅v2
=2mv2+mv2=3mv2
The final kinetic energy (KEfinal) after the collision is:
KEfinal=12(3m)(V2x+V2y)
Substituting Vx and Vy:
=12(3m)((23v)2+(23v)2)
=12(3m)(49v2+49v2)
=12(3m)(89v2)
=12mv218=2mv23
The percentage loss in kinetic energy is given by:
Percentage Loss=KEinitial−KEfinalKEinitial×100
=3mv2−2mv233mv2×100
=9mv2−2mv29mv2×100
=7mv29mv2×100=7009≈77.78%
Topper's Solved these Questions
Similar Questions
A particle of mass m moving with velocity 2v collides with another particle of mass 3m moving with velocity v in the same direction.If it is perfect inelastic collision,the loss of kinetic energy of the system is
View SolutionA particle of mass m moving on a smooth surface with velocity 10m/s strikes another particle of mass 2m moving with 5m/s in the same direction . If the collision is elastic and head - on , find velocities of particles after the collision.
View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass m moving in the x direction with speed 2v is hit by another particle of mass 2m moving in they y direction with speed v. If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to :
A56%B62%C44%D50% - Question 2 - Select One
A particle of mass m moving in the x direction with speed 2v is hit by another particle of mass 2m moving in they y direction with speed v. If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to :
Adevelopement of air current when the plate is placedBinduction of electrical charge on the plateCshielding of magnetic lines of force as aluminium is a paramagnetic material.Delectromagnetic induction in the aluminium plate giving rise to electromagnetic damping. - Question 3 - Select One
A particle of mass m moving in the x direction with speed 2v is hit by particle of mass 2m moving in the y direction with speed v. If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to:
A0.44B0.5C0.56D0.62
A particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionTwo particles of mass 2m and m moving with speed v and 2v respectively pependicular to each other collides perfectly inelastically, then

Speed of the particles after collisionView SolutionTwo particles of mass 2m and m moving with speed v and 2v respectively perpendicular to each other collides perfectly inelastically, then
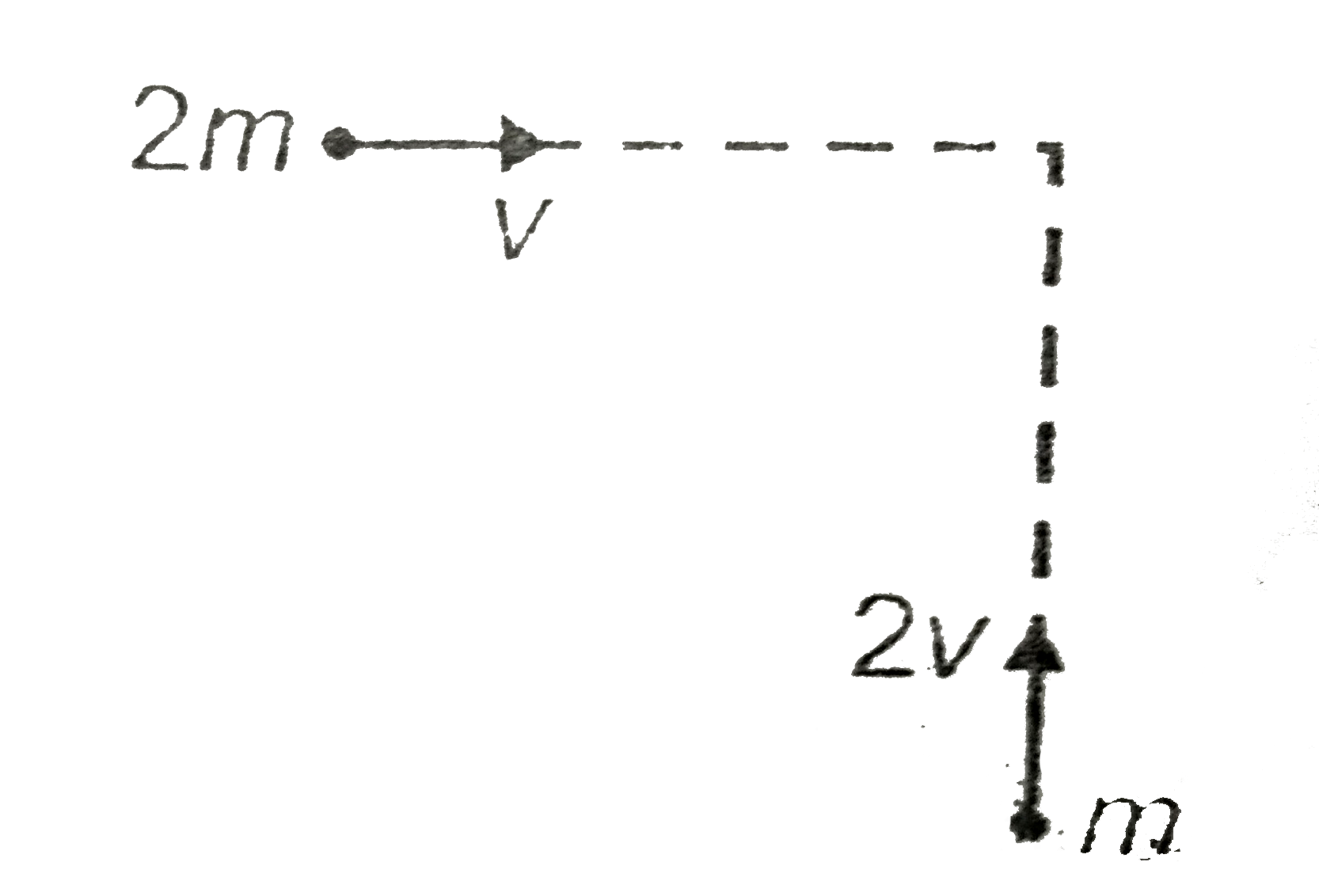
Loss in kinetic energy of the systemView SolutionTwo ball bearings of mass m each moving in opposite directions with same speed v collide head on with each other. If the collision is perfectly elastic, what will be the outcome of the collision ?
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 3 m at rest. Loss of KE of system in the collision is
View Solution

