Question

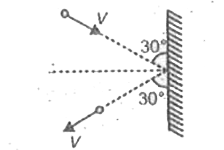
A particle of mass M strikes a wall at an angle of incidence ${60}^{\circ }$ with velocity V elastically Then the change in momentum is

Options

A. `(MV)/2`
B. `MV`
C. `-2MV`
D. zero

Answer

B

Explanation

To find the change in momentum of a particle of mass $$M$$ striking a wall at an angle of incidence $${60}^{\circ }$$ with velocity $$V$$ elastically, we can follow these steps:

Step 1: Understand the scenario
The particle strikes the wall at an angle of \( 60^\circ \). In an elastic collision, the angle of incidence is equal to the angle of reflection. Therefore, the particle will leave the wall at the same angle \( 60^\circ \) after the collision.

Step 2: Resolve the velocity into components
The initial velocity \( V \) can be resolved into two components:
- The horizontal (x-axis) component:
\( V_x = V \cos(60^\circ) = V \cdot \frac{1}{2} = \frac{V}{2} \)
- The vertical (y-axis) component:
\( V_y = V \sin(60^\circ) = V \cdot \frac{\sqrt{3}}{2} \)

Step 3: Calculate initial momentum
Before the collision, the momentum in the x-direction and y-direction can be calculated as follows:
- Initial momentum in the x-direction:
\( P_{ix} = M V_x = M \cdot \frac{V}{2} = \frac{MV}{2} \)
- Initial momentum in the y-direction:
\( P_{iy} = M V_y = M \cdot V \cdot \frac{\sqrt{3}}{2} = \frac{MV\sqrt{3}}{2} \)

Step 4: Calculate final momentum after collision
After the collision, the x-component of the velocity will be in the opposite direction, while the y-component remains the same:
- Final momentum in the x-direction:
\( P_{fx} = M (-V_x) = M \left(-\frac{V}{2}\right) = -\frac{MV}{2} \)
- Final momentum in the y-direction:
\( P_{fy} = M V_y = M \cdot V \cdot \frac{\sqrt{3}}{2} = \frac{MV\sqrt{3}}{2} \)

Step 5: Calculate change in momentum
Now we can calculate the change in momentum for both x and y directions:
- Change in momentum in the x-direction:
\( \Delta P_x = P_{fx} - P_{ix} = -\frac{MV}{2} - \frac{MV}{2} = -MV \)
- Change in momentum in the y-direction:
\( \Delta P_y = P_{fy} - P_{iy} = \frac{MV\sqrt{3}}{2} - \frac{MV\sqrt{3}}{2} = 0 \)

Step 6: Final result
The total change in momentum is primarily in the x-direction because the y-direction momentum remains unchanged. Therefore, the change in momentum is:
\( \Delta P = \Delta P_x = -MV \)

Summary
The change in momentum of the particle after striking the wall is \( -MV \) in the x-direction, and there is no change in the y-direction.

---