A photon of wavelength 0.1A is emitted by a helium atom as a consequence of the emission of photon. The KE gained by helium atom is
0.05eV
1.05 eV
2.05 eV
3.05 eV
The correct Answer is:C
To solve the problem of finding the kinetic energy gained by a helium atom when a photon of wavelength 0.1Å is emitted, we can follow these steps:
1. Understand the relationship between energy and momentum:
The kinetic energy (KE) gained by the helium atom can be expressed in terms of momentum p:
KE=p22m
where m is the mass of the helium atom.
2. Relate momentum to wavelength:
The momentum p of a photon can be expressed using the Planck's constant h and the wavelength λ:
p=hλ
3. Substitute momentum into the kinetic energy formula:
Substitute the expression for momentum into the kinetic energy formula:
KE=(h/λ)22m=h22mλ2
4. Insert known values:
- Planck's constant h=6.63×10−34Js
- Mass of helium atom m=4×1.67×10−27kg=6.68×10−27kg
- Wavelength λ=0.1Å=0.1×10−10m=1×10−11m
5. Calculate the kinetic energy:
Substitute the values into the kinetic energy formula:
KE=(6.63×10−34)22×(6.68×10−27)×(1×10−11)2
Calculating the numerator:
(6.63×10−34)2=4.39×10−67
Calculating the denominator:
2×(6.68×10−27)×(1×10−11)2=2×6.68×10−27×1×10−22=1.336×10−48
Now, substituting these into the equation:
KE=4.39×10−671.336×10−48≈3.29×10−19J
6. Convert the energy to electron volts:
To convert joules to electron volts, use the conversion factor 1eV=1.6×10−19J:
KE≈3.29×10−191.6×10−19≈2.06eV
Final Answer:
The kinetic energy gained by the helium atom is approximately 2.06eV.
---
The kinetic energy (KE) gained by the helium atom can be expressed in terms of momentum p:
KE=p22m
where m is the mass of the helium atom.
The momentum p of a photon can be expressed using the Planck's constant h and the wavelength λ:
p=hλ
Substitute the expression for momentum into the kinetic energy formula:
KE=(h/λ)22m=h22mλ2
- Planck's constant h=6.63×10−34Js
- Mass of helium atom m=4×1.67×10−27kg=6.68×10−27kg
- Wavelength λ=0.1Å=0.1×10−10m=1×10−11m
Substitute the values into the kinetic energy formula:
KE=(6.63×10−34)22×(6.68×10−27)×(1×10−11)2
(6.63×10−34)2=4.39×10−67
2×(6.68×10−27)×(1×10−11)2=2×6.68×10−27×1×10−22=1.336×10−48
KE=4.39×10−671.336×10−48≈3.29×10−19J
To convert joules to electron volts, use the conversion factor 1eV=1.6×10−19J:
KE≈3.29×10−191.6×10−19≈2.06eV
The kinetic energy gained by the helium atom is approximately 2.06eV.
Topper's Solved these Questions
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Multiple Correct
10 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Linked Comprehension
44 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Subjective
16 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.5
14 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
Similar Questions
The two electrons in helium atom
View SolutionA monochromatic source emitting light of wavelength 600 nm has a power output of 66 W. Calculate the number of photons emitted by this source in 2 minutes.
View SolutionA helium atom on losing an electron becomes
View SolutionThe sum of all the quantum number of helium atom is
View SolutionA near ultra violet photon of wavelength 300nm is absorbed by a gas and then emitted as two photons. One photons is of red light with wavelength 760nm. What would be the wave length of the second photon?
View SolutionAn atom absorbs a photon of wavelength 500nm and emits another photon of wavelength 700nm. Find the net energy absorbed by the atom in the process.
View SolutionMonochromatic light of wavelength 667nm is produced by a helium neon laser . The power emitted is 9mW . The number of photons arriving per second on the average at a target irradiated by this beam is
View SolutionThe following diagram indicates the energy levels of a certain atom when the system moves from 4E level to E. A photon of wavelength λ1 is emitted. The wavelength of photon produced during its transition from 73E level to E is λ2. the ratio λ1λ2 will be
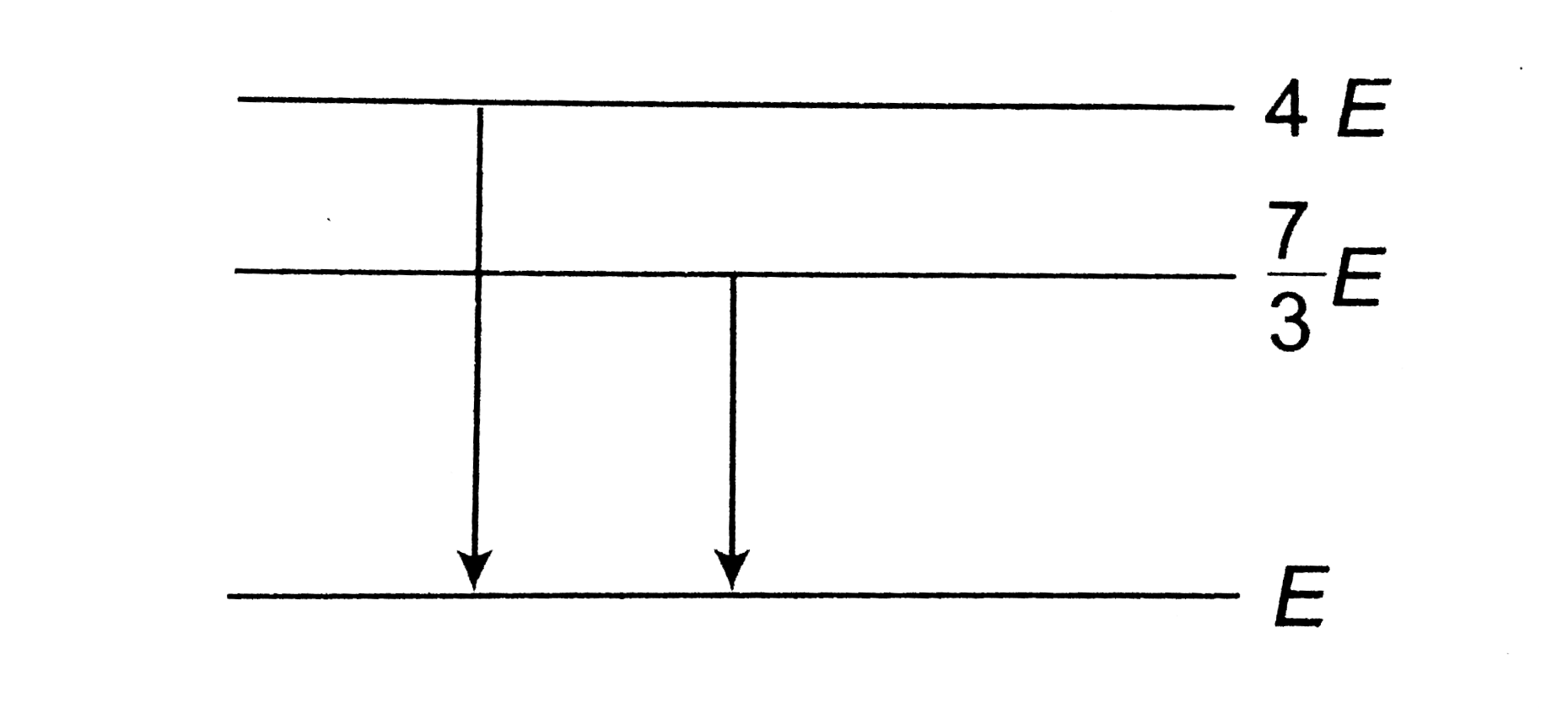
View SolutionThe following diagram indicates the energy levels of a certain atom when the system moves from 4E level to E. A photon of wavelength λ1 is emitted. The wavelength of photon produced during its transition from 73E level to E is λ2. the ratio λ1λ2 will be

View SolutionA photon of energy 10.2 eV corresponds to light of wavelength λ0. Due to an electron transition from n=2 to n=1 in a hydrogen atom, light of wavelength λ is emitted. If we take into account the recoil of the atom when the photon is emitted.
View Solution
