A piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
agk
a2gk
2agk
a4gk
The correct Answer is:B
To solve the problem, we will analyze the forces acting on the bead when the wire is accelerated. The bead will find a new equilibrium position due to the acceleration of the wire.
1. Understand the System:
The wire is bent in the shape of a parabola described by the equation y=kx2. The bead is initially at the lowest point of the parabola when the wire is at rest.
2. Identify Forces Acting on the Bead:
When the wire is accelerated with a constant acceleration a parallel to the x-axis, the bead experiences two main forces:
- The gravitational force acting downwards, →Fg=mg.
- A pseudo force acting on the bead due to the acceleration of the wire, →Fp=ma, acting in the opposite direction of the acceleration.
3. Set Up the Coordinate System:
Let θ be the angle that the tangent to the parabola makes with the horizontal at the position of the bead. The forces can be resolved into components along the tangent and normal directions.
4. Resolve Forces:
- The component of the weight acting along the tangent to the parabola is mgsin(θ).
- The component of the pseudo force acting along the tangent is macos(θ).
5. Apply Equilibrium Condition:
For the bead to be in equilibrium, the net force along the tangent must be zero:
mgsin(θ)=macos(θ)
Rearranging gives:
tan(θ)=ag
6. Relate tan(θ) to the Parabola:
The slope of the parabola at any point is given by the derivative:
tan(θ)=dydx=d(kx2)dx=2kx
Therefore, we have:
2kx=ag
7. Solve for x:
Rearranging the equation gives:
x=a2gk
8. Conclusion:
The distance of the new equilibrium position of the bead from the y-axis is:
x=a2gk
Final Answer:
The distance of the new equilibrium position of the bead from the y-axis is a2gk.
The wire is bent in the shape of a parabola described by the equation y=kx2. The bead is initially at the lowest point of the parabola when the wire is at rest.
When the wire is accelerated with a constant acceleration a parallel to the x-axis, the bead experiences two main forces:
- The gravitational force acting downwards, →Fg=mg.
- A pseudo force acting on the bead due to the acceleration of the wire, →Fp=ma, acting in the opposite direction of the acceleration.
Let θ be the angle that the tangent to the parabola makes with the horizontal at the position of the bead. The forces can be resolved into components along the tangent and normal directions.
- The component of the weight acting along the tangent to the parabola is mgsin(θ).
- The component of the pseudo force acting along the tangent is macos(θ).
For the bead to be in equilibrium, the net force along the tangent must be zero:
mgsin(θ)=macos(θ)
Rearranging gives:
tan(θ)=ag
The slope of the parabola at any point is given by the derivative:
tan(θ)=dydx=d(kx2)dx=2kx
Therefore, we have:
2kx=ag
Rearranging the equation gives:
x=a2gk
The distance of the new equilibrium position of the bead from the y-axis is:
x=a2gk
The distance of the new equilibrium position of the bead from the y-axis is a2gk.
Topper's Solved these Questions
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - More than one choice is correct
15 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Assertion- Reason
4 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Problem for practice
30 Videos
- BASIC MATHEMATICSBOOK - GRB PUBLICATIONCHAPTER - BASIC MATHEMATICSEXERCISE - Problems For Practice
35 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type
11 Videos
Similar Questions
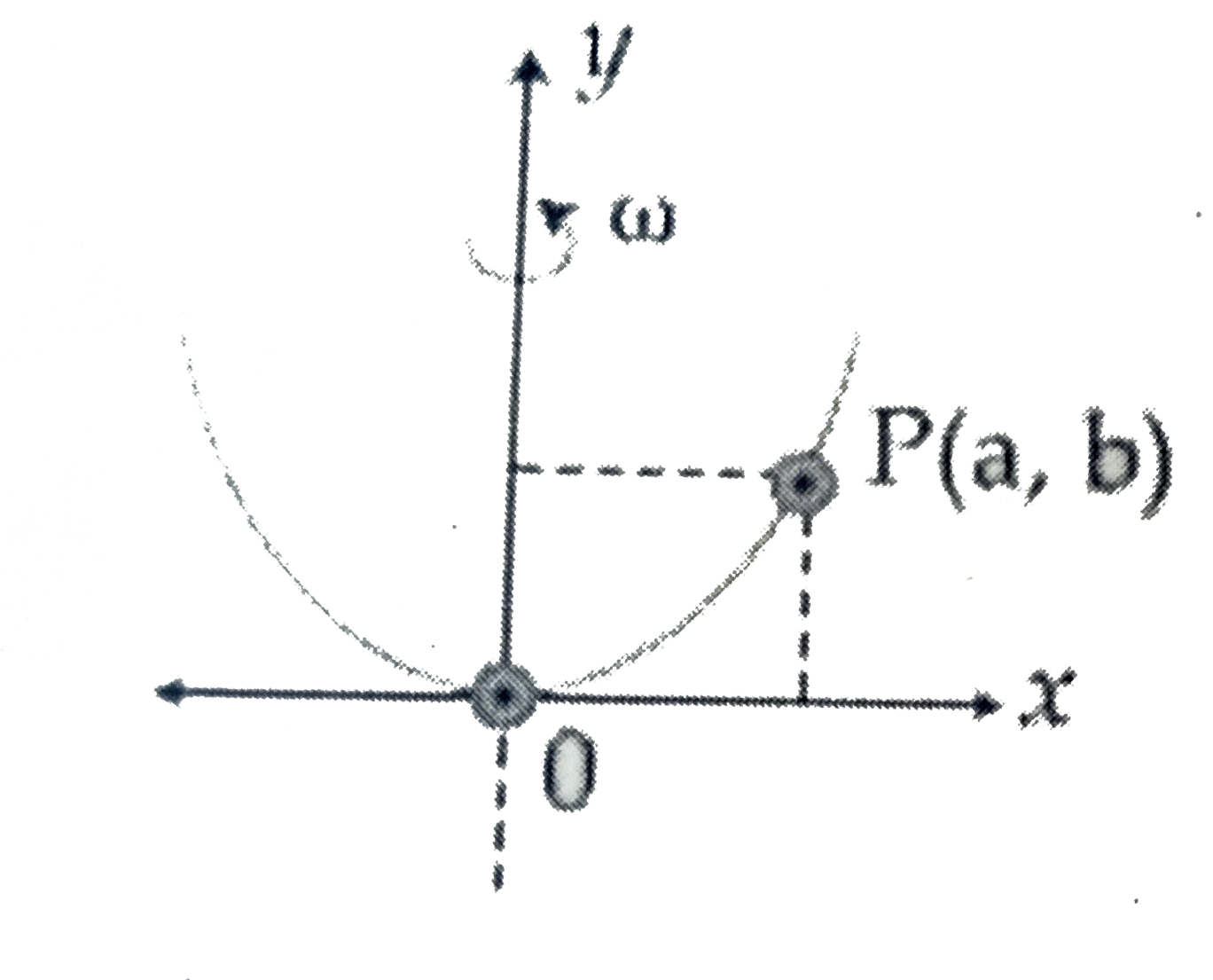
A bead of mass m stays at point P (a,b) on a wire bent in the shape of a parabola y=4Cx2 and rotating with angular speed ω (see figure ) . The value of ω is (neglect friction),
View SolutionA wire when bent in a shape of equilateral triangle encloses area of 726 sq units. Find the area when the wire is bent in the shape of the circle
View Solution
Knowledge Check
A piece of wire is bent in the shape of a parabola y=Kx2 (y - axis vorical) with a bead of mass m on it . The beat can side on the wire without friction , it stays the wire is now accleated parallel to the bead , where the bead can stay at rest with repect to the wire from the y - axis is
AagkBa2gkC2agkDa4gkA straight wire carrying current is parallel to the y-axis as shown in Fig. The
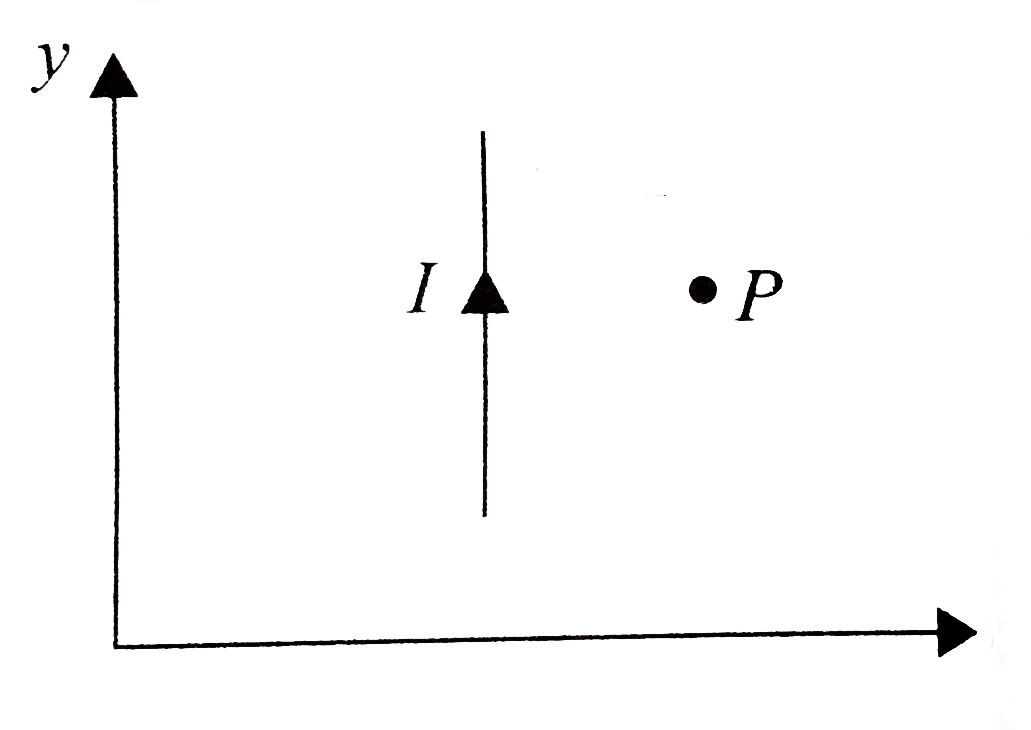 Amagnetic field at the point P is parallel to the x-axis.Bmagnetic field at P is along z-axisCmagnetic field are concentric circle with the wire passing through their common centreDmagnetic fields to the left and right of the wire and oppositely directed.
Amagnetic field at the point P is parallel to the x-axis.Bmagnetic field at P is along z-axisCmagnetic field are concentric circle with the wire passing through their common centreDmagnetic fields to the left and right of the wire and oppositely directed.A wire frame ABCD has a soap film. The wire BC can slide on the frame without friction and it is in equilibrium in the position shown in the figure. Find m, if T is the surface tension of the liquid.
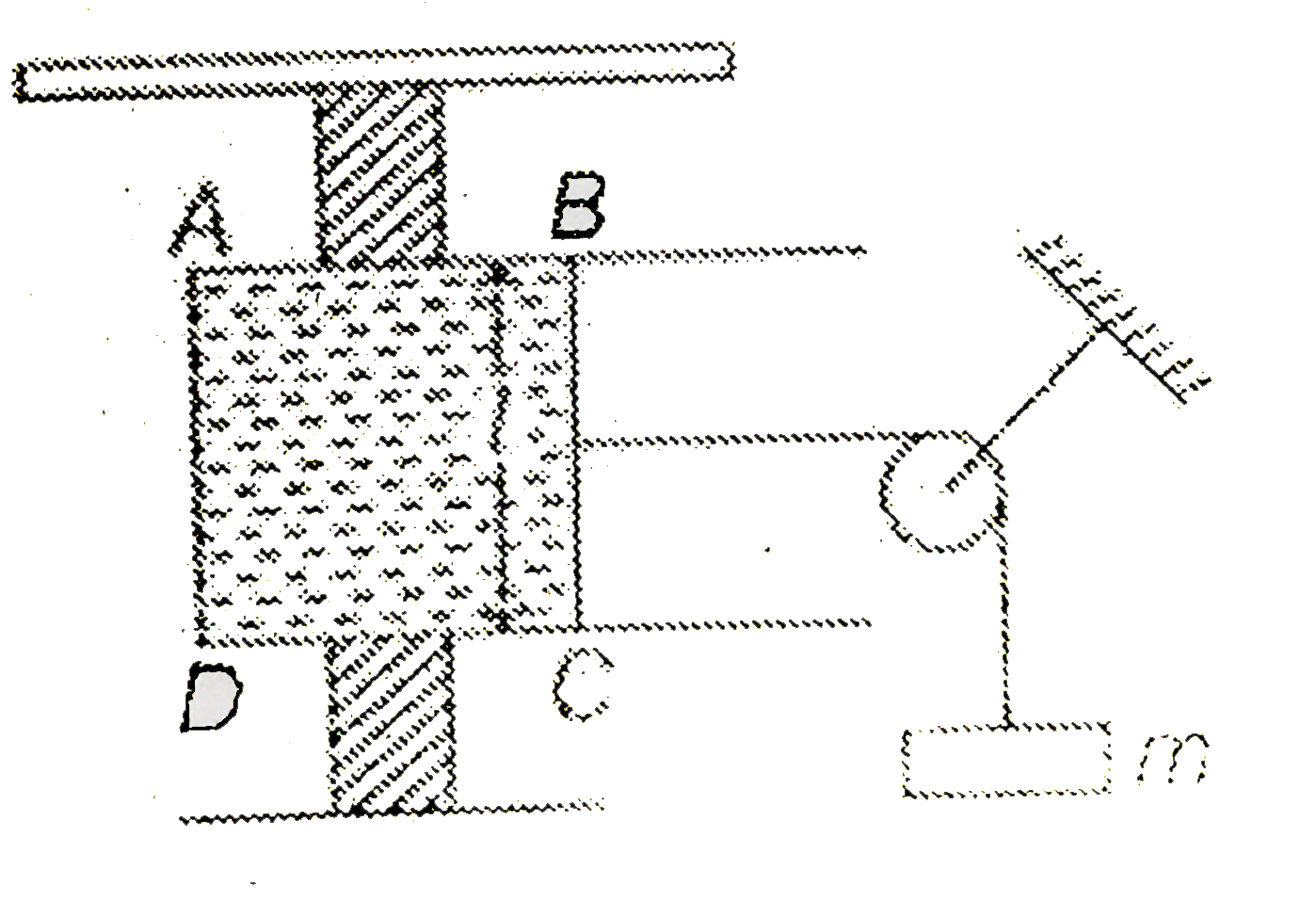 A2TlgBTlgCTl22gDTl2g
A2TlgBTlgCTl22gDTl2g
A pearl of mass m is in a position to slide over a smooth wire .At the intial instant the pearl is in the middle of the wire ,The wire moves linerly in a horizontal plane with an with the acceleration of the pearl Q.r.t wire is -

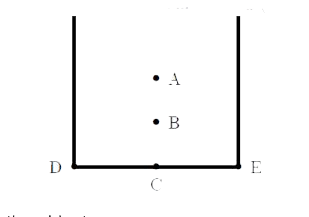
View SolutionA thick uniform wire is bent into the shape of the letter “U” as shown. Which point indicates the location of the center of mass of this wire?
View SolutionA wire which is bent in the shape of a curve given by, y=a3x4. A bead of mass m is located at point P(x,y). If the wire is smooth, find ω with which wire needs to be rotated for bead to be static.
View SolutionA thick uniform wire is bent into the shape of the letter "U" as shown. Which point indicates the location of the center of mass of this wire ? A is the midpoint of the line joining mid points of two parallel sides of 'U' shaped wire.
View SolutionA bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equastion is x2=4ay. The wire frame is fixed and the bead is released from the point y=4a on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by y=a is

View Solution
