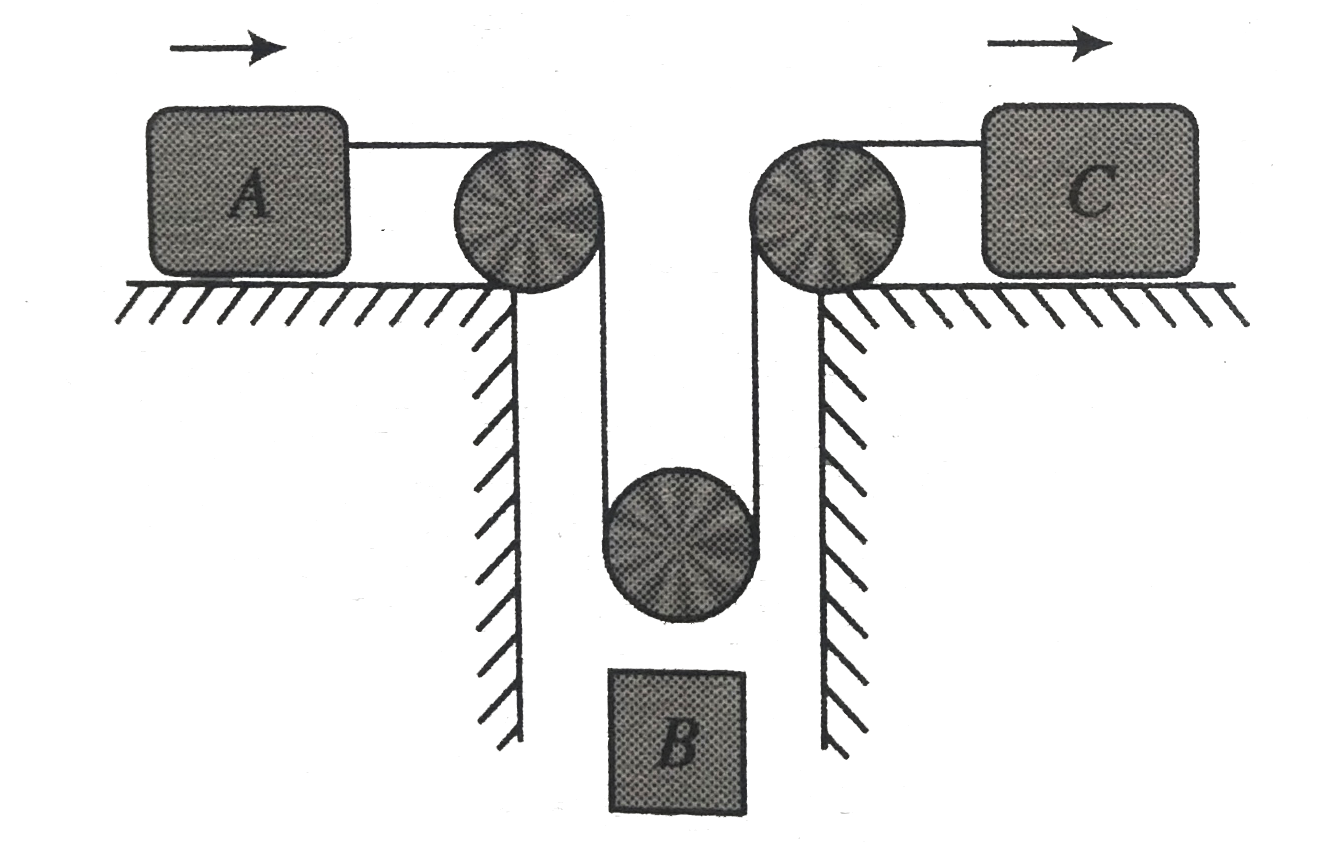
Block A and C start from rest and move to the right with acceleration $a_{A} = 12 t m / s^{2}$ and $a_{C} = 3 m / s^{2}$ Here t is in seconds. The time when block B attain comes to rest is:

A

2s

B

1s

C

$3 / 2 s$

D

$1 / 2 s$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

From contraint relation we can see that acceleration
block B is $a_{B} = (\frac{a_{A} + a_{C}}{2})$ with proper signs Hence
$a_{B} = (\frac{3 - 12 t}{2}) = 1.5 - 6 t or \frac{d v_{B}}{d t} = 1.5 - 6 t$
or $v_{B} \int 0 d v_{B} = t \int 0 (1.5 - 6 t) d t or v_{B} = 1.5 t - 3 t^{2}$
or $v_{B} = 0 at t = \frac{1}{2} s$

|

Updated on:21/07/2023

Class 11 PHYSICS NEWTONS LAW OF MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Block A and C starts from rest and move to the right with acceleration $a_{A} = 12 t m s^{- 2}$ and $a_{C} = 3 m s^{- 2}$ . Here t is in second. The time when block B again comes to rest is

A2s
B1s
C $3 / 2 s$
D $1 / 2 s$
Question 2 - Select One
Blocks $m_{1}$ and $m_{2}$ starts from rest and move to right with accelerations as shown. If $t$ is in second then the time when block $m_{3}$ again come to rest from $t = 0$ is (pulley and strings are ideal) :
.
A $\frac{\sqrt{5}}{2} sec$
B $\frac{1 + \sqrt{5}}{2} sec$
C $\frac{1 + \sqrt{3}}{2} sec$
D $1 sec$
Question 3 - Select One
Two particles A and B start from rest at the origin $x = 0$ and move along a straight line such that $a_{A} = (6 t - 3) m s^{- 2}$ and $a_{B} = (12 t^{2} - 8) m s^{- 2}$ where t is in seconds based on the above facts answer the following questions,
Total distance travelled by B at $t = 4$ s is
A192 m
B184 m
C196 m
D200m

GRB PUBLICATION-FORCE AND NEWTONS LAWS OF MOTION-Objective Questions

Home
Ask Doubt
Profile