A plane EM wave travelling in vacuum along z - direction is given by →E=E0sin(kz−ωt)ˆi and →B=B0sin(kz−ωt)ˆj.
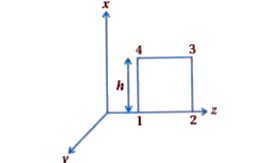
Use equation ∫→E.→dl=−dϕBdt to prove E0B0=c. Solution in Gujrati
Now ∮→E.→dl=−ddt∮→B.→ds
thereoe From equation (1) and (2),
E0h[sin(kz2−ωt)−sin(kz1−ωt)]=−ddt
[B0hk{cos(kz2−ωt)−cos(kz1−wt)}]
∴E0h[sin(kz2−ωt)−sin(kz1−ωt)]
=B0hk(ω)[sin(kz2−ωt)−sin(kz1−ωt)]
∴E0h=R0h(ωk)
∴E0=B0c [∵ωk=c]
∴E0B0=c
Topper's Solved these Questions
- ELECTROMAGNETIC WAVESBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - SECTION D MULTIPLE CHOICE QUESTIONS (MCQs)
76 Videos
- ELECTROMAGNETIC WAVESBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - SECTION D MULTIPLE CHOICE QUESTIONS (MCQs) MCQs asked in Competitive Exams
23 Videos
- ELECTROMAGNETIC WAVESBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - SECTION C NCERT EXEMPLAR SOLUTION (Short Answer Type Questions)
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D MCQs (MCQs asked in Competitive Exams )
38 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section D ( MCQs asked in Cometitive Exams )
39 Videos
Similar Questions
Maxwell's equations describe fundamental laws of …..
View SolutionMaximum value of magnetic field of progressive electromagnetic wave is 20 nT, then maximum value of electric field is ………
View SolutionShow that the magnetic field B at a point in between the plates of a parallel plate capacitor during charging is B=μ0∈0r2.dEdt (symbols having usual meaning).
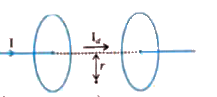
View SolutionThree pure inductance each of 3 H are connected as shown in figure. The equivalent inductance of this connection between points A and B is ......

View SolutionCapacitance of a capacitor 100 μ F. The work is done for depositing chargc 8×10−18 C on it will be .........
View SolutionIf ∣∣(a−x)2(a−y)2(a−z)2(b−x)2(b−y)2(b−z)2(c−x)2(c−y)2(c−a)2∣∣=0 and vectors →A,→B,and→C,where→A=a2ˆi+aˆj+ˆk , etc, are non-coplanar, then prove that vectors →X,→Yand→Z,where→X=x2ˆi+xˆj+ˆk , etc. may be coplanar.
View SolutionA vector →d is equally inclined to three vectors →a=ˆi+ˆj+ˆk,→b=2ˆi+ˆjand→c=3ˆj−2ˆk. Let→x,→y,and→z be thre vectors in the plane of →a,→b;→b,→c;→c,→a, respectively. Then →x.→d=−1 b. →y.→d=1 c. →z.→d=0 d. →r.→d=0,where→r=λ→x+μ→y+δ→z
View Solutionif vec u=hat i+hat j,vec v=hat i-hat j and vec w=hat i+2hat j+3hat k if vec n is unit vector such that vec u*vec n=0 and vec v.vec n=0 then find out |vec w*vec n|
View SolutionA plane EM wave travelling in vacuum along z-direction is given by E=E_(0) " sin "(kz- omegat) hati " and " B =B_(0) " sin " (kz- omegat) hatj (i) Evaluate intE. dl over the rectangular loop 1234 shown in figure. (ii) Evaluate int B.ds over the surface bounded by loop 1234. (iii) Use equation int E.dl = (-dphi_(B))/(dt) to prove (E_(0))/(B_(0)) =c. (iv) By using similar proces and the equation int B.dl =mu_(0) I+ epsilon_(0) (dphi_(E))/(dt), prove that c (1)/(sqrt(mu_(0) epsilon_(0))
View SolutionLet →u=ˆi+ˆj,→v=ˆi−ˆj and →w=ˆi+2ˆj+3ˆk . If ˆn is a unit vector such that →u.→n = 0 and →v.ˆn=0 then |→w.ˆn| is equal to.
View SolutionAn electromagnetic wave travels in vacuum along z - direction : →E=(E1ˆi+E2ˆj)cos(kz−ωt). Choose the correct options from the following :
View SolutionA plane EM wave travelling in vacuum along z - direction is given by vec(E )=E_(0)sin (kz - omega t)hat(i) and vec(B)=B_(0)sin(kz - omega t)hat(j) . Evaluate int vec(E ). Vec(d)l over the rectangular loop 134 shown in figure.
View SolutionA plane EM wave travelling in vacuum along z - direction is given by vec(E )=E_(0)sin (kz - omega t)hat(i) and vec(B)=B_(0)sin(kz - omega t)hat(j) . Evaluate int vec(B).vec(d)s over the surface bounded by loop 1234.
View SolutionA plane EM wave travelling in vacuum along z - direction is given by vec(E )=E_(0)sin (kz - omega t)hat(i) and vec(B)=B_(0)sin(kz - omega t)hat(j) . By using similar process and the equation int vec(B).vec(d)l = mu_(0)I+ in_(0)(d phi_(E ))/(dt) , prove that c=(1)/(sqrt(mu_(0)in_(0)))
View SolutionA plane EM wave travelling along z - direction is desctribed vec(E )=E_(0)sin(kz - omega t)hat(i) and veC(B)=B_(0)sin (kz - omega)hat(j) . Show that The average energy density of the wave is given by U_(av)=(1)/(4)in_(0)E_(0)^(2)+(1)/(4).(B_(0)^(2))/(mu_(0)) .
View Solution
