निर्वात में z दिशा के अनुदिश गमनशील एक समतल वैधुतचुबकीय तरंग को E=E0sin(kz−εt)ˆI तथा B=B0sin(kz−εt)ˆj द्वारा प्रदर्शित किया गया हैं
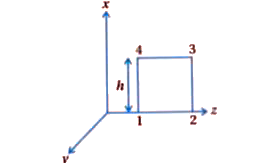
(i)चित्र में दर्शाइए गए आयताकार लूप 1234 पर ∫E.d1 का मान ज्ञात कीजिए
(ii) लूप 1234 द्वारा घिरे पुष्ठ के लिए ∫B.ds का मान ज्ञात कीजिए।
(iii) समीकरण ∫E.d1=−dϕBdt का उपयोग करके सिध्द कीजिए E0B0=c
(iv) इसी प्रकार की प्रकिया तथा समीकरण OB.d1=μ0I+E0dϕEdt का उपयोग करके सिध्द कीजिए कि c=1√μ0E0
(i)∫E.Dl=2∫1E.dl+3∫E.dl+4∫3E.dl+1E4.dl2
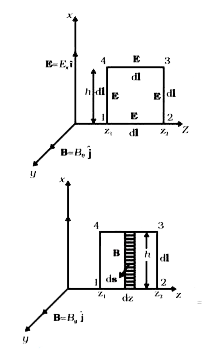
=2∫1E.dlcos90∘+3∫2E.dlcos)+4∫3E.dlcos90 (ii)∫B.s का मूल्यकान करने के लिए प्रतयेक से बने आयत 1234 पर विचार करें।
=−B0hk[cos(kz2−εt)–cos(kz1–εt)]
(iii) ∫E.dl=−dϕEdt
समीकरणों (1) तथा (2) में प्राप्त संबधों का उपयोग करके तथा सरलीकरण द्वारा हमे प्राप्त होगा।
E0h[sin(kz2–ε)−sin(kz1–εt)=B0hkε[sin(kz2−εt)–sin(kz1–εt)]
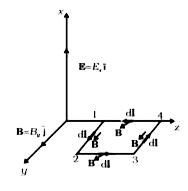
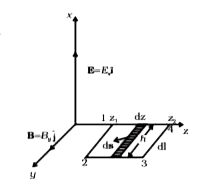
(iv) ∫B.dl के मूल्यकान के लिए लिए लूप 1234 पर yz तल में चित्र द्वारा दर्शाए अनुसार विचार करें।
=2∫1B.dlcos0+3∫2Bdlcos90∘+4∫3Bdlcos180∘+4–1∫Bdlcos90∘
ϕE=∫E.ds का मूल्याकन करने के जिलए प्रत्येक क्षेत्र फल की पहियो से बने 1234 पर विचार करें।
=−E0hk[cos(kz2–εt)−cos(kz1–εt)]
dϕEdt=E0hεk[sz∈(kz1−εt)–sin(kz2–εt)
B.dl=μ0ε0.dϕEdt
सकमीरणों (3) तथा(4) मेंप्राप्त का उपयोग करके तथा सरल करने है।
B0–E0εk.μ0ε0
या़c.c=1μ0ε0अत:c=1√μ0ε0
Topper's Solved these Questions
Similar Questions
सोडियम के किसी तनु लक्ष्य (10−2m2 क्षेत्रफल, 10−3m मोटाई) पर विचार कीजिए जिस पर जब 100W/m2 तीव्रता का प्रकाश (λ=660nm) डाला जाता है तो इससे 100μA की प्रकाश विद्युत धारा उत्पन्न होती है। जब कोई इलेक्ट्रॉन किसी सोडियम परमाणु (Na का घनत्व 0.97kg/m3) से टकराता है तो फोटोइलेक्ट्रॉन उत्पन्न होने की प्राथमिकता परिकलित कीजिए।
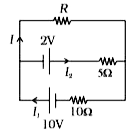
View Solutionदो सेल जिनकी वोल्टता 10Ω तथा 2V एवं आन्तरिक प्रतिरोध क्रमश: 10Ω तथा 5Ω हैं, पार्श्वक्रम में इस प्रकार संयोजित हैं कि 10v बैटरी का धनात्मक टर्मिनल 2V बैटरी के ऋणात्मक टर्मिनल से संयोजित है (चित्र 3.8)। संयोजन की प्रभावी वोल्टता तथा प्रभावी प्रतिरोध ज्ञात कीजिए।
View Solutionif E=E_(0)sin(kz-omegat) and B=B_(0)(kz-omegat) are electric and magnetic field produced by an electromagnetic wave travelling in +z direction in a medium. Then if eta=(E_(0))/(B_(0)) , then the value of eta is [mu =permeability of a medium epsilon= permittivity of medium]
View SolutionA plane EM wave travelling in vacuum along z-direction is given by E=E_(0) " sin "(kz- omegat) hati " and " B =B_(0) " sin " (kz- omegat) hatj (i) Evaluate intE. dl over the rectangular loop 1234 shown in figure. (ii) Evaluate int B.ds over the surface bounded by loop 1234. (iii) Use equation int E.dl = (-dphi_(B))/(dt) to prove (E_(0))/(B_(0)) =c. (iv) By using similar proces and the equation int B.dl =mu_(0) I+ epsilon_(0) (dphi_(E))/(dt), prove that c (1)/(sqrt(mu_(0) epsilon_(0))
View SolutionThe magnetic field of a plane electromagnetic wave is given by: →B=B0ˆi−[cos(kz−ωt)]+B1ˆjcos(kz+ωt) where B0=3×10−5T and B1=2×10−6T. The rms value of the force experienced by a stationary charge Q=10−4C at z=0 is close to:
View Solutionसिद्ध कीजिए की रेखा →r=2ˆi−2ˆj+3ˆk+t(ˆi−ˆj+4ˆk) समतल →r.(ˆi+5ˆj+ˆk)=5 के समान्तर है उसके बीच की दूरी ज्ञात कीजिए।
View Solutionयदि रेखा ¯r=(ˆi−2ˆj+ˆk)+λ(2ˆt+ˆj+2ˆk), समतल ¯r.(3ˆi−2ˆj+mˆk)=3 के समांतर हो तो m का मान ज्ञात कीजिए।
View Solutionसदिशों →a=2ˆi−ˆj+2ˆk और →b=−ˆi+ˆj+3ˆk के योगफल के अनुदिश मात्रक सदिश ज्ञात कीजिये।
View SolutionAn electromagnetic wave travels in vacuum along z - direction : →E=(E1ˆi+E2ˆj)cos(kz−ωt). Choose the correct options from the following :
View SolutionA plane EM wave travelling in vacuum along z - direction is given by vec(E )=E_(0)sin (kz - omega t)hat(i) and vec(B)=B_(0)sin(kz - omega t)hat(j) . Evaluate int vec(E ). Vec(d)l over the rectangular loop 134 shown in figure.
View SolutionA plane EM wave travelling in vacuum along z - direction is given by vec(E )=E_(0)sin (kz - omega t)hat(i) and vec(B)=B_(0)sin(kz - omega t)hat(j) . Evaluate int vec(B).vec(d)s over the surface bounded by loop 1234.
View SolutionA plane EM wave travelling in vacuum along z - direction is given by →E=E0sin(kz−ωt)ˆi and →B=B0sin(kz−ωt)ˆj.
Use equation ∫→E.→dl=−dϕBdt to prove E0B0=c.
View SolutionA plane EM wave travelling in vacuum along z - direction is given by vec(E )=E_(0)sin (kz - omega t)hat(i) and vec(B)=B_(0)sin(kz - omega t)hat(j) . By using similar process and the equation int vec(B).vec(d)l = mu_(0)I+ in_(0)(d phi_(E ))/(dt) , prove that c=(1)/(sqrt(mu_(0)in_(0)))
View SolutionA plane EM wave travelling along z - direction is desctribed vec(E )=E_(0)sin(kz - omega t)hat(i) and veC(B)=B_(0)sin (kz - omega)hat(j) . Show that The average energy density of the wave is given by U_(av)=(1)/(4)in_(0)E_(0)^(2)+(1)/(4).(B_(0)^(2))/(mu_(0)) .
View SolutionA plane EM wave travelling along z - direction is desctribed →E=E0sin(kz−ωt)ˆi and veC(B)=B0sin(kz−ω)ˆj. Show that
The time averaged intensity of the wave is given by Iav=12c∈0E20.
View Solution
