A plane mirror is placed at the bottom of a tank containing a liquid of refractive index μ. P is a small object at a height h above the mirror. An observes P and its image in the mirror. The apparent distance between two will be
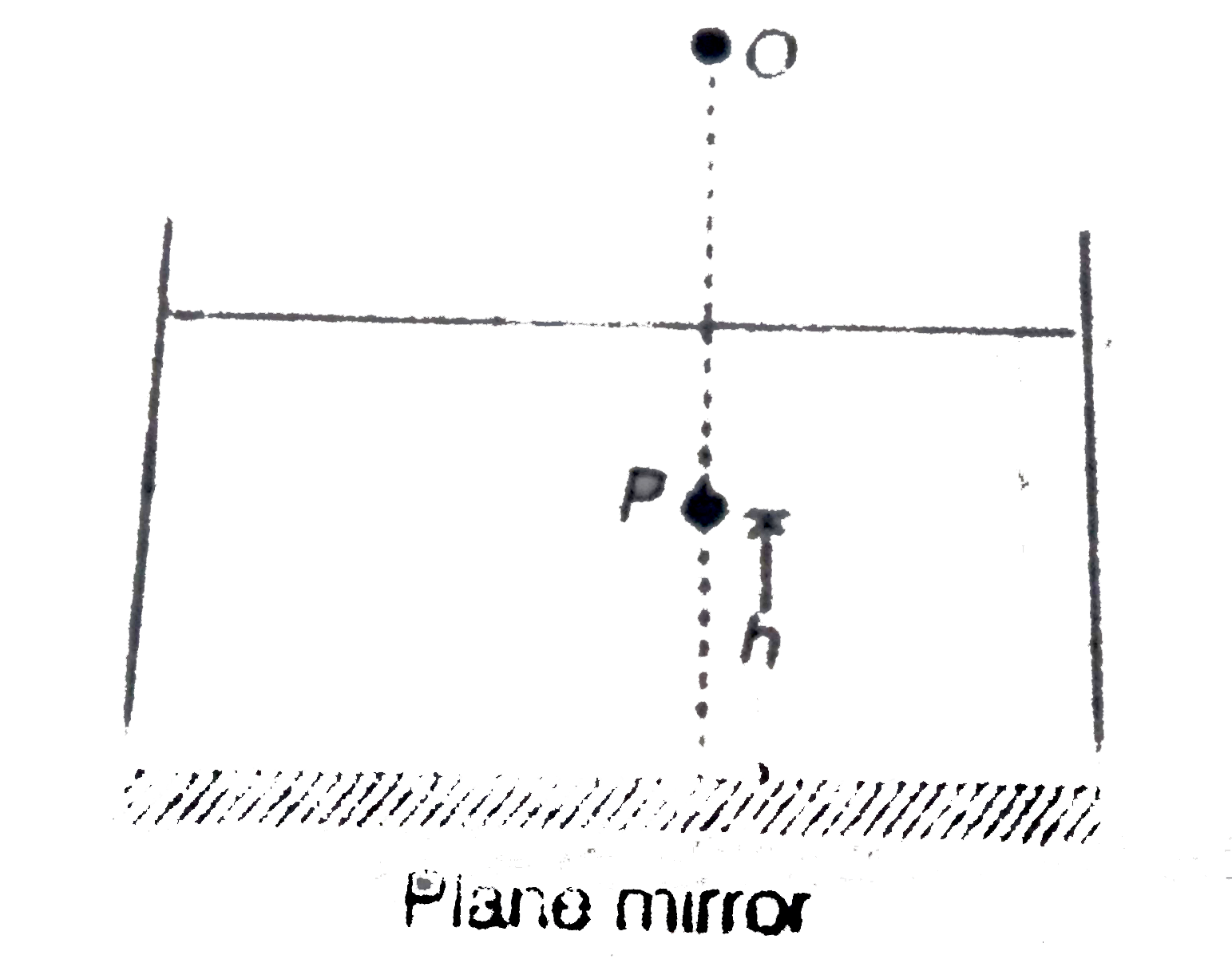
2μh
2hμ
2hμ−1
h(1+1μ)
The correct Answer is:B
Step by step video, text & image solution for A plane mirror is placed at the bottom of a tank containing a liquid of refractive index mu. P is a small object at a height h above the mirror. An observes P and its image in the mirror. The apparent distance between two will be by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - B. More than one option is correct
20 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - C. comprehension type question
14 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Integer type q.
15 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
Similar Questions
In Fig. a plane mirror lies at a height h above the bottom of a beaker containingwater (refractive index μ) upto a height f. Find the position of the image of the
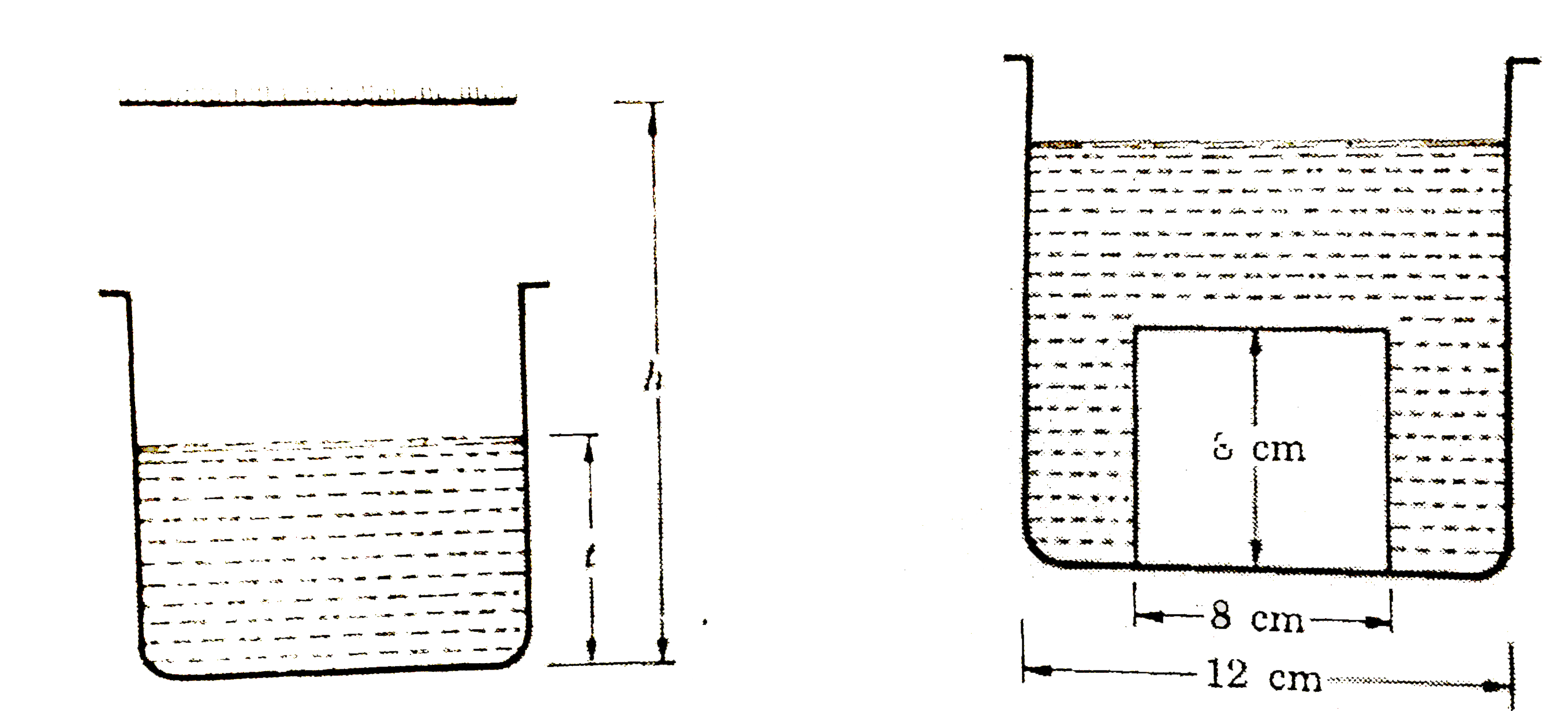
View SolutionAn object is placed at the bottom of a tank filled with liquid of refractive index 1.6. If the actual depth of the tank is 10 cm, what will be the apparent depth of the object?
View Solution
Knowledge Check
A plane mirror is placed at the bottom of the tank containing a liquid of refractive index μ. P is a small object at a height h above the mirror. An observer O-vertically above P outside the liquid see P and its image in the mirror. The apparent distance between these two will be:
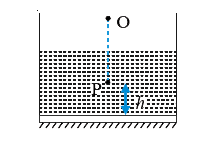 A2μhB2hμC2gμ−1Dh(1+1μ)
A2μhB2hμC2gμ−1Dh(1+1μ)A concave mirror of radius of curvature h is placed at the bottom of a tank containing a liquid of refractive index μ upto a depth d. An object P is placed at height h above the bottom of the miror. Outside the liquid, an observer O views the object and its image in the mirror. The apparent distance between these two will be
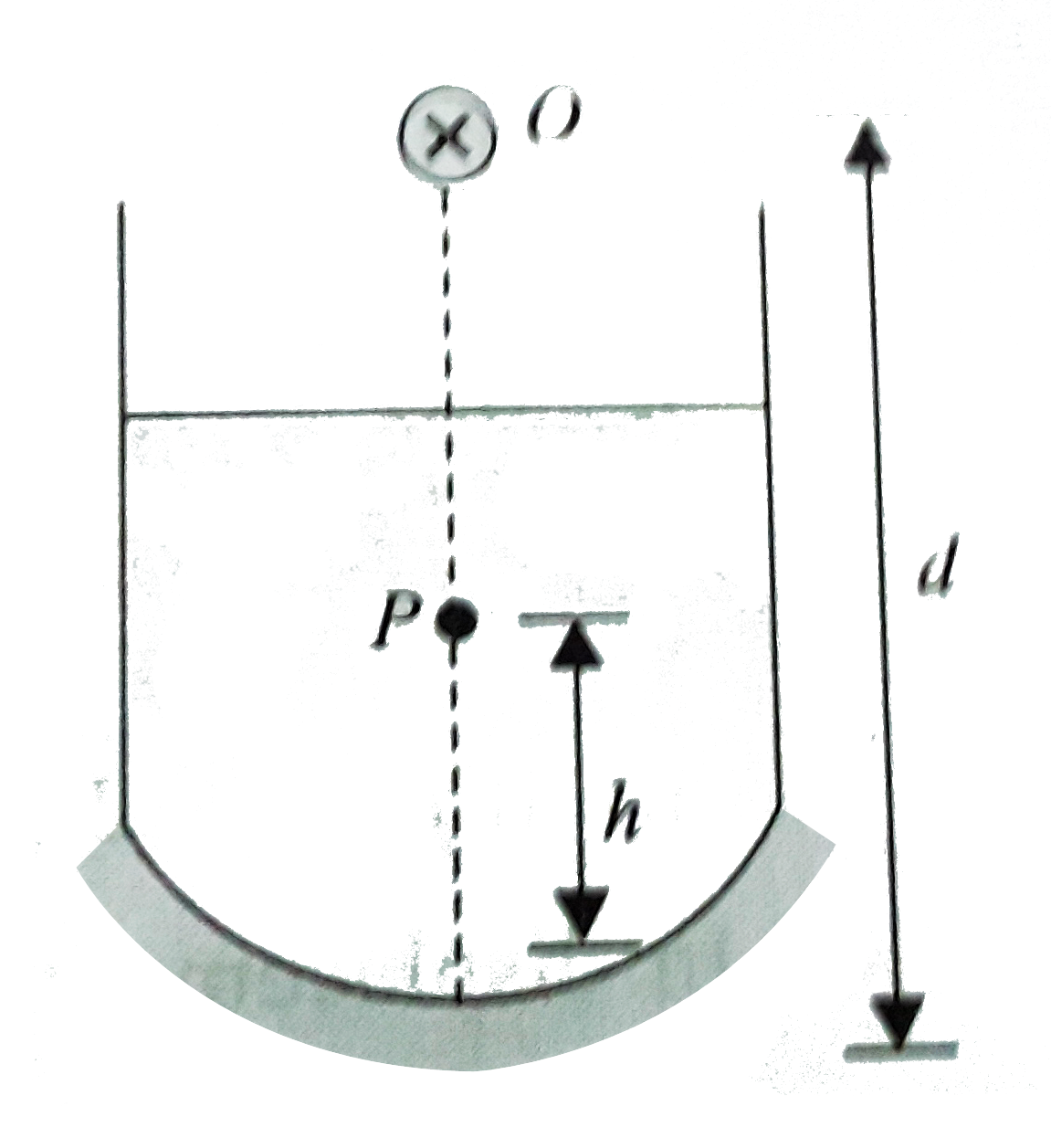 Ah(1−1μ)B2hμ−1CzeroD2hμ
Ah(1−1μ)B2hμ−1CzeroD2hμThere is a plane mirror at the bottom of tank filled with water having refractive index 4/3. A point object is placed at a height 10 cm above the bottom. What will be the apparent distance between point object and its image in plane mirror as observed by an observer outside the liquid in air ? Line joining observer and object is normal to the surface of water.
A10 cmB15 cmC20 cmD25cm
A tank contains a transparent liquid of refractive index μ. The bottom of the tank is a plane mirror as shown. A person at P looks at an object O and its image in the mirror. The distance between the object and its image in the mirror as preceived by the person is
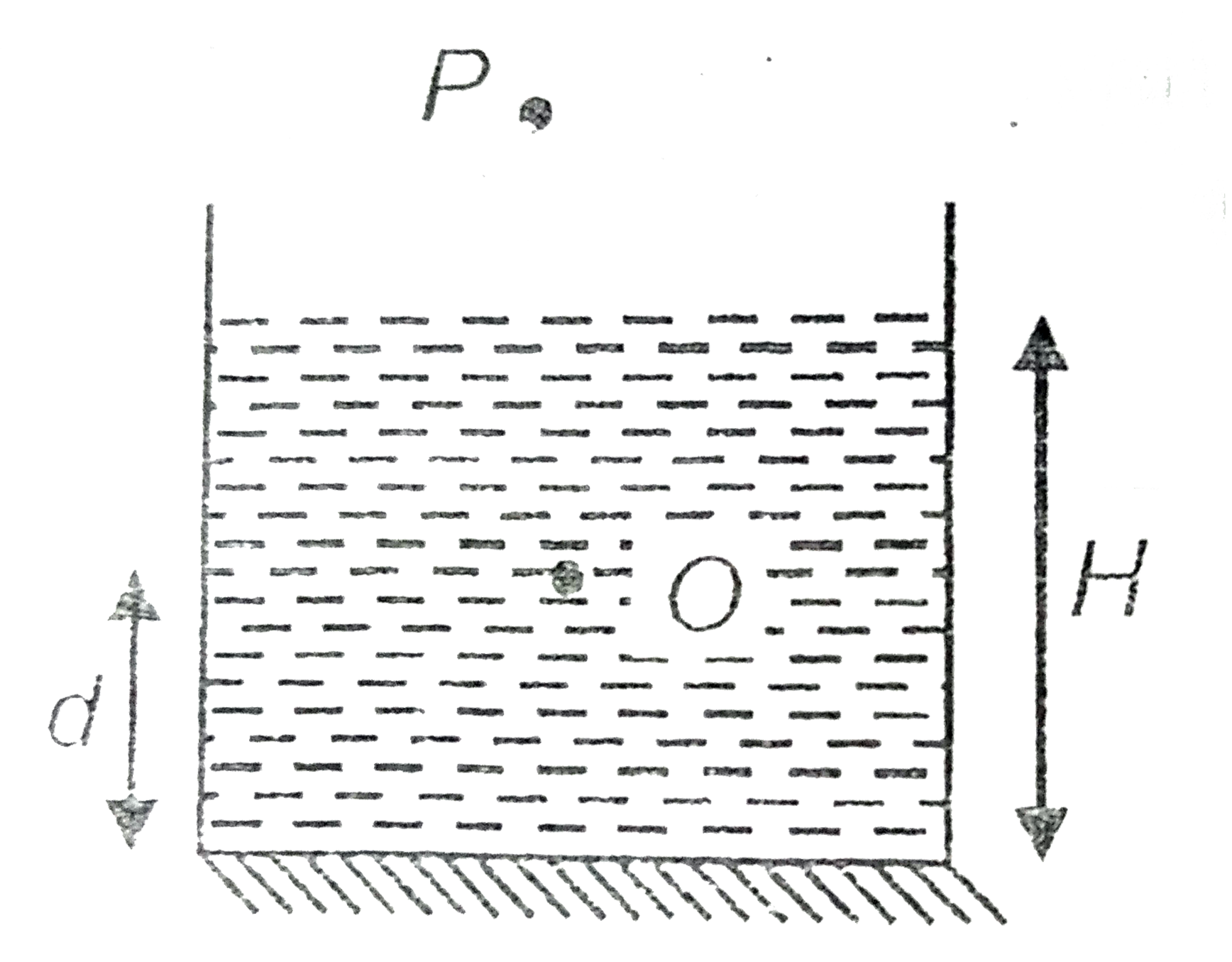
View SolutionA plane mirror is fixed at the bottom of a vessel as shown in the figure. Water of refractive index μ is filled up to a height h in the vessel. There is a fish at a height h/2 from bottom of vessel and there is a bird at a height h above the surface of water in the vessel.
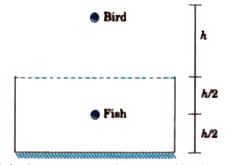
(a) Calculate apparent distance of bird as seen by the fish.
(b) Calculate apparent distance of image of bird in mirror as seen by the fish.
(c) Calculate apparent distance of fish as seen by the bird.
(d) Calculate apparent distance of image of fish in the mirror as seen by the bird.
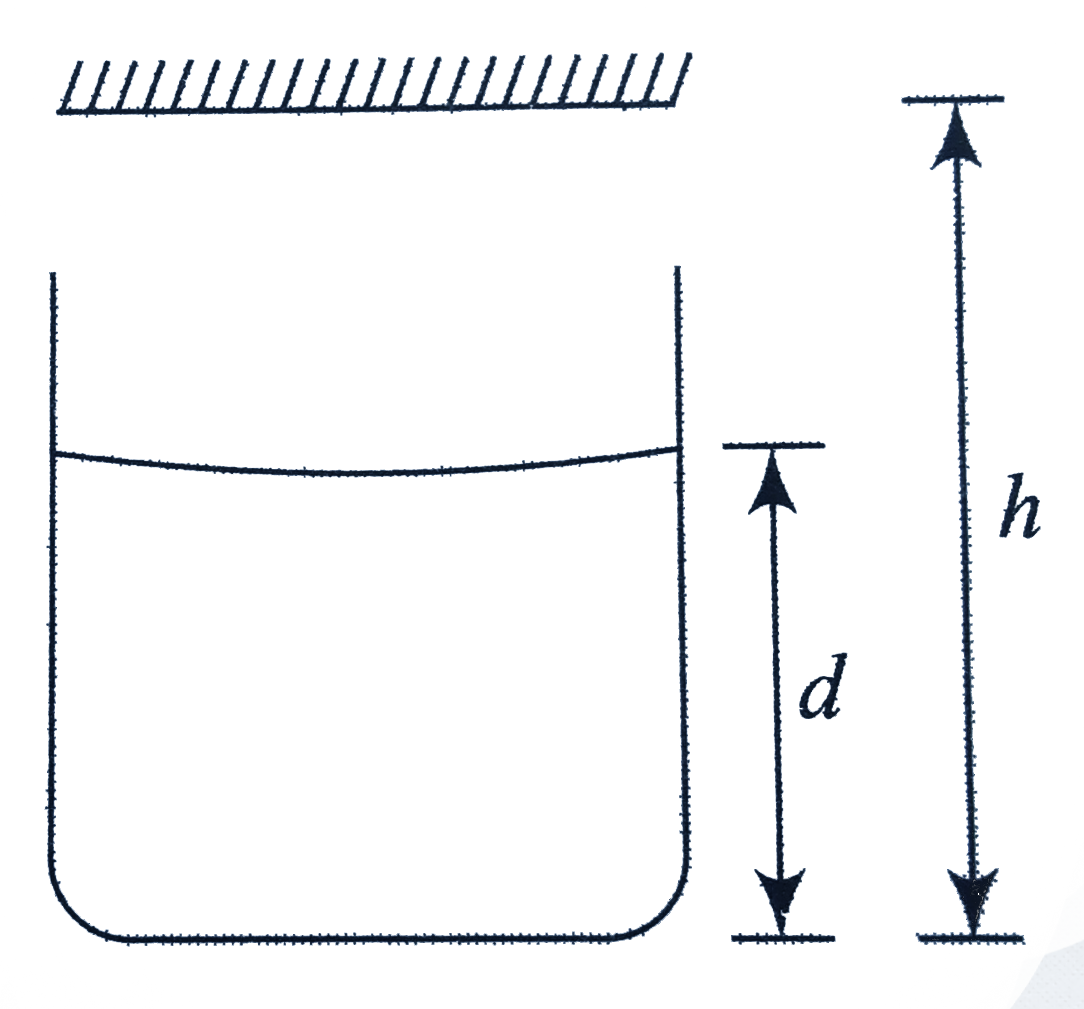
View SolutionConsider the situation shown in Figure. A plane mirror is fixed at a height h above the bottom of a beaker containing water (refractive index μ) upto a height d. Find the position of the image of bottom formed by the mirror.
View SolutionA plane mirror is placed at a distance of 50 cm from a concave mirror of focal length 16 cm. Where should a short object be placed between the mirrors and facing both the mirrors so that its virtual image in the plane mirror coincides with the real image in concave mirror? What is the ratio of the sizes of the two images?
View SolutionA point luminous object (O) is at a distance h from front face of a glass slab of width d and of refractive index μ. On the back face of slab is a refracting plane mirror. An observer sees the image of object in mirror as shown in figure. Distance of image from front face as seen by observer will be

View Solution
