A planet revolves around the sun in an elliptical orbit. If vp and va are the velocities of the planet at the perigee and apogee respectively, then the eccentricity of the elliptical orbit is given by :
vpva
va−vpva+vp
vp+vavp−va
vp−vavp+va
The correct Answer is:D
To find the eccentricity of the elliptical orbit of a planet revolving around the Sun, we can follow these steps:
1. Understanding the Orbit:
- The planet moves in an elliptical orbit around the Sun, with the closest point being the perigee (P) and the farthest point being the apogee (A).
- Let vp be the velocity at perigee and va be the velocity at apogee.
2. Identifying Distances:
- Let RP be the distance from the Sun to the planet at perigee and RA be the distance from the Sun to the planet at apogee.
- In terms of semi-major axis a and the distance from the center to the focus c (where the Sun is located), we have:
- RP=a−c
- RA=a+c
3. Conservation of Angular Momentum:
- The angular momentum L of the planet is conserved, so we can write:
mRPvP=mRAvA
- Here, m is the mass of the planet, which cancels out:
RPvP=RAvA
4. Expressing Velocities:
- Rearranging the above equation gives:
vPvA=RARP
5. Substituting Distances:
- Substitute the expressions for RA and RP:
vPvA=a+ca−c
6. Relating Eccentricity:
- The eccentricity e of the orbit is defined as:
e=ca
- We can express c in terms of a and e:
c=ae
7. Substituting for c:
- Substitute c=ae into the velocity ratio:
vPvA=a+aea−ae
- Simplifying gives:
vPvA=a(1+e)a(1−e)=1+e1−e
8. Cross Multiplying:
- Cross-multiplying gives:
vP−evP=vA+evA
- Rearranging leads to:
vP−vA=e(vP+vA)
9. Solving for Eccentricity:
- Finally, we can isolate e:
e=vP−vAvP+vA
Final Result:
The eccentricity e of the elliptical orbit is given by:
e=vP−vAvP+vA
- The planet moves in an elliptical orbit around the Sun, with the closest point being the perigee (P) and the farthest point being the apogee (A).
- Let vp be the velocity at perigee and va be the velocity at apogee.
- Let RP be the distance from the Sun to the planet at perigee and RA be the distance from the Sun to the planet at apogee.
- In terms of semi-major axis a and the distance from the center to the focus c (where the Sun is located), we have:
- RP=a−c
- RA=a+c
- The angular momentum L of the planet is conserved, so we can write:
mRPvP=mRAvA
- Here, m is the mass of the planet, which cancels out:
RPvP=RAvA
- Rearranging the above equation gives:
vPvA=RARP
- Substitute the expressions for RA and RP:
vPvA=a+ca−c
- The eccentricity e of the orbit is defined as:
e=ca
- We can express c in terms of a and e:
c=ae
- Substitute c=ae into the velocity ratio:
vPvA=a+aea−ae
- Simplifying gives:
vPvA=a(1+e)a(1−e)=1+e1−e
- Cross-multiplying gives:
vP−evP=vA+evA
- Rearranging leads to:
vP−vA=e(vP+vA)
- Finally, we can isolate e:
e=vP−vAvP+vA
The eccentricity e of the elliptical orbit is given by:
e=vP−vAvP+vA
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Universal law of Gravitations14videos
GRAVITATION
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - The Gravitational constant8videos
GRAVITATION
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason10videos
KINETIC THEORY
Similar Questions
Knowledge Check
- Question 1 - Select One
A planet revolves in elliptical orbit around the sun. (see figure). The linear speed of the planet will be maximum at
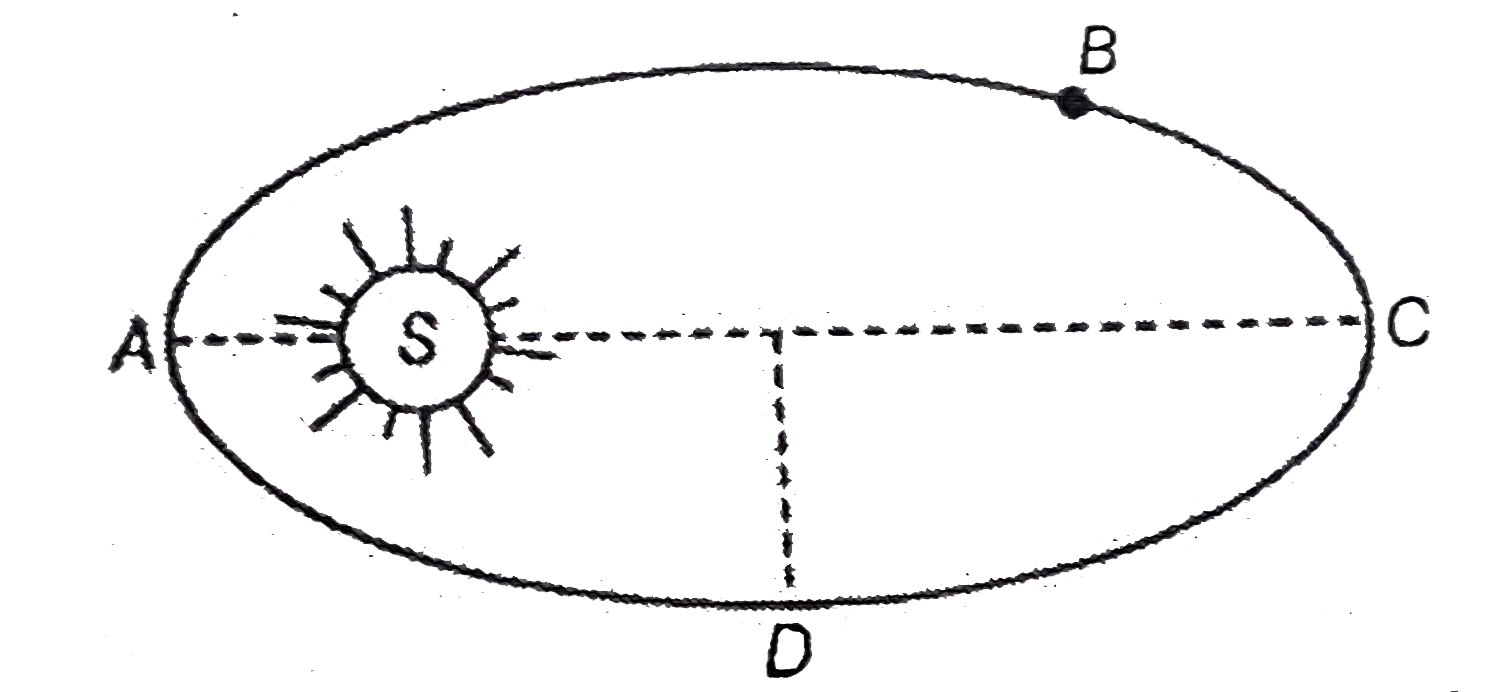 AABBCCDD
AABBCCDD - Question 2 - Select One
A planet orbits the sun in an elliptical path as shown in the figure. Let vp and vA be spped of the planet when at perohelion and aphelion respectively. Which of the following relations is correct ?
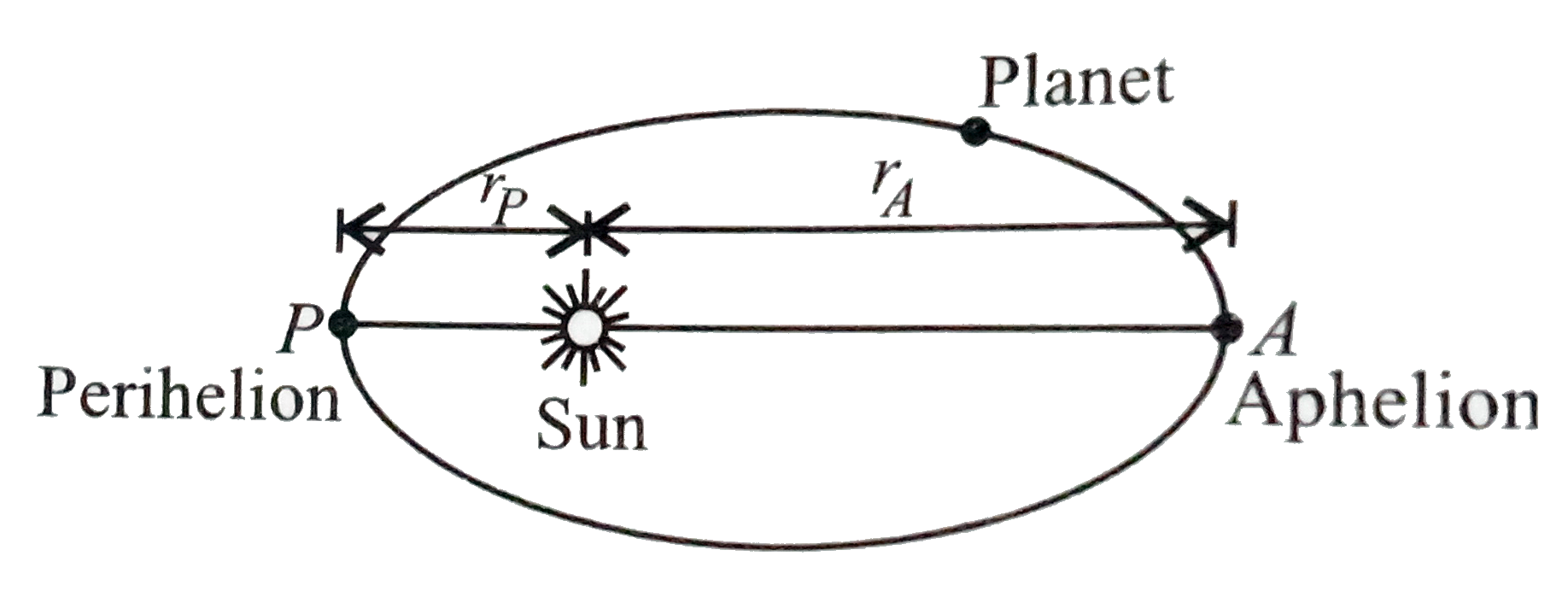 ArprA=vAvpBrprA=vpvACrprA=√vpvADrprA=√vAvp
ArprA=vAvpBrprA=vpvACrprA=√vpvADrprA=√vAvp
A planet revolves around the sun in an elliptical . The linear speed of the planet will be maximum at
 View Solution
View SolutionA planet is revolving round the sun in an elliptical orbit, If v is the velocity of the planet when its position vector from the sun is r, then areal velocity of the planet is
View SolutionA planet is revolving round the sun in an elliptical orbit as shown in figure. Select correct alternative(s)
View SolutionFor a planet revolving around Sun in an elliptical orbit, to obtain its velocity at any point we have to apply
View SolutionA planet is moving round the sun in an elliptical orbit as shows. As the planet moves from A to B
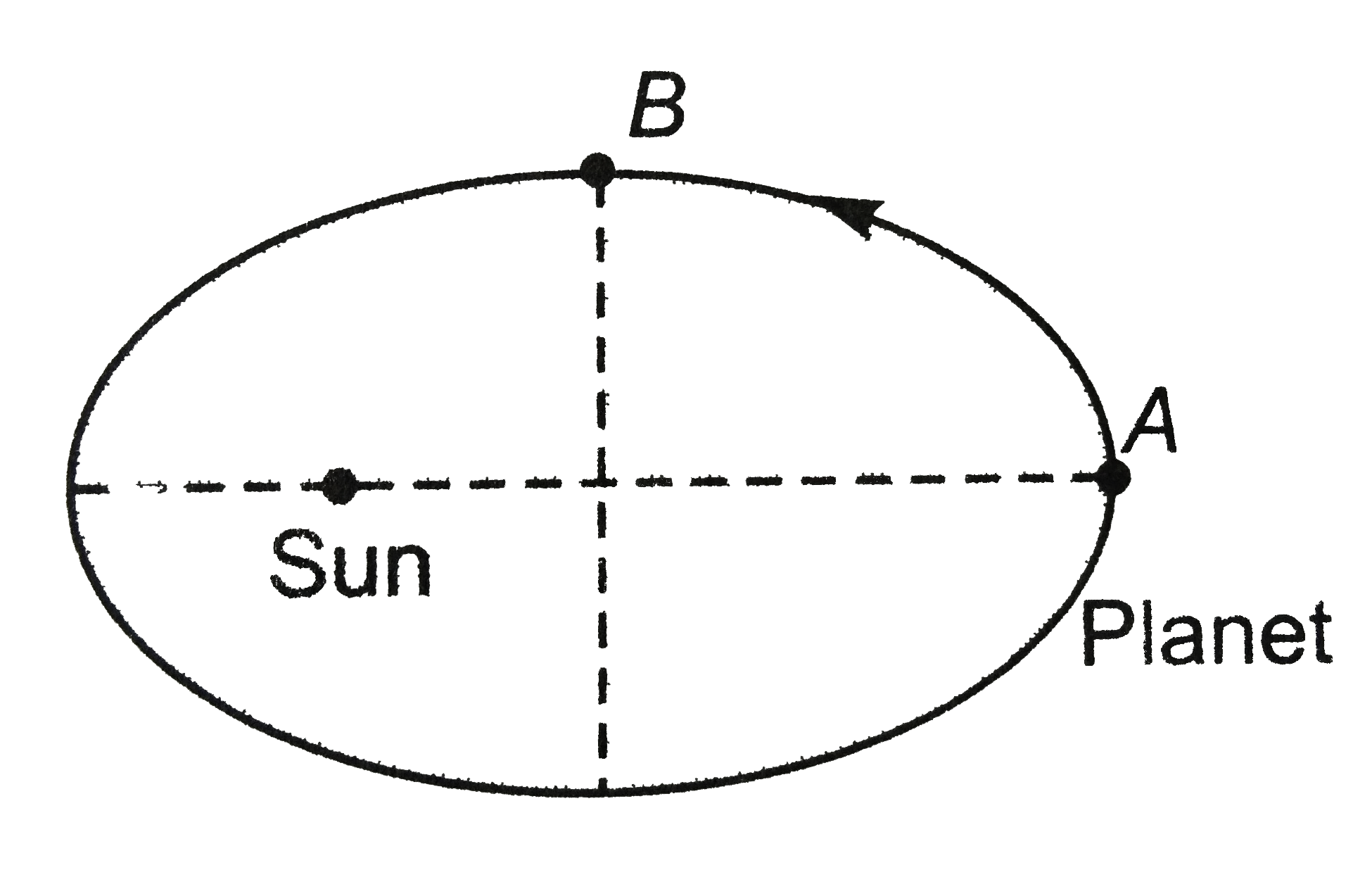 View Solution
View SolutionA planet revolves in elliptical orbit around the sun. (see figure). The linear speed of the planet will be maximum at
 View Solution
View Solution

