
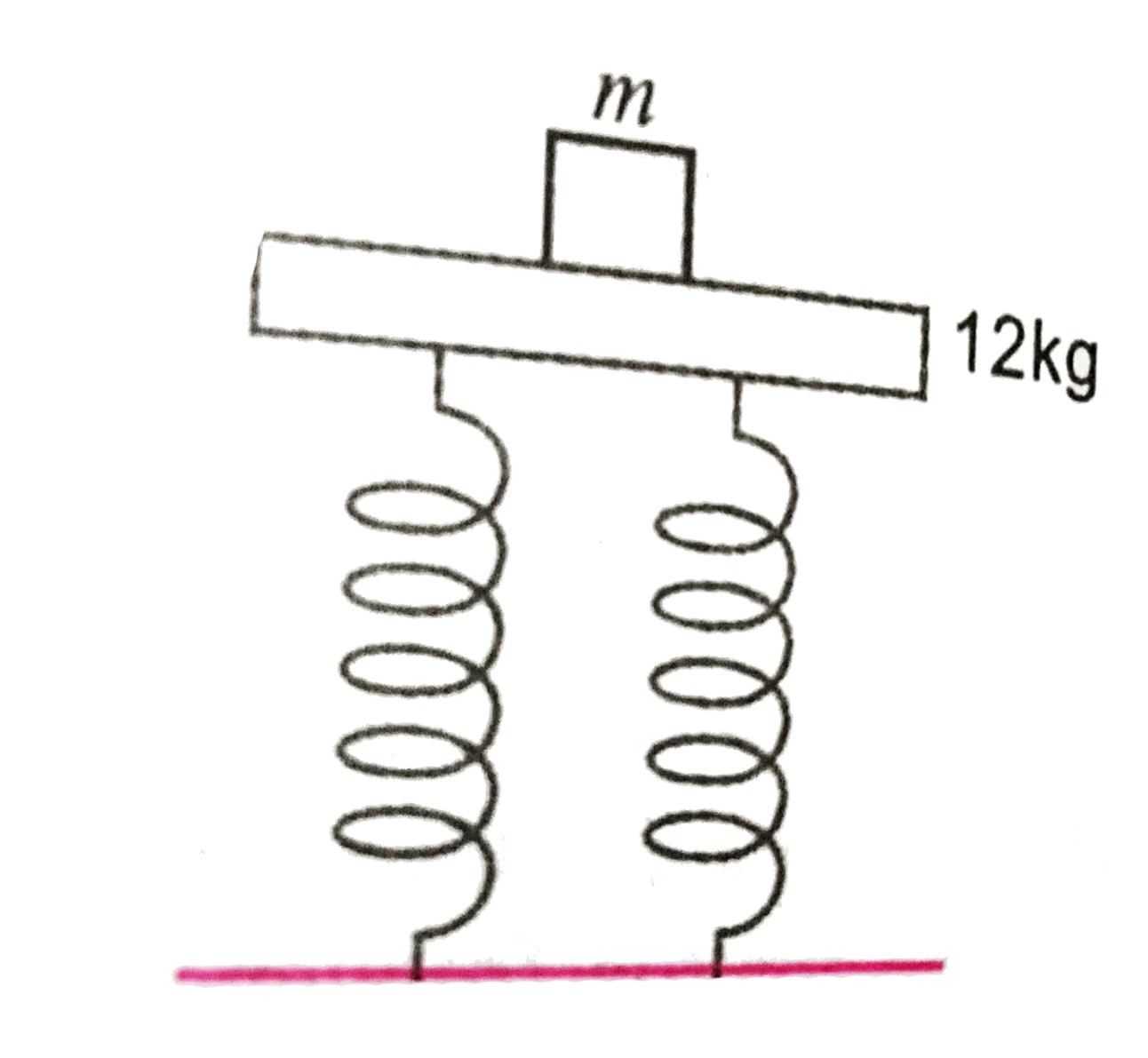
A plank of mass 12 kg is supported by two identical springs as shown is Fig. The plank always remains horizontal. When the plank is pressed down and released it performs simple harmonic motion with time period 3 s. When a block of m is attached to the plank the time priod changes to 6 s. The mass of the block is
48 kg
36 kg
24 kg
12 kg
The correct Answer is:B
Let spring constant of each spring be k then the equivalent spring constant of the two spring system in parallel is 2k
Without mass, T=3s=2π√122k
With mass, T1=65=2π√12+m2k
TT1=12=√1212+m
m=36kg
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A tray of mass 12 kg is supported by two identical springs as shown in figure. When the tray is pressed down slightly and released, it executes SHM with a time period of 1.5s. What is the force constant of each spring?When a block of mass m is placed on the tray , the period of SHM changes to 3.0s. What is the mass of the block ?
View SolutionAn arrangement of three identical spring and a block of mass 10 kg is shown in the adjoining figure. When the platform on which block is placed is slightly pressed down and released. It performs S.H.M. with a period of 2 s.
(i) Calculate the spring constant of the spring.
(ii) If a block of mass m is further placed on the platform, the new period of S.H.M. becomes 3.5 s. Find the value of m. (Assume platform to be massless)

View Solution
Knowledge Check
When a mass m attached to a spring it oscillates with period 4s. When an additional mass of 2 kg is attached to a spring, time period increases by 1s. The value of m is :-
A3.5 kgB8.2 kgC4.7 kgD2.6 kgA plank of mass M is placed on a smooth hroizonal surface. Two light identical springs each of stiffness k are rigidly connected to structs at the ends of the plank as shown. When the spring are in their unextended position the distance between their free ends is 3l. a block of mass m is placed on the plank and pressed aganist one of the springs so that it is compressed by l. To keep the blocks at rest it is connected to the strut by means of a light string, initially the syetem is at rest. Now the string is burnt.
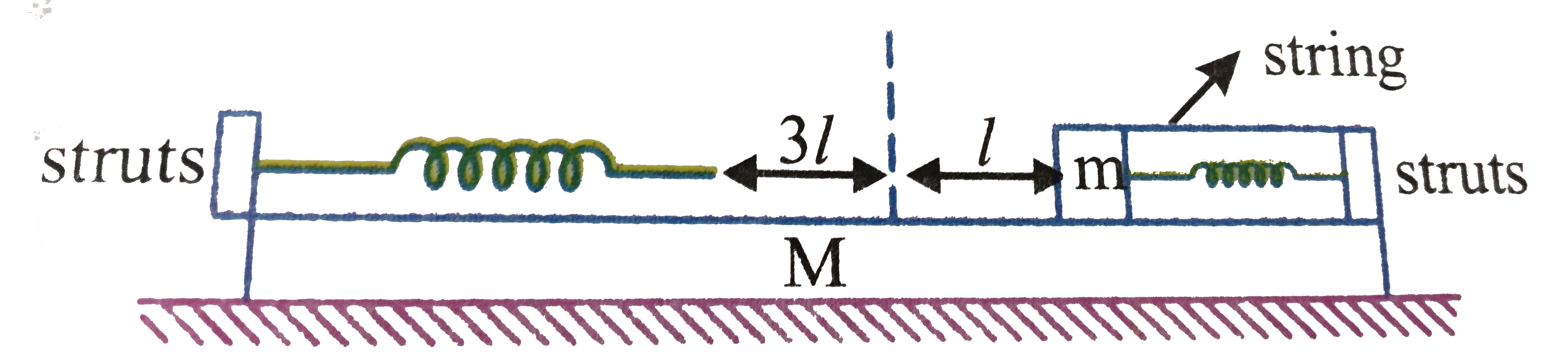
Time period of oscillation of block:A(2π+3)√2Mnk(M+m)B(π+6)√2Mnk(M+m)C(π+3)√Mmk(M+m)D(2π+6)√Mmk(M+m)A plank of mass M is placed on a smooth hroizonal surface. Two light identical springs each of stiffness k are rigidly connected to structs at the ends of the plank as shown. When the spring are in their unextended position the distance between their free ends is 3l. a block of mass m is placed on the plank and pressed aganist one of the springs so that it is compressed by l. To keep the blocks at rest it is connected to the strut by means of a light string, initially the syetem is at rest. Now the string is burnt.

Maximum displacement of plank is:Amlm+MB5mlm+MC3mlm+MD2mlm+M
A plank of mass 10 kg and a block of mass 2 kg are placed on a horizontal plane as shown in the figure. There is no friction between plane and plank. The coefficient of friction between block and plank is 0.5 .A force of 60 N is applied on plank horizontally. In first 2 s the work done by friction on the block is

View SolutionA horizontal plank has a rectangular block placed on it. The plank starts oscillating vertically and simple harmonically with an amplitude of 40 cm. The block just loses contact with the plank when the latter is at momentary rest Then.
View SolutionAccording to the principle of conservation of linear momentum if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
A plank of mass M is placed on a smooth horizontal surface. light identical springs, each of stiffness K, are rigidly connected to struts at the end of the plank as shown in Fig. When the springs are in their unextended position, the distance between their free ends is 3l. A block of mass m is placed on the plank and pressed against one of the springs so that it is compressed to l. To keep the block at rest it is connected to the strut means of a light string. Initially, the system is at rest, Now the string is burnt.

The maximum velocity of the plank is
View SolutionAccording to the principle of conservation of linear momentum if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
A plank of mass M is placed on a smooth horizontal surface. light identical springs, each of stiffness K, are rigidly connected to struts at the end of the plank as shown in Fig. When the springs are in their unextended position, the distance between their free ends is 3l. A block of mass m is placed on the plank and pressed against one of the springs so that it is compressed to l. To keep the block at rest it is connected to the strut means of a light string. Initially, the system is at rest, Now the string is burnt.
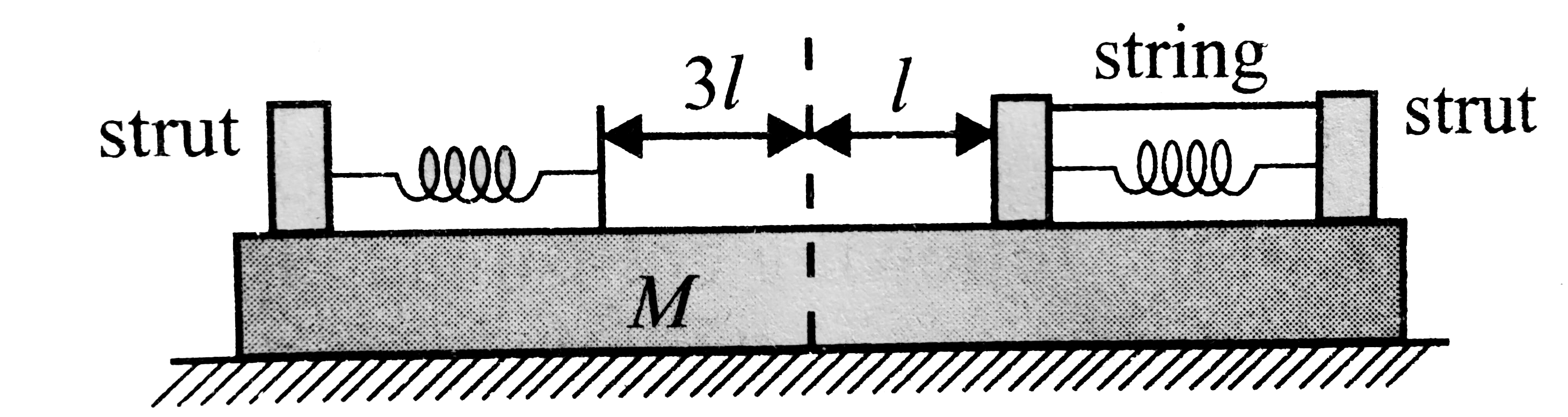
The maximum displacement of the plank is
View SolutionAccording to the principle of conservation of linear momentum if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
A plank of mass M is placed on a smooth horizontal surface. light identical springs, each of stiffness K, are rigidly connected to struts at the end of the plank as shown in Fig. When the springs are in their unextended position, the distance between their free ends is 3l. A block of mass m is placed on the plank and pressed against one of the springs so that it is compressed to l. To keep the block at rest it is connected to the strut means of a light string. Initially, the system is at rest, Now the string is burnt.
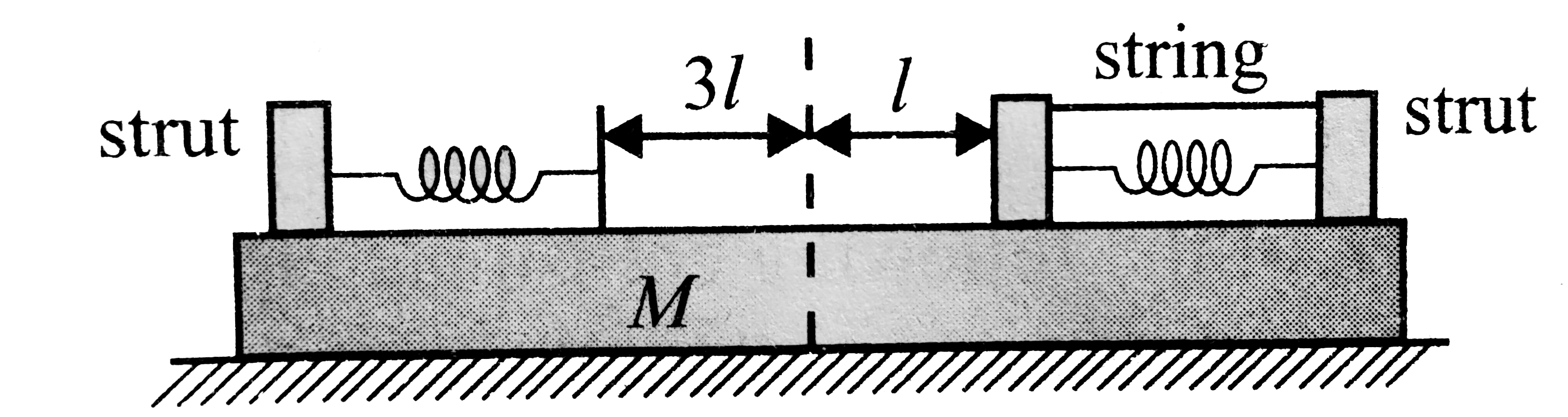
The maximum kinetic energy of the block m is
View Solution
