A plastic rod has been formed into a circle of radius R. It has a positive charge $+ Q$ uniformly distributed along one-quarter of its circumference and a negative charge of $- 6 Q$ uniformly distributed along the rest of the circumference (figure). With V = 0 at infinity, what is the electric potential $- 6 Q$
(a) at the centre C of the circle and
(b) at point P, which is on the central axis of the circle at distance z from the centre?

Video Solution

Answer

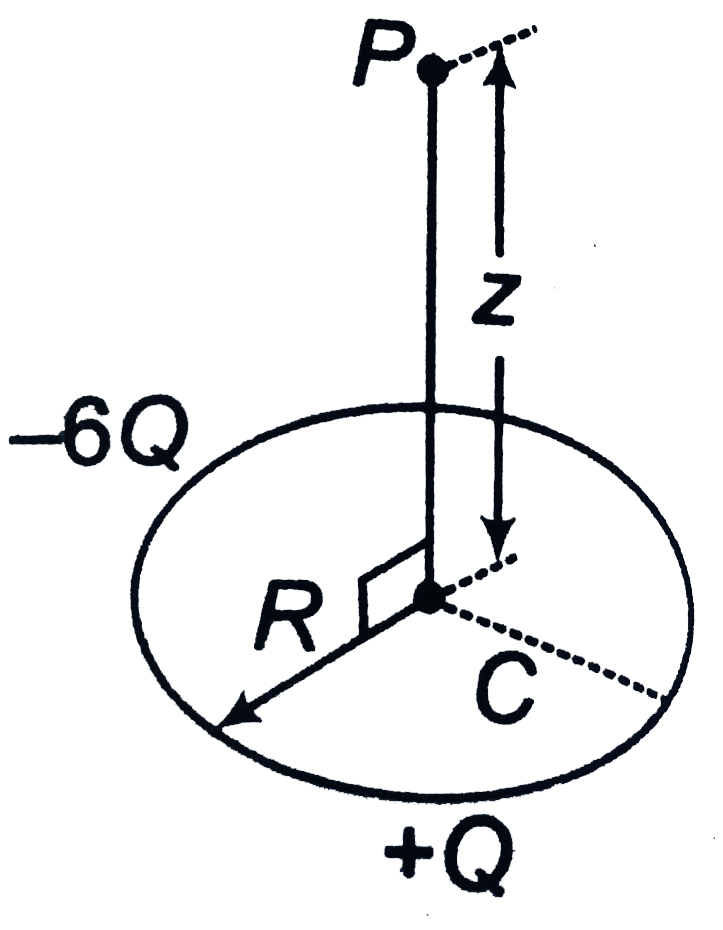
Step by step video & image solution for A plastic rod has been formed into a circle of radius R. It has a positive charge +Q uniformly distributed along one-quarter of its circumference and a negative charge of -6Q uniformly distributed along the rest of the circumference (figure). With V = 0 at infinity, what is the electric potential -6Q (a) at the centre C of the circle and (b) at point P, which is on the central axis of the circle at distance z from the centre? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Knowledge Check

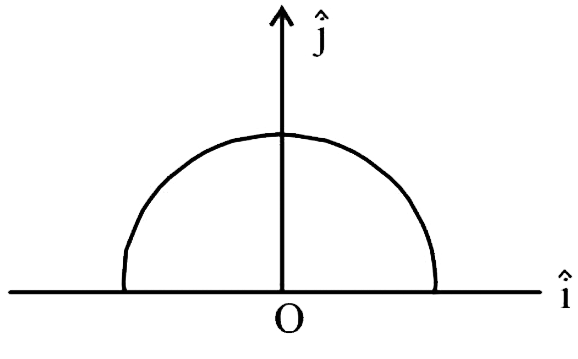
A thin glass rod is bent into a semicircle of radius r. A charge +Q is uniformly distributed along the lower half, as shown in fig. The electric field E at P, the center of the semicircle, is

A $\frac{Q}{π^{2} ε_{0} r^{2}}$
B $\frac{2 Q}{π^{2} ε_{0} r^{2}}$
C $\frac{4 Q}{π^{2} ε_{0} r^{2}}$
D $\frac{Q}{4 π^{2} ε_{0} r^{2}}$
A thin semi-circular ring of radius r has a positive charge q distributed uniformly over it. The net field $\to E$ at the centre O is

A(a) $\frac{q}{4 π^{2} ε_{0} r^{2}} ˆ j$
B(b) $- \frac{q}{4 π^{2} ε_{0} r^{2}} ˆ j$
C(c) $- \frac{q}{2 π^{2} ε_{0} r^{20} ˆ j}$
D(d) $\frac{q}{2 π^{2} ε_{0} r^{2}} ˆ j$