Question

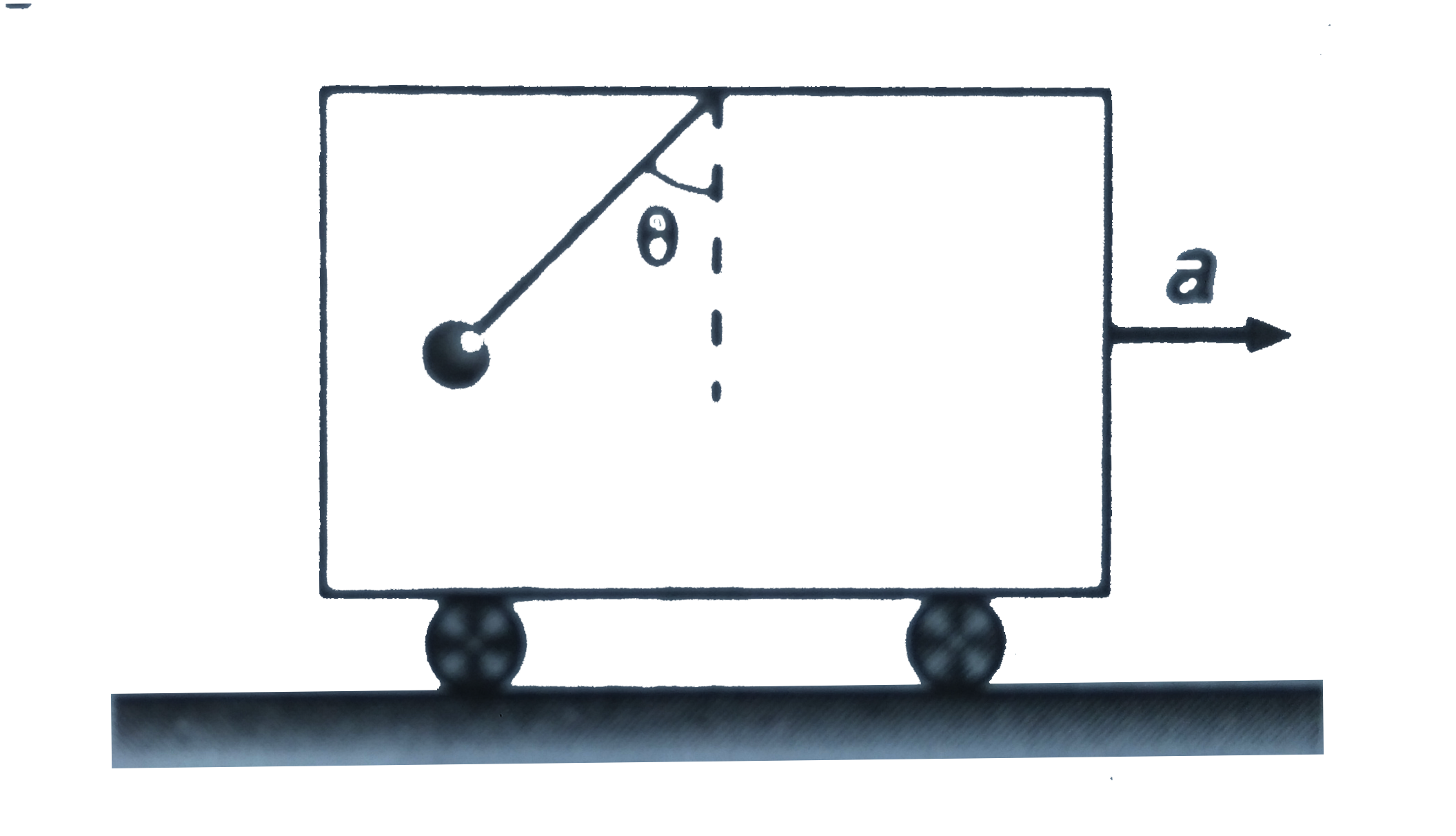
A plumb line is suspended from a ceiling of a car moving with horizontal acceleration of a . What will be the angle of inclination with vertical

Options

A. `tan^(-1)(a//g)`
B. `tan^(-1)(g//a)`
C. `cos^(-1)(a//g)`
D. `cos^(-1)(g//a)`

Answer

A

Explanation

To find the angle of inclination of a plumb line suspended from a ceiling of a car moving with a horizontal acceleration $$A$$, we can analyze the forces acting on the plumb line.

1. Identify the Forces:
- The weight of the plumb line acts vertically downward with a force \( W = mg \), where \( m \) is the mass of the plumb line and \( g \) is the acceleration due to gravity.
- The tension \( T \) in the string acts along the string, directed towards the point of suspension.

2. Establish the Coordinate System:
- Let the angle of inclination of the plumb line with the vertical be \( \theta \).
- The horizontal acceleration \( A \) of the car will create an inertial force acting on the plumb line in the opposite direction (to the left if the car accelerates to the right).

3. Draw a Free Body Diagram:
- The vertical component of the tension \( T \) must balance the weight:
\( T \cos \theta = mg \)
- The horizontal component of the tension must balance the inertial force due to the car's acceleration:
\( T \sin \theta = ma \)

4. Divide the Equations:
- Dividing the second equation by the first gives:
\( \frac{T \sin \theta}{T \cos \theta} = \frac{ma}{mg} \)
- This simplifies to:
\( \tan \theta = \frac{a}{g} \)

5. Find the Angle:
- To find the angle \( \theta \), take the arctangent of both sides:
\( \theta = \tan^{-1}\left(\frac{a}{g}\right) \)

Final Answer:
The angle of inclination of the plumb line with the vertical is given by:
\( \theta = \tan^{-1}\left(\frac{a}{g}\right) \)