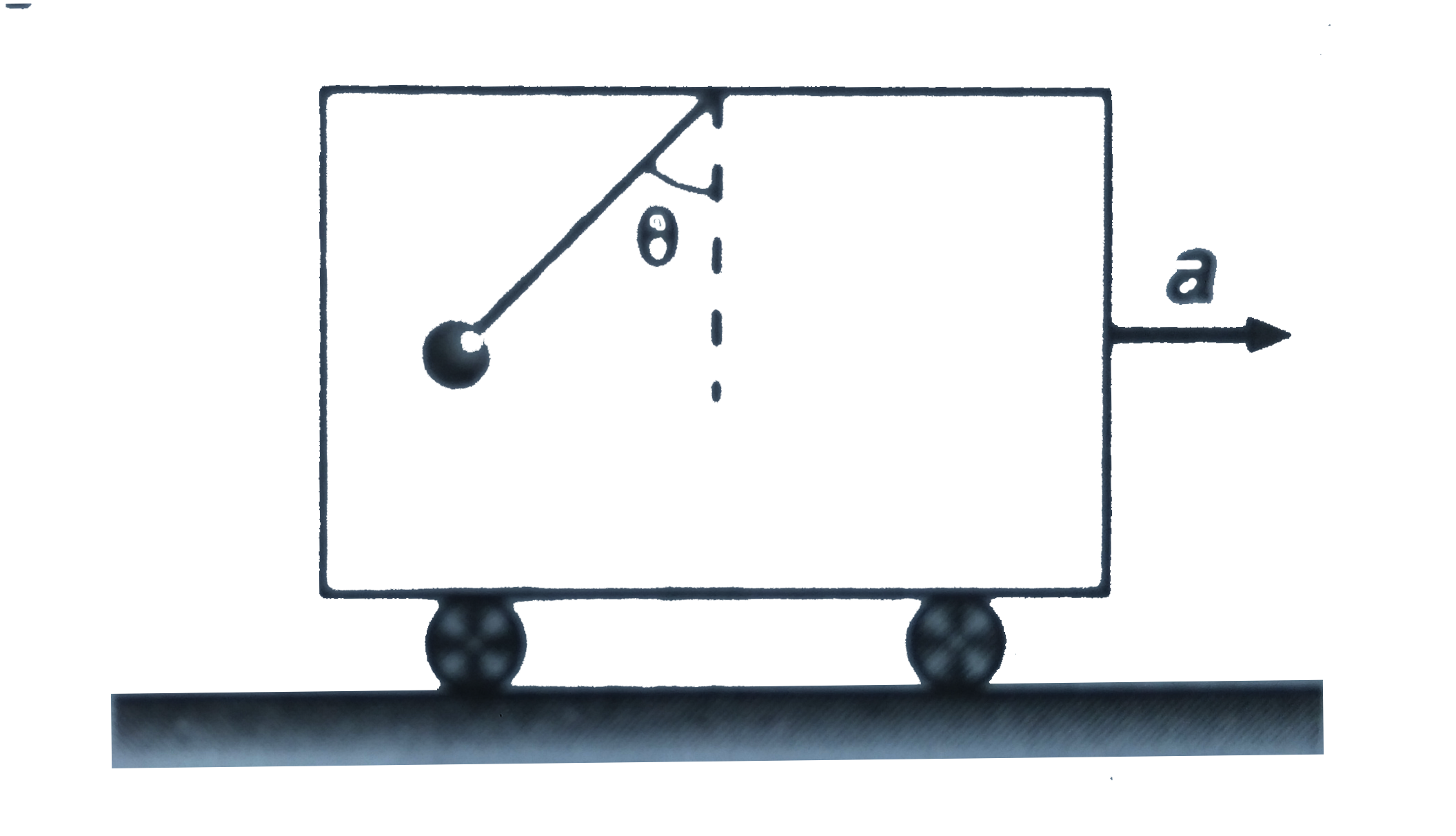
A small metallic sphere of mass m is suspended from the ceiling of a car accelerating on a horizontal road with constant acceleration a. The tension in the string attached with metallic sphere is

$m (g + a)$

$m (g - a)$

$m \sqrt{g^{2} + a^{2}}$

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem of finding the tension in the string attached to a small metallic sphere suspended in a car that is accelerating horizontally, we can follow these steps:
1. Identify the Forces Acting on the Sphere:
- The weight of the sphere acting downwards: $F_{g} = m g$ (where $m$ is the mass of the sphere and $g$ is the acceleration due to gravity).
- The tension in the string, $T$ , acting at an angle $θ$ with the vertical.
- A pseudo force acting on the sphere in the opposite direction of the car's acceleration, which is $F_{p s e u d o} = m a$ (where $a$ is the acceleration of the car).
2. Resolve the Tension into Components:
- The vertical component of the tension: $T cos θ$ (balances the weight of the sphere).
- The horizontal component of the tension: $T sin θ$ (balances the pseudo force).
3. Set Up the Equations:
- For vertical equilibrium (forces in the vertical direction must balance):
$T cos θ = m g (1)$
- For horizontal equilibrium (forces in the horizontal direction must balance):
$T sin θ = m a (2)$
4. Square Both Equations:
- Squaring equation (1):
$(T cos θ)^{2} = (m g)^{2} \Rightarrow T^{2} {cos}^{2} θ = m^{2} g^{2} (3)$
- Squaring equation (2):
$(T sin θ)^{2} = (m a)^{2} \Rightarrow T^{2} {sin}^{2} θ = m^{2} a^{2} (4)$
5. Add the Two Squared Equations:
- Adding equations (3) and (4):
$T^{2} {cos}^{2} θ + T^{2} {sin}^{2} θ = m^{2} g^{2} + m^{2} a^{2}$
- Factor out $T^{2}$ :
$T^{2} ({cos}^{2} θ + {sin}^{2} θ) = m^{2} (g^{2} + a^{2})$
- Since ${cos}^{2} θ + {sin}^{2} θ = 1$ :
$T^{2} = m^{2} (g^{2} + a^{2})$
6. Solve for Tension $T$ :
- Taking the square root of both sides:
$T = m \sqrt{g^{2} + a^{2}}$
Final Answer:
The tension in the string attached to the metallic sphere is:
$T = m \sqrt{g^{2} + a^{2}}$

Updated on:18/9/2024

A car accelerates on a horizontal road due to the force exerted by
Athe engine of the car
Bthe driver of the car
Cthe earth
Dthe road
A small sphere is suspended by a string from the ceiling of a car. If the car beings to move with a constant acceleration a, the inclination of the string to the vertical is:
A ${tan}^{- 1} (a / g)$ in the direction of motion
B ${tan}^{- 1} (a / g)$ opposite to the direction of motion
C ${tan}^{- 1} (g / a)$ in the direction of motion
D ${tan}^{- 1} (g / a)$ opposite to the direction of motion
A simple pendulum with a bob of mass m is suspended from the roof of a car moving with a horizontal acceleration a.
AThe string makes an angle of ${tan}^{- 1} (a / g)$ with the vertical
BThe string makes an angle of ${tan}^{- 1} (1 - \frac{a}{g})$ with the vertical
CThe tension in the string is $m \sqrt{a^{2} + g^{2}}$
DThe tension in the string is $m \sqrt{g^{2} - a^{2}}$