A police party is chasing a dacoit in a jeep which is moving at a constant speed v. The dacoit is on a motor cycle. When he is at a distance x from the jeep, he accelerates from rest at a constant rate α. Which of the following relations is true, if the police is able to catch the dacoit ?
v2<ax
v2<2ax
v2≥2ax
v2=ax
The correct Answer is:(c )
To solve the problem step by step, we need to analyze the motion of both the police jeep and the dacoit's motorcycle.
Step 1: Understanding the Motion of the Dacoit
The dacoit starts from rest and accelerates at a constant rate α. The distance he travels after time t can be described by the equation of motion:
sd=12αt2
where sd is the distance traveled by the dacoit.
Step 2: Understanding the Motion of the Police Jeep
The police jeep is moving at a constant speed v. The distance traveled by the police jeep in the same time t is given by:
sp=vt
where sp is the distance traveled by the police.
Step 3: Setting Up the Equation
At the moment the police catch the dacoit, the distance traveled by the dacoit plus the initial distance x should equal the distance traveled by the police jeep. Therefore, we can set up the equation:
sd+x=sp
Substituting the expressions for sd and sp, we have:
12αt2+x=vt
Step 4: Rearranging the Equation
Rearranging the equation gives us:
12αt2−vt+x=0
This is a quadratic equation in t.
Step 5: Applying the Condition for Real Roots
For the police to catch the dacoit, this quadratic equation must have real solutions for t. This means that the discriminant D of the quadratic equation must be greater than or equal to zero:
D=b2−4ac
In our case, a=12α, b=−v, and c=x. Thus, the discriminant becomes:
D=(−v)2−4(12α)x=v2−2αx
Setting the discriminant greater than or equal to zero gives:
v2−2αx≥0
Step 6: Final Relation
From the above inequality, we can conclude:
v2≥2αx
Conclusion
The relation that must hold true for the police to catch the dacoit is:
v2≥2αx
The dacoit starts from rest and accelerates at a constant rate α. The distance he travels after time t can be described by the equation of motion:
sd=12αt2
where sd is the distance traveled by the dacoit.
The police jeep is moving at a constant speed v. The distance traveled by the police jeep in the same time t is given by:
sp=vt
where sp is the distance traveled by the police.
At the moment the police catch the dacoit, the distance traveled by the dacoit plus the initial distance x should equal the distance traveled by the police jeep. Therefore, we can set up the equation:
sd+x=sp
Substituting the expressions for sd and sp, we have:
12αt2+x=vt
Rearranging the equation gives us:
12αt2−vt+x=0
This is a quadratic equation in t.
For the police to catch the dacoit, this quadratic equation must have real solutions for t. This means that the discriminant D of the quadratic equation must be greater than or equal to zero:
D=b2−4ac
In our case, a=12α, b=−v, and c=x. Thus, the discriminant becomes:
D=(−v)2−4(12α)x=v2−2αx
Setting the discriminant greater than or equal to zero gives:
v2−2αx≥0
From the above inequality, we can conclude:
v2≥2αx
The relation that must hold true for the police to catch the dacoit is:
v2≥2αx
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT EXEMPLAR PROBLEMS
6 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSERTION AND REASON
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - RELATIVE VELOCITY
18 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
A body moves from rest with a constant acceleration. Which one of the following graphs represents the variation of its kinetic energy K with the distance travelled x?
View SolutionA body moves from rest with a constant acceleration. Which one of the following graphs represents the variation of its kinetic energy K with the distance travelled x?
View Solution
Knowledge Check
In the figure below, a highway rest area (at D) and radar stations (at A and B) lie on a level east-west line, A is 9,000 feet due west of D. An airplane (at C) is shown directly above the rest area, flying due west at a constant speed of 300 feet per secod and at a constant altitude of 12,000 feet. The airplane is located at a straight-line distance of 15,000 feet from the radar station at A and 13,000 feet from the radar station at B.
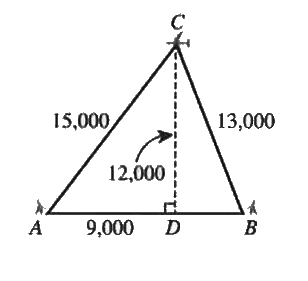
Which of the following values is closest to the number of seconds it will take for the airplane to fly from C to the point directly above the radar station at A?A17B30C40D43
A car accelerates from rest at constant rate for the first 10 s and covers a distance x. It covers a distance y in the next 10 s at the same acceleration. Which of the following is true?
View SolutionA car, starting from rest, has a constant acceleration for a time interval t1 during which it covers a distance In the next time interval the car has a constant retardation and comes to rest after covering a distance in time Which of the following relations is correct?
View SolutionThe velocity v of a particle moving along x - axis varies with ist position (x) as v=α√x, where α is a constant. Which of the following graph represents the variation of its acceleration (a) with time (t)?
View SolutionA police inspector in a jeepis chasing a pickpocket on a straightroad. The jeep is going at its maximum speed v (assumed uniform). The pickpocket rides on the motorcycle of a waiting friend when the jeepis at a distance of a waiting friend when the jeep is at a distance d away, and the motorcycle starts with a constant acceleration a. Show that the pickpocket will be caught it v≥√2ad.
View SolutionA thief is running away on a straitht road in a moving with a speed of 9ms−1. A policeman chases him on a motor cycle moving at a speed of 10ms−1. If the instananeous separation of the jeep from the motor cycle is 100m, how long will it take for the policeman to catch the thief ?.
View SolutionA person decided to walk on an escalator which is moving at constant rate (speed). When he moves at the rate 1 step/sec. then he reaches top in 20 steps. Next day he goes 2 steps/sec. and reaches top in 32 steps. If speed of escalator is n steps/sec. Find the value of n
View SolutionA man of height 'h' is walking away from a street lamp with a constant speed 'v'. The height of the street lamp is 3h. The rate at which the length of the man's shadow is increasing when he is at a distance 10 h from the base of the street lamp is
View Solution
