Question

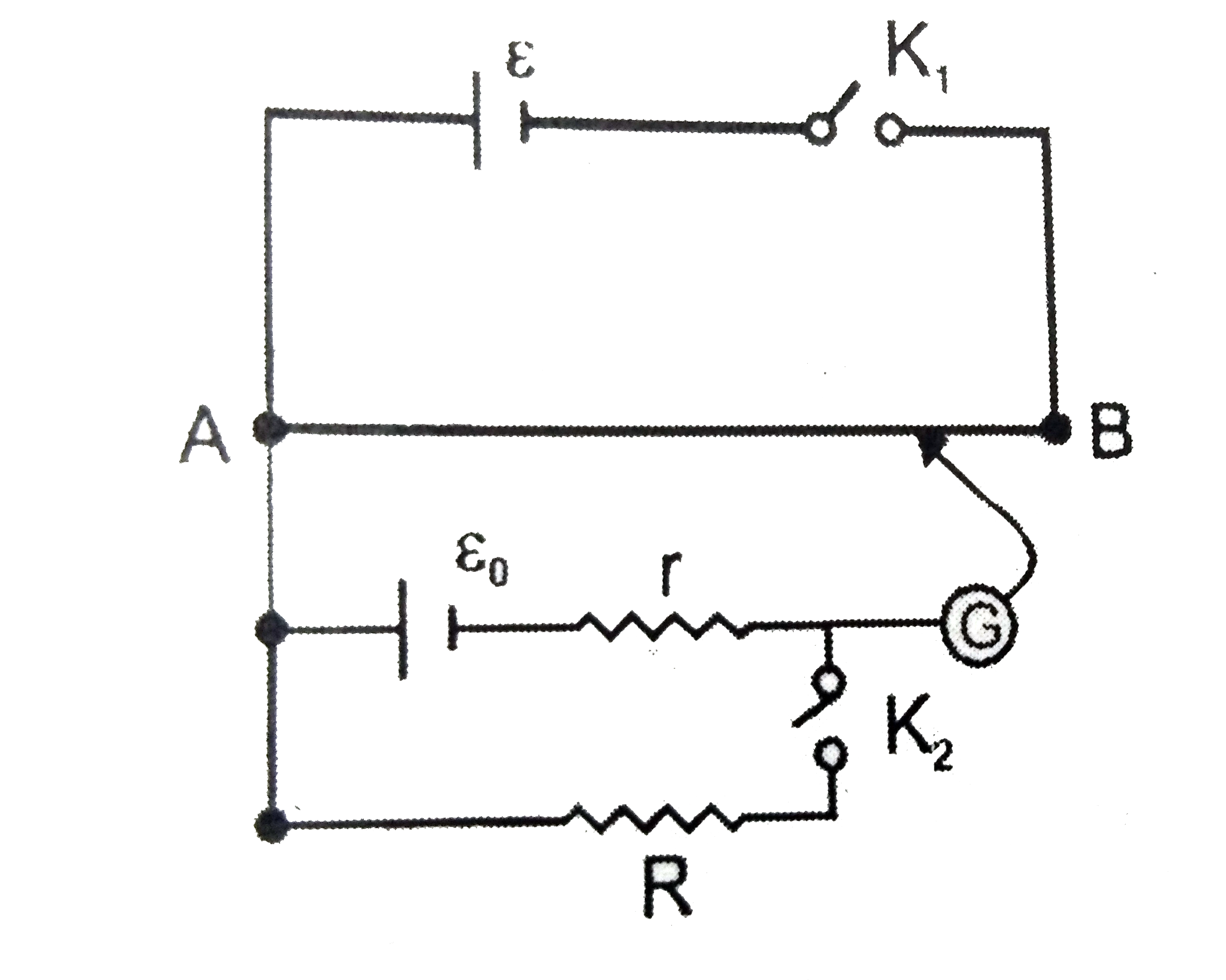
A potentiometer circuit has been setup for finding. The internal resistance of a given cell. The main battery used a negligible internal resistance. The potentiometer wire itself is $4m$ long. When the resistance, $R$, connected across the given cell, has value of
(i) Infinity $9.5\Omega$,
(ii) the 'balancing length' , on the potentiometer wire are found to be $3m$ and $2.85m$, respectively.
The value of internal resistance of the cell is

Options

A. `0.25 Omega`
B. `0.95 Omega`
C. `0.5 Omega`
D. `0.75 Omega`

Answer

C

Explanation

To find the internal resistance of the given cell using the potentiometer method, we can follow these steps:

Step 1: Understand the given data
- The potentiometer wire length is \(4 \, m\).
- When the resistance \(R\) is infinite, the balancing length \(L_1\) is \(3 \, m\).
- When the resistance \(R\) is \(9.5 \, \Omega\), the balancing length \(L_2\) is \(2.85 \, m\).
- The EMF of the cell and the main battery is \(2 \, V\) (as inferred from the context).

Step 2: Use the formula for internal resistance
The formula for internal resistance \(r\) of the cell is given by:

\( r = \left( \frac{L_1}{L_2} - 1 \right) R \)

Where:
- \(L_1\) is the balancing length when \(R\) is infinite.
- \(L_2\) is the balancing length when \(R\) is \(9.5 \, \Omega\).
- \(R\) is the external resistance connected across the cell.

Step 3: Substitute the values into the formula
Substituting the known values into the formula:

\( r = \left( \frac{3 \, m}{2.85 \, m} - 1 \right) \times 9.5 \, \Omega \)

Step 4: Calculate \( \frac{L_1}{L_2} \)
Calculating \( \frac{L_1}{L_2} \):

\( \frac{L_1}{L_2} = \frac{3}{2.85} \approx 1.0526 \)

Step 5: Calculate \( \frac{L_1}{L_2} - 1 \)
Now, calculate \( \frac{L_1}{L_2} - 1 \):

\( \frac{L_1}{L_2} - 1 \approx 1.0526 - 1 = 0.0526 \)

Step 6: Calculate the internal resistance \(r\)
Now, substitute this back into the equation for \(r\):

\( r = 0.0526 \times 9.5 \approx 0.5 \, \Omega \)

Final Answer
The internal resistance of the cell is approximately \(0.5 \, \Omega\).

---