The internal resistance of a cell is determined by using a potentiometer. In an experimetn, an external resistance of 60Ω is used across the given cell. When the key is closed, the balance length on the potentiometer decreases form 72 cm to 60 cm. calculate the internal resistance of the cell.
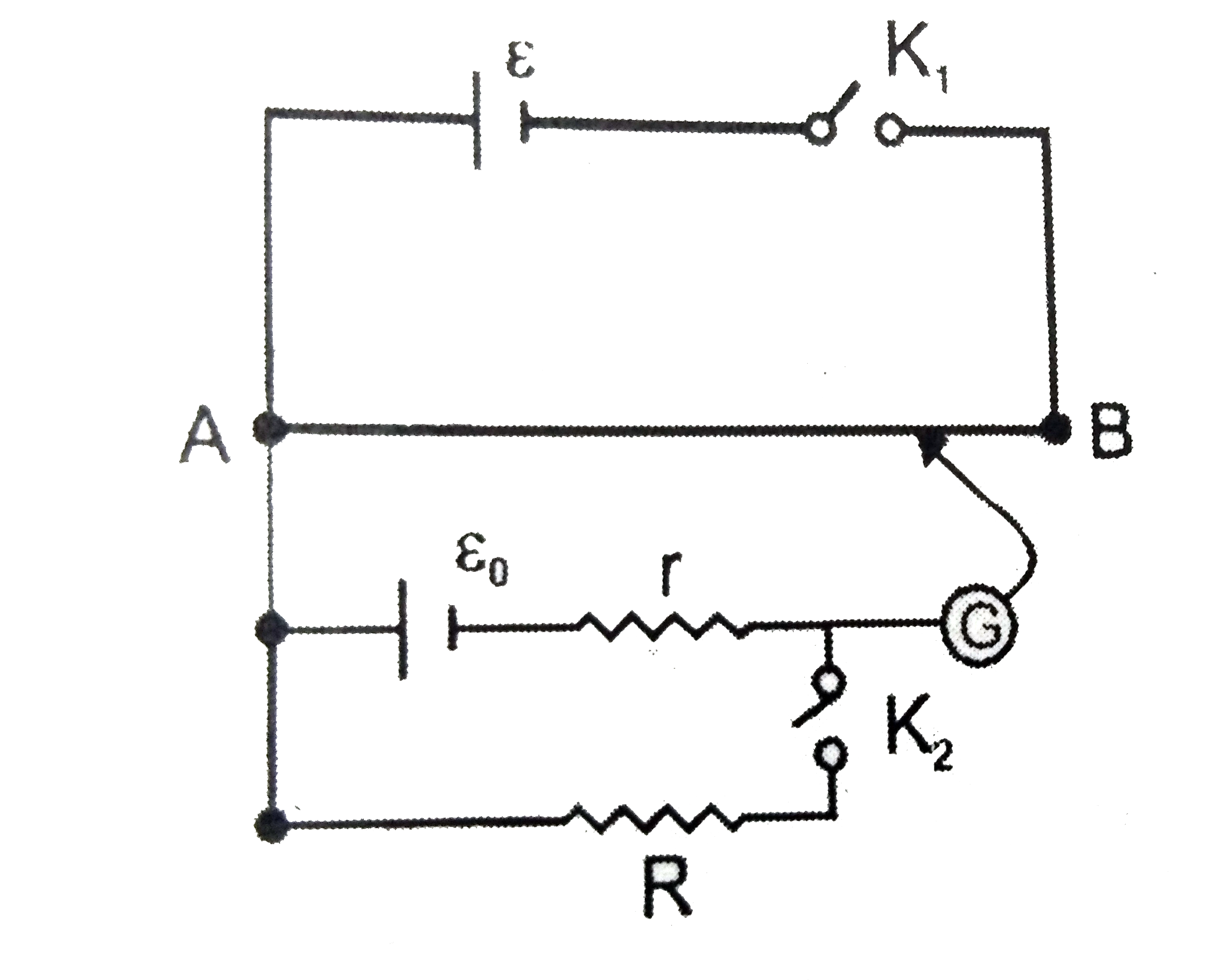
According to equation ε0=xl0…………(i)
V=IR=xl.....................(ii)
I=ε0R+r...............(iii)
From equation (i),(ii)and (iii) we get
r=R(l0l−1)
here l0=72cm,l=60cm,R=60Ω
∴r=(60)(7260−1)orr=12Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Solued miscellaneous Prolblems
8 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-1 (Part-1)
46 Videos
- COMMUNICATION SYSTEMSBOOK - RESONANCECHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 3
13 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP.No.71
1 Videos
Similar Questions
When a resistor of 5Ω is connected across a cell, its terminal potential differnce is balanced by 140 cm of potentiometer wire and when a resistance of 8Ω is connected across the cell, the terminal potential difference is balanced by 160 cm of the potentiometer wire. Find the internal resistance of the cell.
View SolutionWhen a resistance of 12 ohm is connected across a cell, its terminal potential difference is balanced by 120 cm length of potentiometer wire. When the resistance of 18 ohm is connected across the same cell, the balancing length is 150 cm. Find the balancing length when the cell is in open circuit. Also calculate the internal resistance of the cell.
View Solution
Knowledge Check
The internal resistance of a cell by potentiometer is given by
Ar1=R1(l1−l2l2)Br1=R1(E1−V1V1)Cboth 'a' and 'b'Dneither 'a' nor 'b'In an experiment to find the internal resistance of a cell by a potentiometer, a balance was obtained for 50 cm length of the potentiometer wire, with a cell of e.m.f. 2V. When the cell was shunted by a resistance of 2Ω, the balancing length of the potentiometer wire was 40 cm. What was the internal resistance of the cell ?
A0.25ΩB0.75ΩC0.5ΩD1Ω3V poteniometer used for the determination of internal resistance of a 2.4V cell. The balanced point of the cell in open circuit is 75.8cm. When a resistor of 10.2Ω is used in the external circuit of the cell the balance point shifts to 68.3cm length of the potentiometer wire. The internal resistance of the cell is
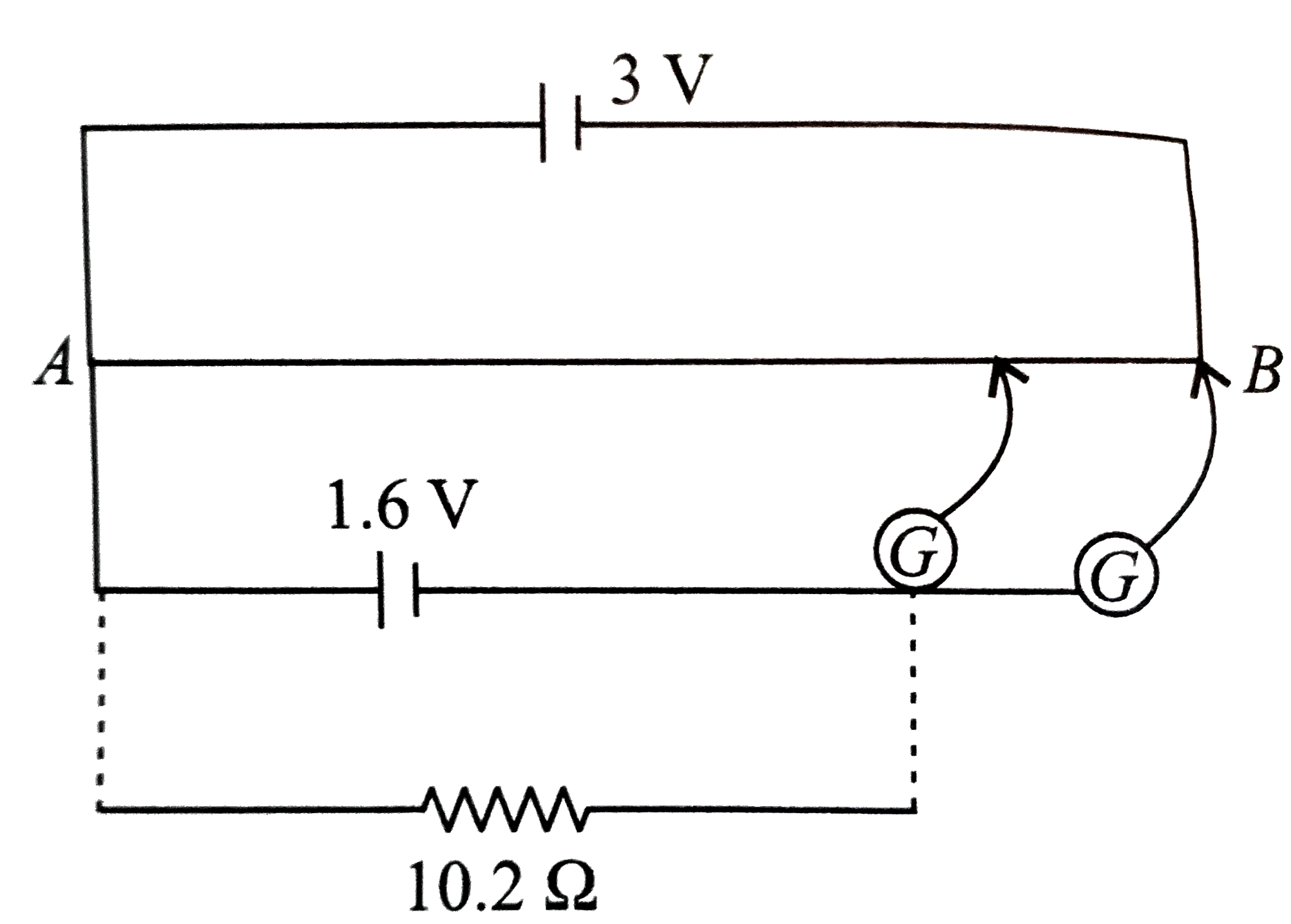 A2.5ΩB2.25ΩC1.12ΩD3.2Ω
A2.5ΩB2.25ΩC1.12ΩD3.2Ω
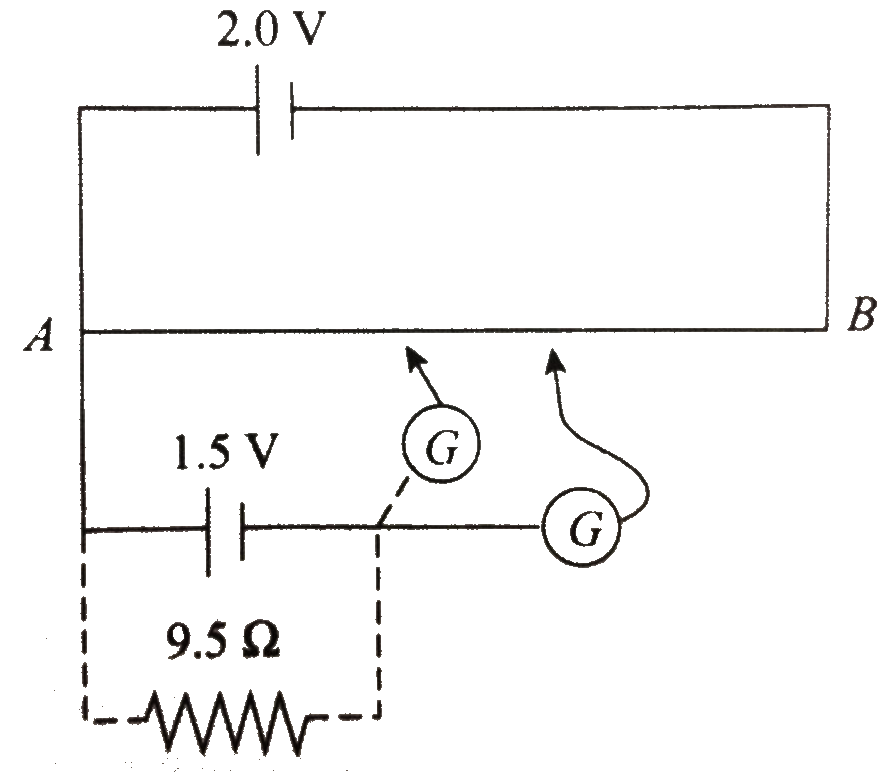
Fig. shows a 2.0 V potentiometer used for the determination of internal resistance of a 1.5 V cell. The balance point of the cell in open circuit is 76.3 cm. When a resistor of 9.5Ω is used in the external circuit of the cell, the balance point shifts to 64.8 cm length of the potentiometer wire. Determine the internal resistance of the cell.
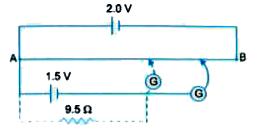
View SolutionFigure 6.13 shows a 2.0V potentiometer used for the determination of internal resistance of a 1.5V cell. The balance point of the cell in open circuit is 76.3cm. Whan a resistor of 9.5Ω is used in the external circuit of the cell, the balance point shifts to 64.8cm, length of the potentiometer. Dentermine the internal resistance of the cell.
View SolutionA potentiometer circuit with potentiometer wire 10 m long, and an ideal main battery of e.m.f 8 V, has been set up for finding the internal resistance of a given cell. When the resistance R, connected across the given cell, has values of (i) infinity, (ii) 10 omega , the balancing lengths, on the potentiometer wire are found to be 2.4 m and x respectively. If the internal resistance of the cell is 2 omega, the value of x is
View SolutionIn a potentiometer experiment , the balancing length for a cell was found to the 1.20 m . Now , a resistance of 10Ω is connected across the terminals of this cell and the balancing length becomes 80 cm . The internal resistance of this cell is .
View SolutionIn a potentiometer experiment , the balancing length for a cell was found to the 1.20 M . Now , a resistance of 10Ω is connected across the terminals of this cell and the balancing length becomes 80 cm . The internal resistance of this cell is .
View Solution
