A projectile is fired horizontally with a velocity u making an angle θ . Derive the expression for time of the flight . Solution in Tamil
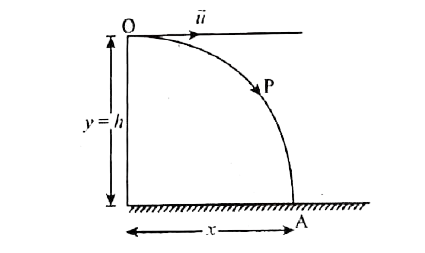
Let us consider a projectile, that is, thrown horizontal with an initial velocity →u from the top of a tower of height h in the figure .
Motion along horizontal direction : The particle has zero acceleration along x direction. So, the initial velocity u(x) remains constant throughout the motion. The distance traveled by the projectile at a time t is given by x=uxt+12at2
Since a = 0 along x direction, we get
x=uxt ...(1)
Motion along downward direction : Here uy=0 (initial velocity has no downward component), a = g .The distance y at time y is given by
y=uyt+12at2 , we get
y=12gt2 [u = 0, a = g] . . . (2)
Substituting the value of t from equation (1) in equation (2) we have
y=12gx2u2x=(g2u2x)x2
y=Kx2 ...(3)
Where K=g2u2x is a constant of proportionality .
Equation (3) gives the trajectory of the projectile. Thus , the path followed by the projectile is a parabola .
Horizontal range : The horizontal distance covered by the projectile from the foot of the tower to the point where the projectile hits the ground is called horizontal range. For horizontal motion, we have
sx=uxt+12at2
Here, sx=R (range), ux=u,a=0 (no horizontal acceleration) T is time of flight . Then horizontal range = u T.
Since the time of flight T =√2hg , we substitute this and we get the horizontal range of the particle as R=u√2hg .
Topper's Solved these Questions
- KINEMATICS BOOK - PREMIERS PUBLISHERSCHAPTER - KINEMATICS EXERCISE - Other important questions & answers (V. Numerical problems).
166 Videos
- KINEMATICS BOOK - PREMIERS PUBLISHERSCHAPTER - KINEMATICS EXERCISE - Other important questions & answers (III. Short answer questions).
26 Videos
- GRAVITATIONBOOK - PREMIERS PUBLISHERSCHAPTER - GRAVITATIONEXERCISE - OTHER IMPORTANT QUESTION & ANSWERS (CONCEPTUAL QUESTIONS)
34 Videos
- KINETIC THEORY OF GASESBOOK - PREMIERS PUBLISHERSCHAPTER - KINETIC THEORY OF GASESEXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS (VI. Conceptual Questions.)
8 Videos
Similar Questions
A crow is sitting on a branch of tree whose co-ordinates are (1,2,3) . A hunter is standing on the ground . Represent the position of the crow with respect to the hunter .
View SolutionWrite note on function with example.
View SolutionWhy a body weighs less at the equator than at the poles?
View SolutionWhen an automobile travels for a long distance , the air pressure in the tyres increases slightly . Why ?
View SolutionA projectile is fired with a velocity u at right angles to the slope, which is inclined at an angle θ with the horizontal. Derive an expression for the distance R to the point of impact.
 .
.
View SolutionA projectile is fired horizontally with a velocity u . Show that its trajectory is a parabola. Also obtain the expression for Time of flight .
View SolutionA projectile is fired horizontally with a velocity u making an angle θ . Derive the expression for time of the flight .
View SolutionA projectile is fired horizontally with a velocity u making an angle θ . Derive the expression for time of the flight .
View SolutionWhat is a projectile ? Obtain an expression for: maximum height , time of flight and the horizontal range when a projectile is fired at an angle theta with the horizontal.
View SolutionA projectile fired with velocity u at right angle to the slope which is inclined at an angle θ with horizontal. The expression for R is
View SolutionA projectile fired with velocity u at right angle to theslope which is inclined at an angle θ with horizontal. The expression for R is
View SolutionFor a projectile first with velocity u at an angle θ with the horizontal.

View SolutionA projectile is fired with a velocity 'u' making an angle theta with the horizontal. Show that its trajectory is a parabola.
View SolutionA projectile is projected with velocity u making angle θ with horizontal direction, find : time of flight.
View SolutionA projectile is fired at an angle θ with the horizontal with velocity u. Deduce the expression for the maximum height reached by it.
View SolutionA projectile fired with velocity u at right angle to the slope which is inclined at an angle theta with horizontal. The expression for R is
View Solution
