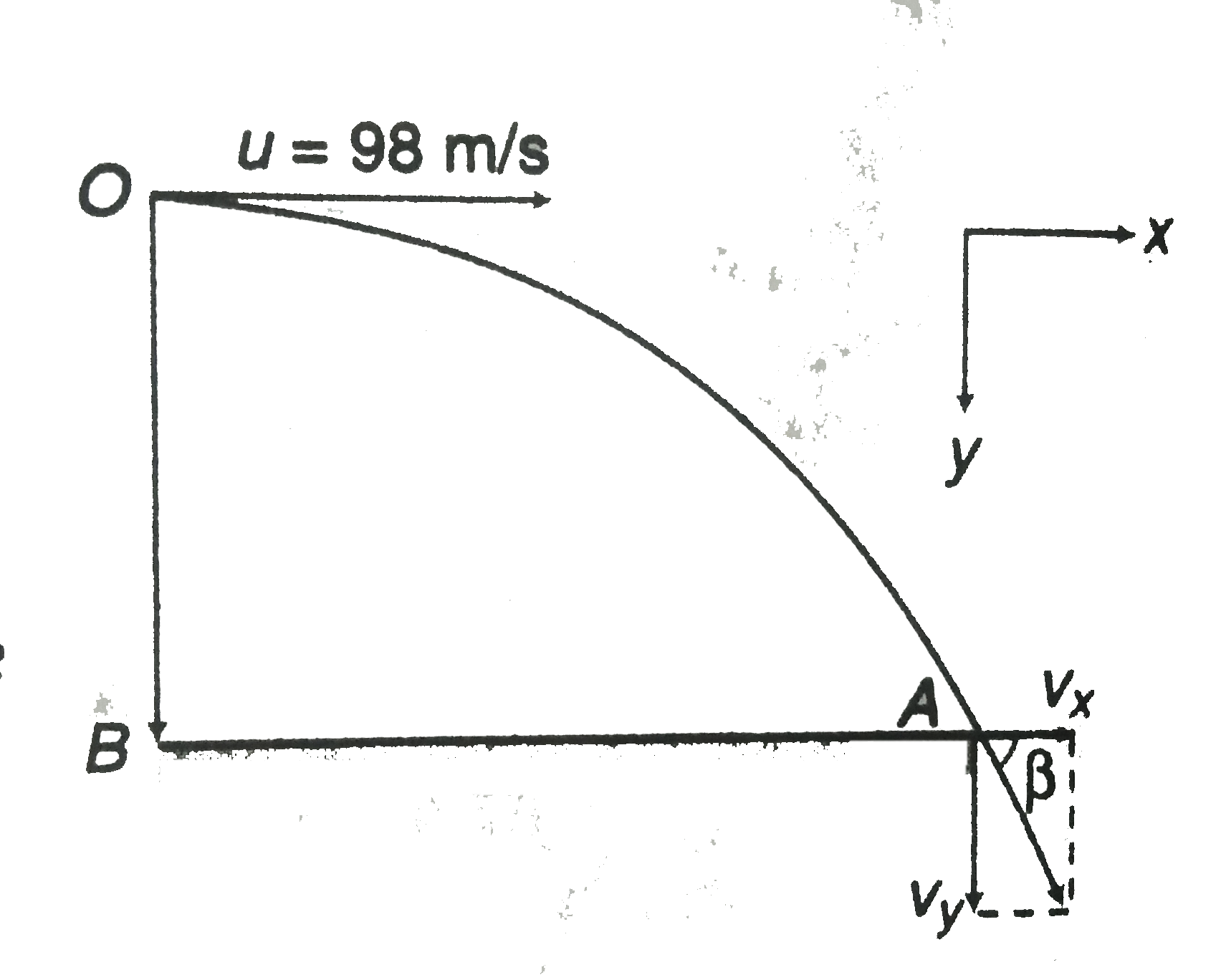
A projectile is fired horizontally with velocity of 98 m/s from the top of a hill 490 m high. Find
(a) the time taken by the projectile to reach the ground,
(b) the distance of the point where the particle hits the ground from foot of the hill and
(c) the velocity with which the projectile hits the ground. (g=9.8m/s2)
 .
.
12s , 980m , 98(√2)m/s β=45
10s , 98m , 98(√2)m/s β=45
10s , 980m , 98m/s β=45
10s , 980m , 98(√2)m/s β=45
The correct Answer is:D
Here, it will be more convenient to choose x and y
directions as shown in figure.
Here, ux=98ms,ax=0,uy=0anday=g
(a) At A, sy=490m. So, applying
sy=uyt+12(ay)t2
∴490=0+12(9.8)t2
∴t=10s
(b) BA=sx=uxt+12(ax)t2
or BA=(98)(10)+0
or BA=980m
(c) vx=ux+axt=98+0=98m/s
vy=uy+ayt=0+(9.8)(10)=98m/s
∴v=(√(v2x)+(v2y))=(√(98)2+(98)2)=98(√2)m/s
and tanβ=(vyvx)=9898=1
∴β=45∘
Thus, the projectile hits the ground with velocity 98(√2)m/s at an angle of β=45∘ with horizontal as shown in Fig. 7.9.
Topper's Solved these Questions
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Example Type 1
1 Videos
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Example Type 2
1 Videos
- MOTION IN A PLANEBOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
Similar Questions
A projectile is fired horizontally with a velocity of 98ms−1 from the top of a hill 490 m high. Find (i) the time taken to reach the ground (ii) the distance of the target from the hill and (iii) the velocity with which the projectile hits the ground.
View SolutionA particle is fired horizontally with a velocity of 100ms−1 for the top of a hill 400m high. Find (i) the time taken to reach the ground (ii) thedistance of the target from the hill and (iii) the velocity with which the projectile hits the ground. Take g=10ms−2.
View Solution
Knowledge Check
A projectile is fired horizontally from a tower which is 25 ft high from the level of the ground and reaches the ground at a horizontal distance of 1000 ft. The initial velocity is
A200ft/secB400ft/secC600ft/secD800ft/sec
From the top of a hill 480 m high , a projectile is fired horizontally with a speed of 96m/s . Calculate
(i) the time taken by projectile to reach the ground .
(ii) the distance of the target from the hill .
(iii) the velocity with which the projectile hits the ground . Take g=10ms−2
View SolutionA body is released from the top of a tower of height 50 m. Find the velocity with which the body hits the ground. (g=9.8m/s2)
View SolutionA body is relased from the top of a building of height 19.6 m. Find the velocity with which the body hits the ground .
View SolutionA body is relased from the top of a building of height 19.6 m. Find the velocity with which the body hits the ground .
View SolutionA ball is thrown horizontally from a point 100m above the ground with a speed of 20m/s. Find (a) the time it takes to reach the ground, (b) the horizontal distance it travels before reaching the ground, (c) the velocity (direction and magnitude) with which it strikes the ground.
View SolutionA body is projected downwards at an angle of 30∘ to the horizontal with a velocity of 9.8m/s from the top of a a tower 29.4m high. How long will it take before striking the ground ?
View SolutionA particle is thrown horizontally from a tower of height 20m. If the speed of projection is 20ms then the distance of point from the tower,where the particle hit the ground is:-
View Solution
