A projectile of mass 3m is projected from ground with velocity 20√2m/s at 45∘. At highest point it explodes into two pieces. One of mass 2m and the other of mass m. Both the pieces fly off horizontally in opposite directions. Mass 2m falls at a distance of 100m from point of projection. Find the distance of second mass from point of projection where it strikes the ground.
(g=10m/s2)
The correct Answer is:C, D
To solve the problem step by step, we will analyze the motion of the projectile, the explosion, and the subsequent motion of the two pieces.
Step 1: Calculate the Range of the Projectile
The range R of a projectile is given by the formula:
R=u2sin(2θ)g
where:
- u=20√2m/s (initial velocity)
- θ=45∘ (angle of projection)
- g=10m/s2 (acceleration due to gravity)
Calculating R:
R=(20√2)2sin(90∘)10=80010=80m
Step 2: Analyze the Explosion
At the highest point of the projectile's trajectory, it explodes into two pieces:
- Mass 2m falls horizontally and lands 100m away from the point of projection.
- Mass m will fall in the opposite direction.
Step 3: Use the Center of Mass Concept
The center of mass of the system before and after the explosion remains unchanged. The position of the center of mass xcm can be calculated using:
xcm=m1x1+m2x2m1+m2
where:
- m1=m (mass of the second piece)
- x1 = distance where mass m lands (unknown)
- m2=2m (mass of the first piece)
- x2=100m (distance where mass 2m lands)
Since the total mass is 3m and the center of mass position before the explosion is 80m:
80=m⋅x1+2m⋅1003m
Step 4: Simplify the Equation
Multiplying through by 3m to eliminate the denominator:
240m=m⋅x1+200m
Dividing through by m (assuming m≠0):
240=x1+200
Step 5: Solve for x1
Rearranging the equation gives:
x1=240−200=40m
Conclusion
The distance of the second mass m from the point of projection where it strikes the ground is 40m.
The range R of a projectile is given by the formula:
R=u2sin(2θ)g
where:
- u=20√2m/s (initial velocity)
- θ=45∘ (angle of projection)
- g=10m/s2 (acceleration due to gravity)
R=(20√2)2sin(90∘)10=80010=80m
At the highest point of the projectile's trajectory, it explodes into two pieces:
- Mass 2m falls horizontally and lands 100m away from the point of projection.
- Mass m will fall in the opposite direction.
The center of mass of the system before and after the explosion remains unchanged. The position of the center of mass xcm can be calculated using:
xcm=m1x1+m2x2m1+m2
where:
- m1=m (mass of the second piece)
- x1 = distance where mass m lands (unknown)
- m2=2m (mass of the first piece)
- x2=100m (distance where mass 2m lands)
80=m⋅x1+2m⋅1003m
Multiplying through by 3m to eliminate the denominator:
240m=m⋅x1+200m
Dividing through by m (assuming m≠0):
240=x1+200
Rearranging the equation gives:
x1=240−200=40m
The distance of the second mass m from the point of projection where it strikes the ground is 40m.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Type 11videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Solved Examples13videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions15videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery19videos
CIRCULAR MOTION
Similar Questions
A particle is projected from ground with velocity 40√2m/s at 45∘. At time t=2s
View SolutionA particle is projected from ground with velocity 20(√2)m/s at 45∘. At what time particle is at height 15 m from ground? (g=10m/s2)
View SolutionA particle is projected from a tower as shown in figure, then find the distance from the foot of the tower where it will strike the ground. (g=10m/s2)
 View Solution
View SolutionA particle is projected from ground with velocity 3ˆi+4ˆj m/s. Find range of the projectile :-
View SolutionA particle is projected from ground with velocity 40(√2)m/s at 45∘. Find
(a) velocity and
(b) displacement of the particle after 2 s. (g=10m/s2)View SolutionThe particle of mass 1 kg is projected with velocity 20√2m/s at 45∘ with ground . When , the particle is at highest point (g=10m/s2),
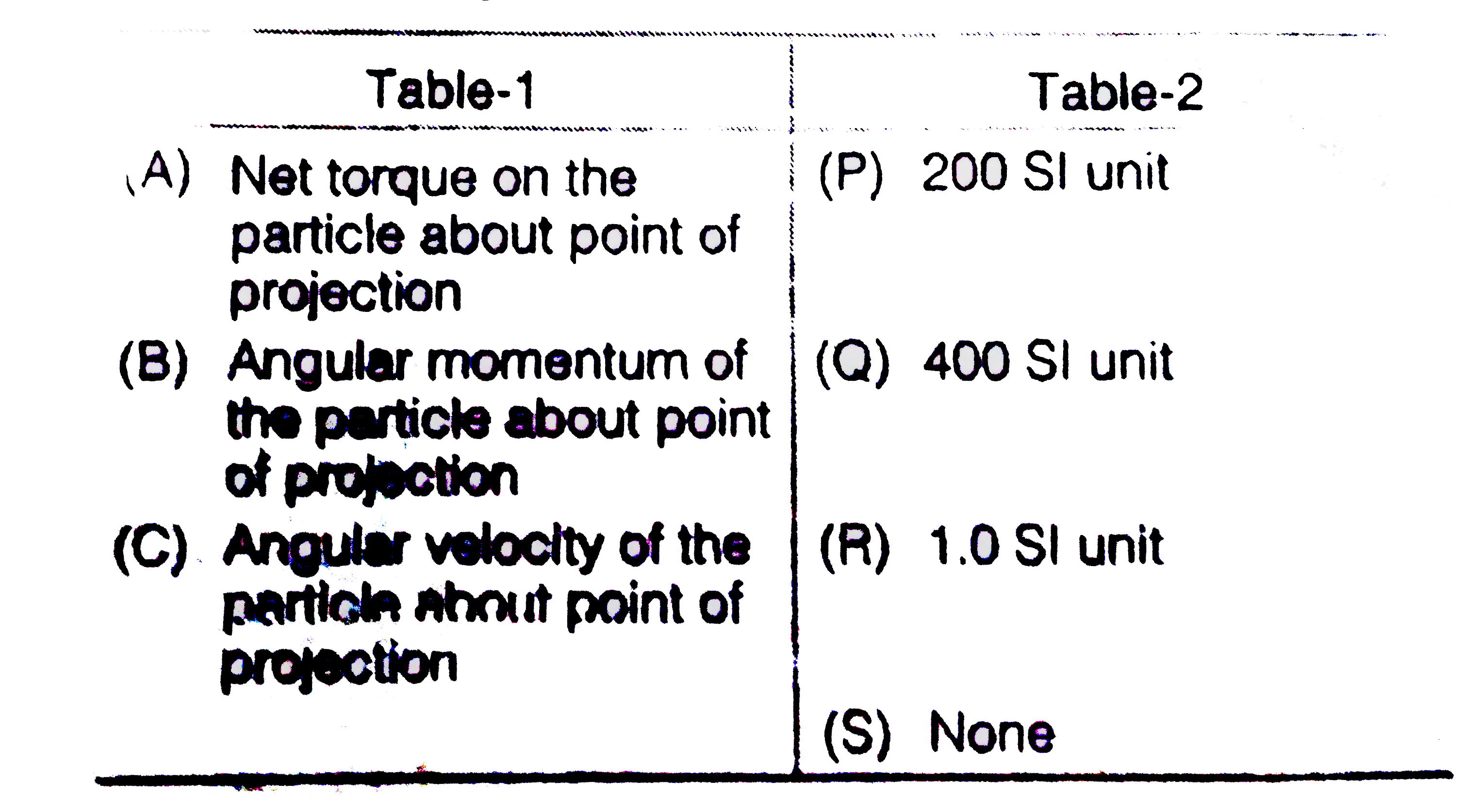 View Solution
View SolutionA particle of mass 4m is projected from the ground at some angle with horizontal. Its horizontal range is R. At the highest point of its path it breaks into two pieces of masses m and 3m, respectively, such that the smaller mass comes to rest. The larger mass finally falls at a distance x from the point of projection, where x is equal to
View SolutionA ball is projected from a point O as shown in figure it will strike the ground after (g = 10 m/s2 )
 View Solution
View SolutionA particle of mass m is projected form ground with velocity u making angle θ with the vertical. The de Broglie wavelength of the particle at the highest point is
View SolutionA body of mass m is projected from ground for horizontal range R. At the highest point it is fragmented into two identical parts. If one parts returns back to the point of projection, then other part will have the horizontal range
View Solution
