A projectile takes off with an initial velocity of 10m/s at an angle of elevation of 45∘. It is just able to clear two hurdles of height 2 m each, separated from each other by a distance d. Calculate d. At what distance from the point of projection is the first hurdle placed? Take g=10m/s2.
The correct Answer is:B, D
To solve the problem, we will follow these steps:
Step 1: Understand the projectile motion equations
The height y of a projectile at a horizontal distance x can be described by the equation:
y=xtanθ−gx22u2cos2θ
where:
- y is the height of the projectile,
- θ is the angle of projection,
- g is the acceleration due to gravity,
- u is the initial velocity,
- x is the horizontal distance from the point of projection.
Step 2: Substitute the known values
Given:
- u=10m/s
- θ=45∘
- g=10m/s2
- The height of the hurdles y=2m
Since tan45∘=1 and cos45∘=1√2, we can substitute these values into the equation:
2=x⋅1−10⋅x22⋅102⋅(1√2)2
Step 3: Simplify the equation
The equation simplifies to:
2=x−10x22⋅100⋅12=x−x210
Rearranging gives:
x−x210−2=0
Multiplying through by 10 to eliminate the fraction:
10x−x2−20=0
Rearranging gives:
−x2+10x−20=0
or
x2−10x+20=0
Step 4: Solve the quadratic equation
Using the quadratic formula x=−b±√b2−4ac2a:
Here, a=1,b=−10,c=20:
x=10±√(−10)2−4⋅1⋅202⋅1
x=10±√100−802
x=10±√202
x=10±2√52
x=5±√5
Step 5: Identify the distances
The two roots are:
- x1=5−√5 (distance to the first hurdle)
- x2=5+√5 (distance to the second hurdle)
Step 6: Calculate the distance d between the hurdles
The distance d between the two hurdles is:
d=x2−x1=(5+√5)−(5−√5)=2√5
Final Answers
- The distance from the point of projection to the first hurdle is 5−√5m.
- The distance d between the two hurdles is 2√5m.
The height y of a projectile at a horizontal distance x can be described by the equation:
y=xtanθ−gx22u2cos2θ
where:
- y is the height of the projectile,
- θ is the angle of projection,
- g is the acceleration due to gravity,
- u is the initial velocity,
- x is the horizontal distance from the point of projection.
Given:
- u=10m/s
- θ=45∘
- g=10m/s2
- The height of the hurdles y=2m
2=x⋅1−10⋅x22⋅102⋅(1√2)2
The equation simplifies to:
2=x−10x22⋅100⋅12=x−x210
Rearranging gives:
x−x210−2=0
Multiplying through by 10 to eliminate the fraction:
10x−x2−20=0
Rearranging gives:
−x2+10x−20=0
or
x2−10x+20=0
Using the quadratic formula x=−b±√b2−4ac2a:
Here, a=1,b=−10,c=20:
x=10±√(−10)2−4⋅1⋅202⋅1
x=10±√100−802
x=10±√202
x=10±2√52
x=5±√5
The two roots are:
- x1=5−√5 (distance to the first hurdle)
- x2=5+√5 (distance to the second hurdle)
The distance d between the two hurdles is:
d=x2−x1=(5+√5)−(5−√5)=2√5
- The distance from the point of projection to the first hurdle is 5−√5m.
- The distance d between the two hurdles is 2√5m.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 More Than One Correct8videos
PROJECTILE MOTION
- BOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery32videos
MOTION IN A PLANE
- BOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer8videos
PROPERTIES OF MATTER
Similar Questions
A ball projected with a velocity of 10m/s at angle of 30∘ with horizontal just clears two vertical poles each of height 1m. Find separation between the poles.
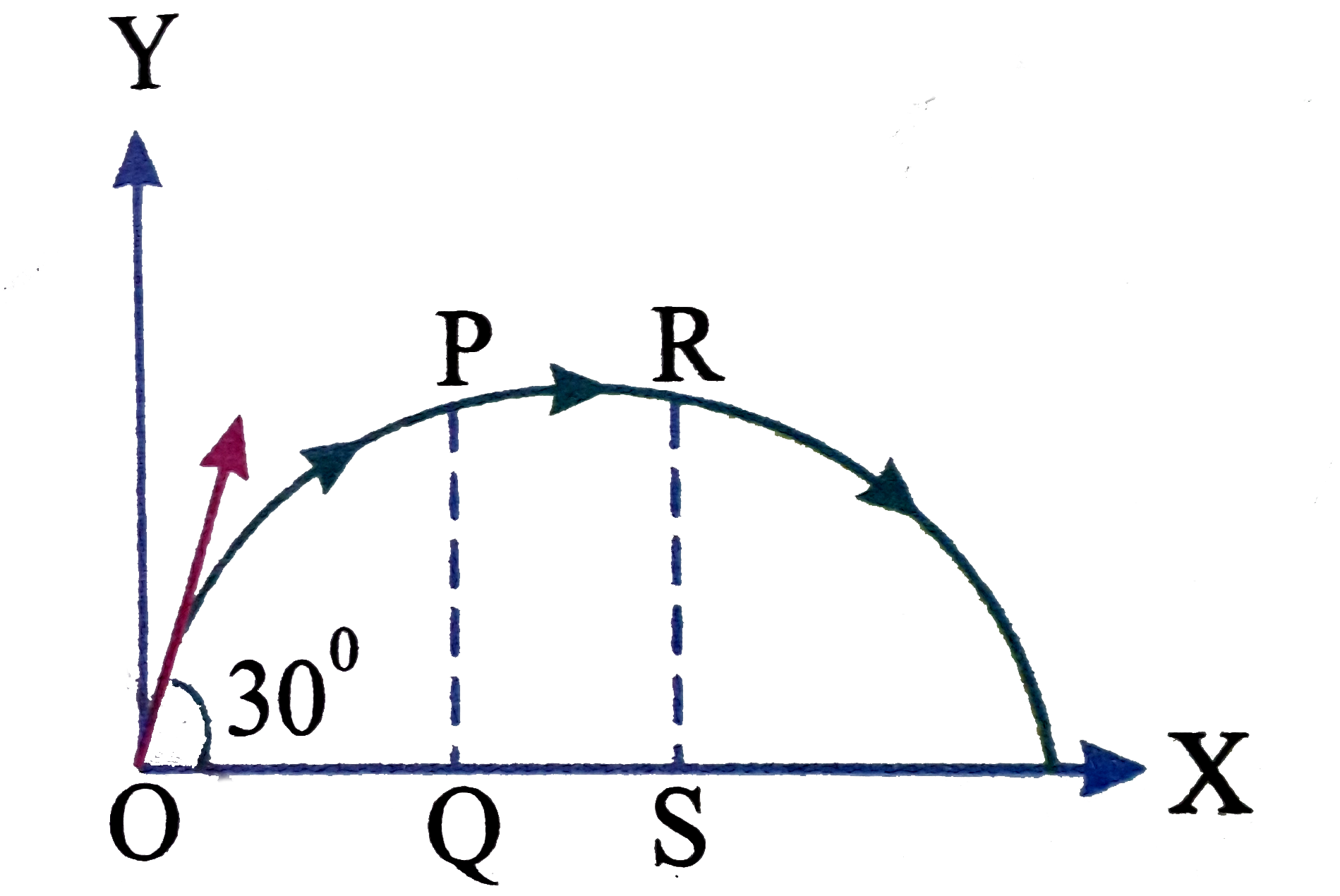 View Solution
View SolutionA particle is projected with a velocity 10 m//s at an angle 37∘ to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.
View Solution
Knowledge Check
- Question 1 - Select One
A projectile takes off with an initial velocity of 50m//s at an angle of 37∘ with horizontal, It is just able to clear two hurdles of height 25m each, separated from each other by a distance d Calculate d.
A160mB50mC320mD40m - Question 2 - Select One
An object is projected so that it just clears two walls of height 7.5 m and with separation 50m from each other. If the time of passing between the walls is 2.5s, the range of the projectile will be (g=10m/s2)
A35mB70mC140mD57.5m - Question 3 - Select One
A projectile is thrown with a velocity of 10√2m/s at an angle of 45∘ with horizontal. The interval between the moments when speed is √125m/s is (g=10m/s2)
A1.0sB1.5sC2.0sD0.5s
" A projectile is given an initial velocity "hat i+2hat j" .The cartesian equation of its path is "[" take "g=10m/s^(2)]
View SolutionA particle A is projected with an initial velocity of 60m/s at an angle 30∘ to the horizontal. At the same time a second particle B is projected in opposite direction with initial speed of 50m/s from a point at a distance of 100 m from A. If the particles collide in air, find (a)the angle of projection α of particle B, (b) time when the collision takes place and (c) the distance of P from A, where collision occurs. (g=10m/s2)
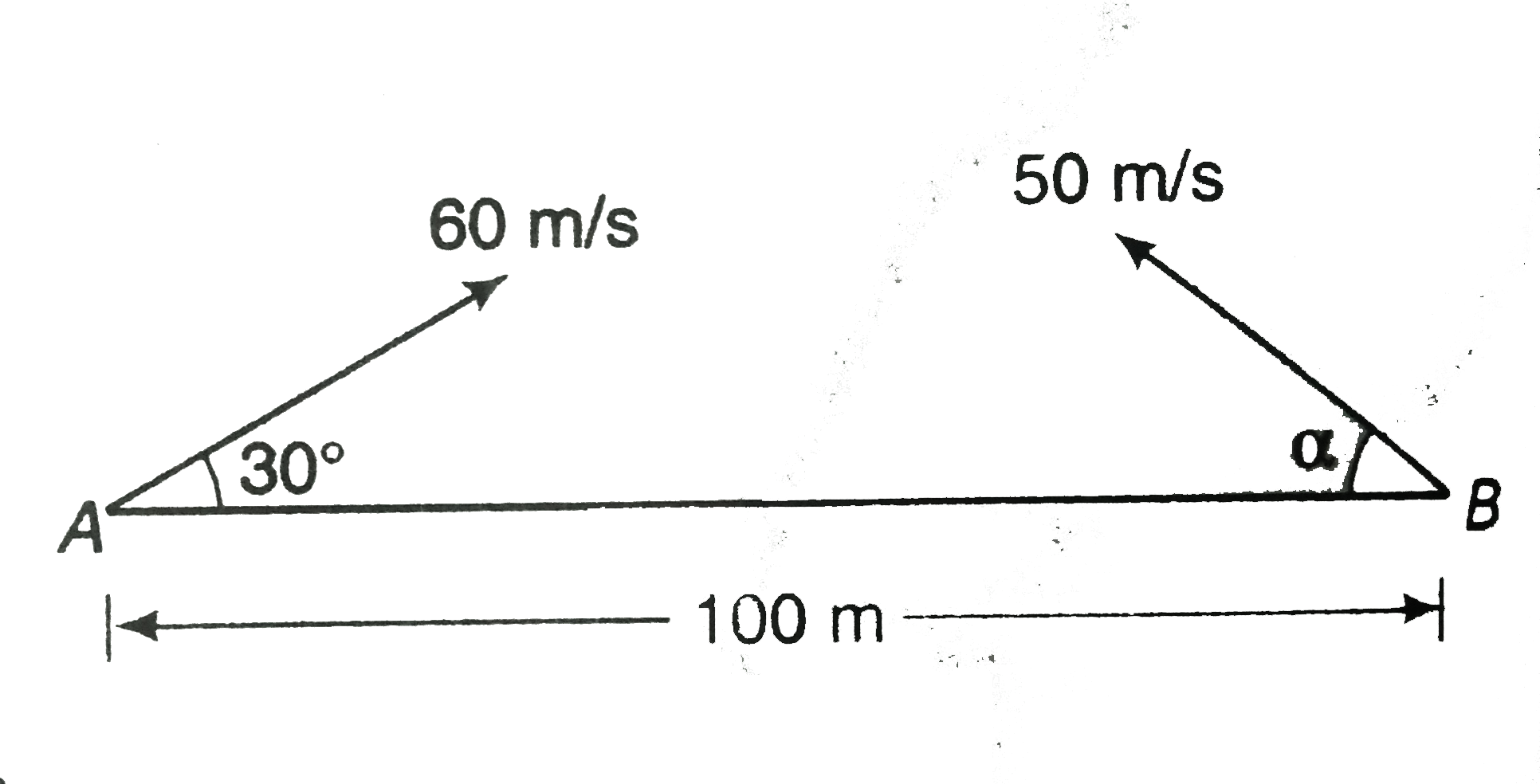 View Solution
View SolutionA stone is thrown from the top of a tower of height h=10m with speed v−10m/s. The distance of the landing point on the ground from the foot of the tower is R≤2√3k in meter. Calculate k. Take g=10m/s2
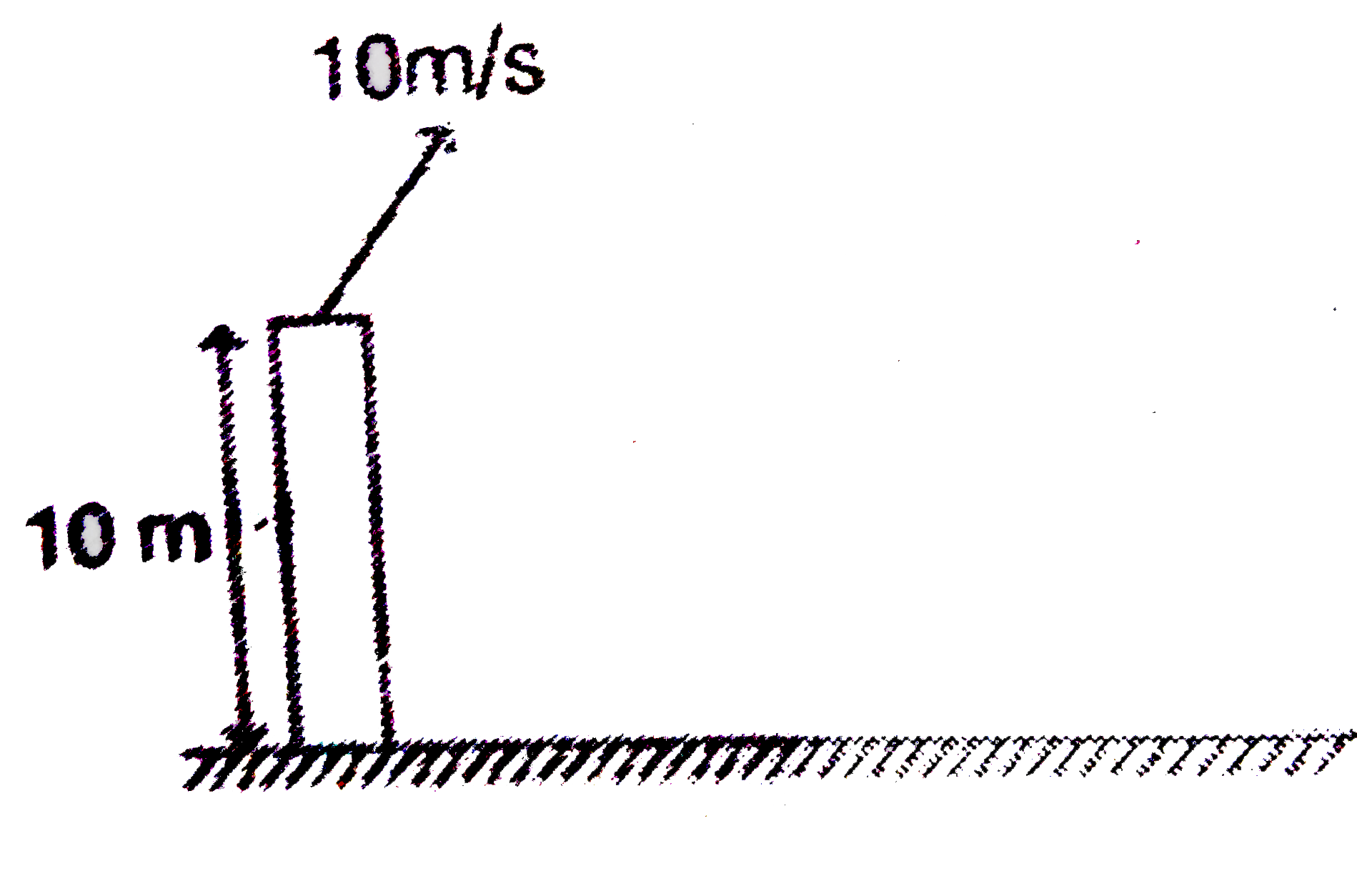 View Solution
View SolutionA projectile is projected with the initial velocity (6i+8j)m/s. The horizontal range is (g=10m/s2)
View SolutionA particle A is projected from the ground with an initial velocity of 10m/s at an angle of 60∘ with horizontal. From what height should an another particle B be projected horizontally with velocity 5m/s so that both the particles collide in ground at point C if both are projected simultaneously g=10m/s2.
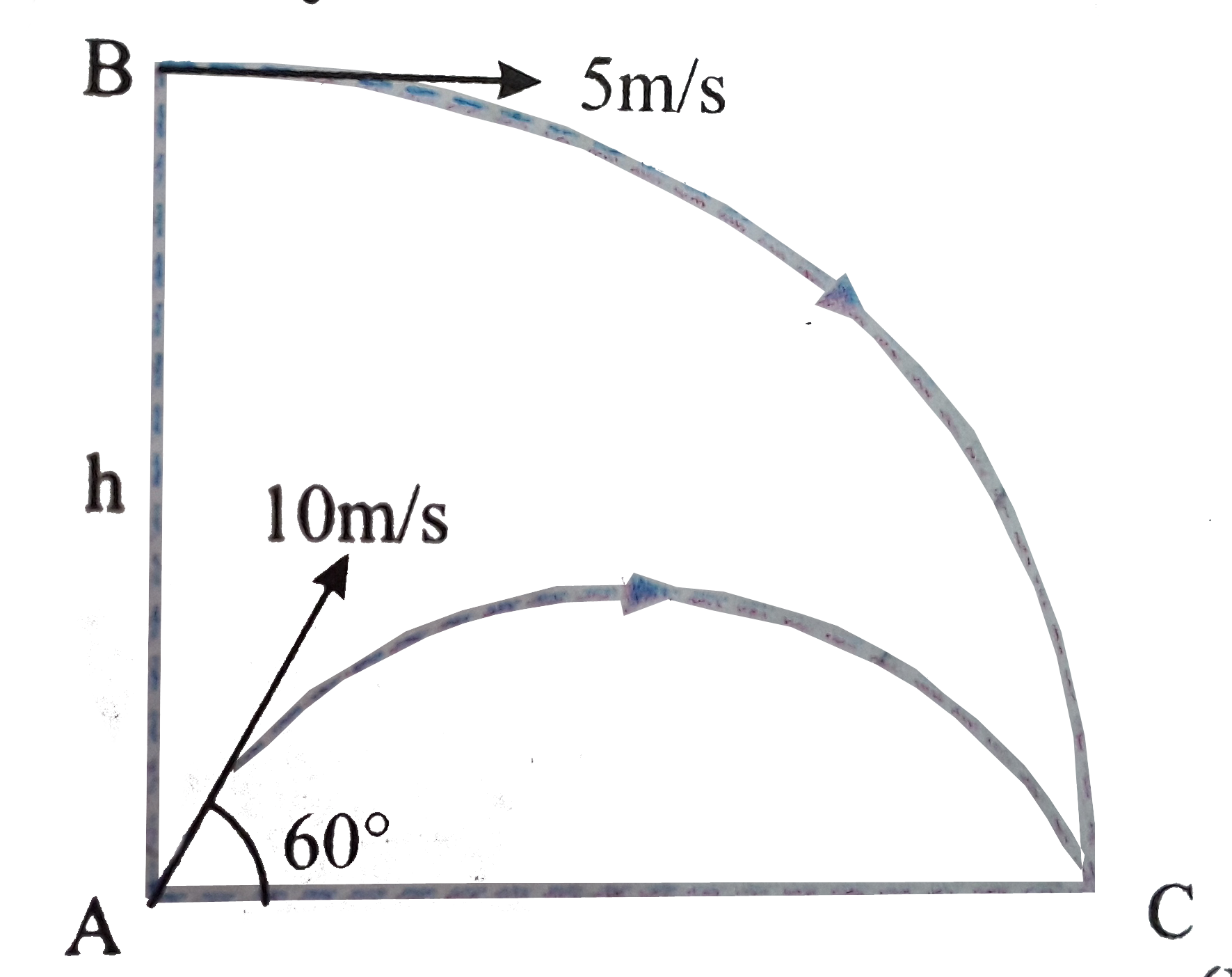 View Solution
View Solution

