A pulley of radius b=20cm is fixed with a shaft of radus a=10cm. Moment of inertia of shaft puley system is I=(33−800)kgm2 and the system is free to rotate about axis O of the shaft without friction.
A block B of mass m2=8kg is resting over ann ideal spring of force costant. K=2048Nm−1
Lower end of the spring is fixed to the floor and the spring is vertical. Thread connected betwen shaft and block B is just taut.

Another thead is connected between pulley and block A of mass m1=4kg. Initially this thread is loose. When block A is released first it falls freely through a height h=4051024m then the thread becomes taut and block B is jerked into motion.
calculate:
a. Initial compressiion of the spring
b. Velocity of block B when it is jerked into motion,
c. Loss of energy during that jerk (g=10ms−2)
Since initially thread connected with block A is loose, therefoe weight block B is balanced by compressive force in the spring.
ky0=mg⇒y0=mgK802048m
=y0=1.2532m or 12532cm
Since block A first fall freely through height h, therefore, it acquires a velocity v0=√2gh just before the thread becomes taut. Now the thread becomes taut and a impulse is developed in it. Due to htis impulse pulley is jerked into rotational motion and block B vertically upwards. Therfore wil not be impulse in spring as spring force is not an impulsive force. let impulses developed in threads connected with blocks A and B be J and J' respectively and let the pulley start to rotate clockwise with angular velocity ω0 then velocities of blocks A and B will be bω0 (downwards) and a ω0 (upwards) respectively.
Cosidering impulses and moment a as shown in the figure.

For block B,J'=m2aω0
m1v0−J=m1bω0
For block A,J.b−J'.a=Iω0
From i, ii and iii
J'=6.4Ns,J=4.8Ns
ω0=8rads−1
Kinetic ennergy of the system. just after the thread becomes taut,
E=12m1(bω0)2+12m2(aω0)2=+12ω20=9J
Loss of energy during the jerk E0−E=873128J
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples
12 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.1
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A carpet of mass M is rolled along its length so as to from a cylinder of radius R and is kept on a rough floor. When a negligibly small push is given to the cylindrical carpet, it stars rolling itself without sliding on the floor. Calculate horizontal velocity of cylindrical part of the carpet when its radius reduces to R/2.
View SolutionA uniform spherical shell of mass M and radius R rotates, about a vertical axis on frictionless bearing. A massless cord passes around the equator of the shell., over a pulley of rotational inertia I and radius r and is attached to small object of mass m that is otherwise free to fall under the influence of gravity. There is no friction of pulley's axle, the cord does not slip on the pulley. What is the speed of the object after it has fallen a distance h. from rest? Use work-energy considerations.

View SolutionA solid cylinder with r=0.1m and mass M=2kg is placed such that it is in contact with the vertical and a horizontal surface as shown in Fig. The coefficient of friction is μ=(1/3) for both the surfaces. Find the distance (in CM) from the centre of the cylinder at .which a force F=40N should be applied vertically so that the cylinder just starts rotating in anticlockwise direction.

View SolutionThe average power transmitted across a cross section by two sound waves moving in the same direction are equal. The wavelength of two sound waves are in the ratio of 1:2, then find the ratio of their pressure amplitudes.
View SolutionIn the system shown in the figure blocks A and B have mass m_(1)=2 kg and m_(2)=26//7 kg respectiely. Pulley having moment of inertia I=0.11kgm^(-2) can rotate without friction about a fixed axis. Inner and outer radii of pulley are a=10 cm and b=15 cm respectively. B is hanging with the thread wrapped around the pulley, while A lies on a rough inclined plane. Coefficient of friction being mu=sqrt(3)//10 Calculate as. Tension in each thread, and b. Acceleration of each block (g=10 ms^(-2))
View SolutionA stationary platform P which can rotate freely about a vertical axis (figure) supports a motor M and a balance weight N. The moment of inertia of the platform with the motor and the balance weight relative to this axis is equal to I. A light frame is fixed to the motor's shaft with a uniform sphere A rotating freely with an angular velocity omega_0 about a shaft BB^' coinciding with the axis OO^' . The moment of inertia of the sphere relative to the rotation axis is equal to I_0 . Find (a) the work performed by the motor in turning the shaft BB^' through 90^@ , through 180^@ , (b) the moment of external forces which maintains the axis of the arrangement in the vertical position after the motor turns the shaft BB^' through 90^@ .
View SolutionA uniform ring of mass M of outside radius r2 is fitted tightly with a shaft of radius r1. If the shaft is rotated with a constant angular acceleration. About it's axis, the moment of the elastic force in the ring about the axes of rotation is
View SolutionTwo blocks of mass 10 kg and 2 kg are connected by an ideal spring of spring constant K = 800 N//m and the system is placed on a horizontal surface as shown. The coefficient of friction between 10 kg block and surface is 0.5 but friction is absent between 2 kg and the surface. Initially blocks are at rest and spring is relaxed. The 2 kg block is displaced to elongate the spring by 1 cm and is then released. (a) Will 10 kg block move subsequently? (b) Draw a graph representing variation of magnitude of frictional force on 10 kg block with time. Time t is measured from that instant when 2 kg block is released to move.
View SolutionA spring of force constant K rests on a smooth floor, with one end fixed to a wall. A block of mass m hits the free end of the spring with velocity v. The maximum force exerted by the spring on the wall is
View SolutionA 10 kg collar P slides with negligible friction on the fixed vertical shaft. When the collar is released from rest at the bottom position shown, it moves up the shaft under the action of the constant force F = 200 N applied to the cable. The position of the small pulley at B is fixed. Find the spring constant k (in k−N/m) which the spring must have if its maximum compression is to be limited to 0.4 m.

View SolutionA Newtonian fluid fills the clearance between a shaft and a sleeve. When a force of 800 N is applied to the shaft, parallel to the sleeve, the shaft attains a speed of 2 cm s^(-1) . If a force of 2.4 kN is applied instead, the shaft would move with a speed of
View SolutionThe pulley as shown in the figure, consists of two discs of different diameters attached to the same shaft. The rope connected to the block of mass m_(1) = 1 kg passes over a smooth peg, while the block of mass m_(2) = 3 kg hangs vertically from one disc . The moment of inertia of the pulley is 0 . 2 kg m^(2), r_(1) = 5 cm and r_(2) = 10 cm . Find the tensions in the ropes and the accelerations of the blocks .
View SolutionIn a machine, a horizontal arm of 2 m is connected with a vertical shaft and is rotated at an angular velocity of 600 rpm in a horizontal plane. A 10 kg block is attached to the free end of the arm. Find out the force on the block and the force on the vertical shaft due to rotation of the block.
View SolutionThe period of the free oscillations of the system shown here if mass m1 is pulled down a little and force constant of the spring is k and masses of the fixed pulleys are negligible, is
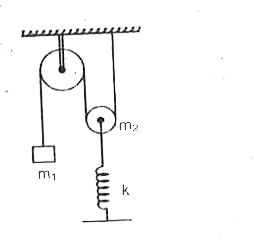
View SolutionA wheel is rotating with a speed of 500 rpm on a shaft. Second identical wheel, initially at rest is suddenly coupled on the same shaft. What is the speed of the resultant combination ? Assume that the moment of inertia of the shaft is negligible.
View SolutionA wheel is rotating with a speed of 500 rpm on a shaft. Second identical wheel, initially at rest is suddenly coupled on the same shaft. What is the speed of the resultant combination ? Assume that the moment of inertia of the shaft is negligible.
View Solution
