A pulley-rope-mass arrangement is shown in fig. Find the acceleration of block m1 when the masses are set free to move. Assume that the pulley and the ropes are ideal.
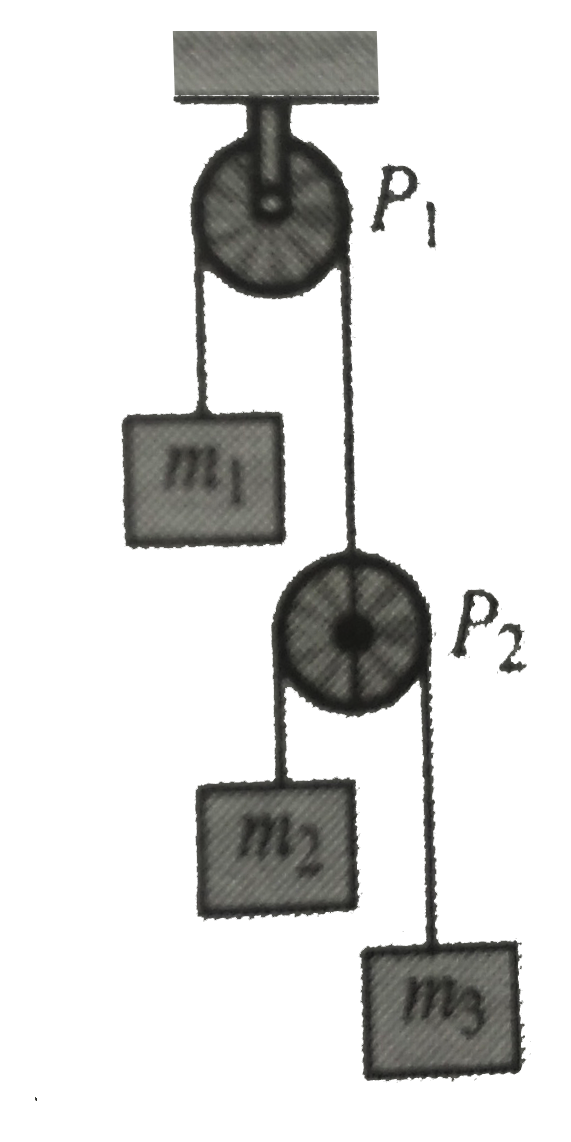
Constraint relations Method 1:
For the upper string, the length of string l1 not to change and for this string not to slacken, acceleration of m1 w.r.t. the fixed pulley = acceleration of the movable pulley w.r.t. the fixed pulley
or |a1|=|aP| ..(i)
Constraint relations for string 2
Let us assume that block m1 is moving down with acceleration a2 and a3 , respectively w.r.t. ground
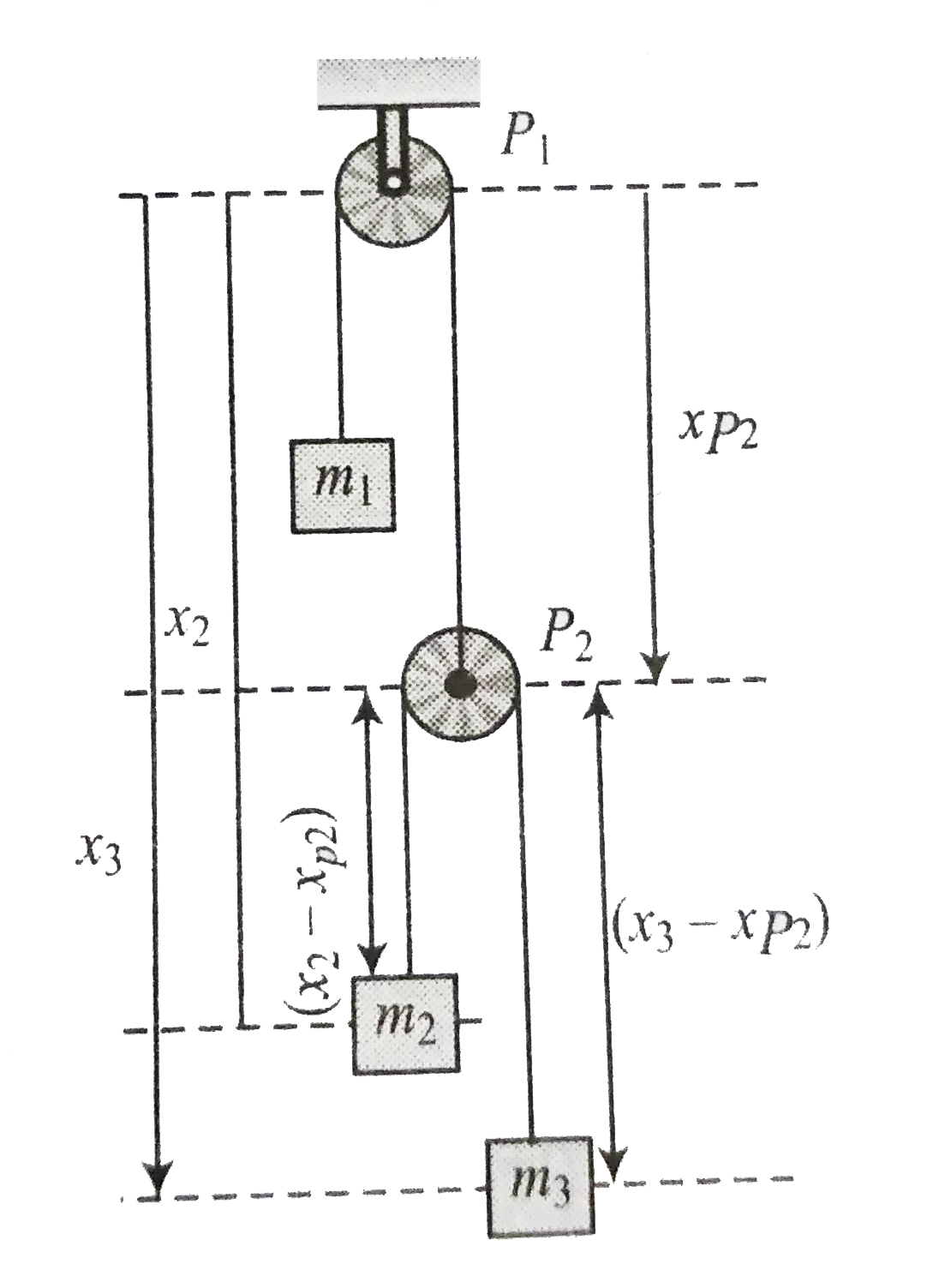
Total length of string 2 is constant. Therefore,
l2=(x2−xp2)+(x3−xp2)+l'0
where l0 is the length of string on pulley 2 passing through the pulley P2
l2=x2+x3−2xP2+l'0...(ii)
Differentiating Eq. (ii) w.r.t. time
dl2dt=0 (as total length of string is constanat)
dl'0d=0 (as length of string over pulley is constant)
differentiating eq.(ii) twice w.r.t. time
2a1=a3+a2 ..(iii)
Method 2: The acceleration of block m1 and pulley 2 will be same in magnitude. Now considering pulley 2 and block 2 and 3.
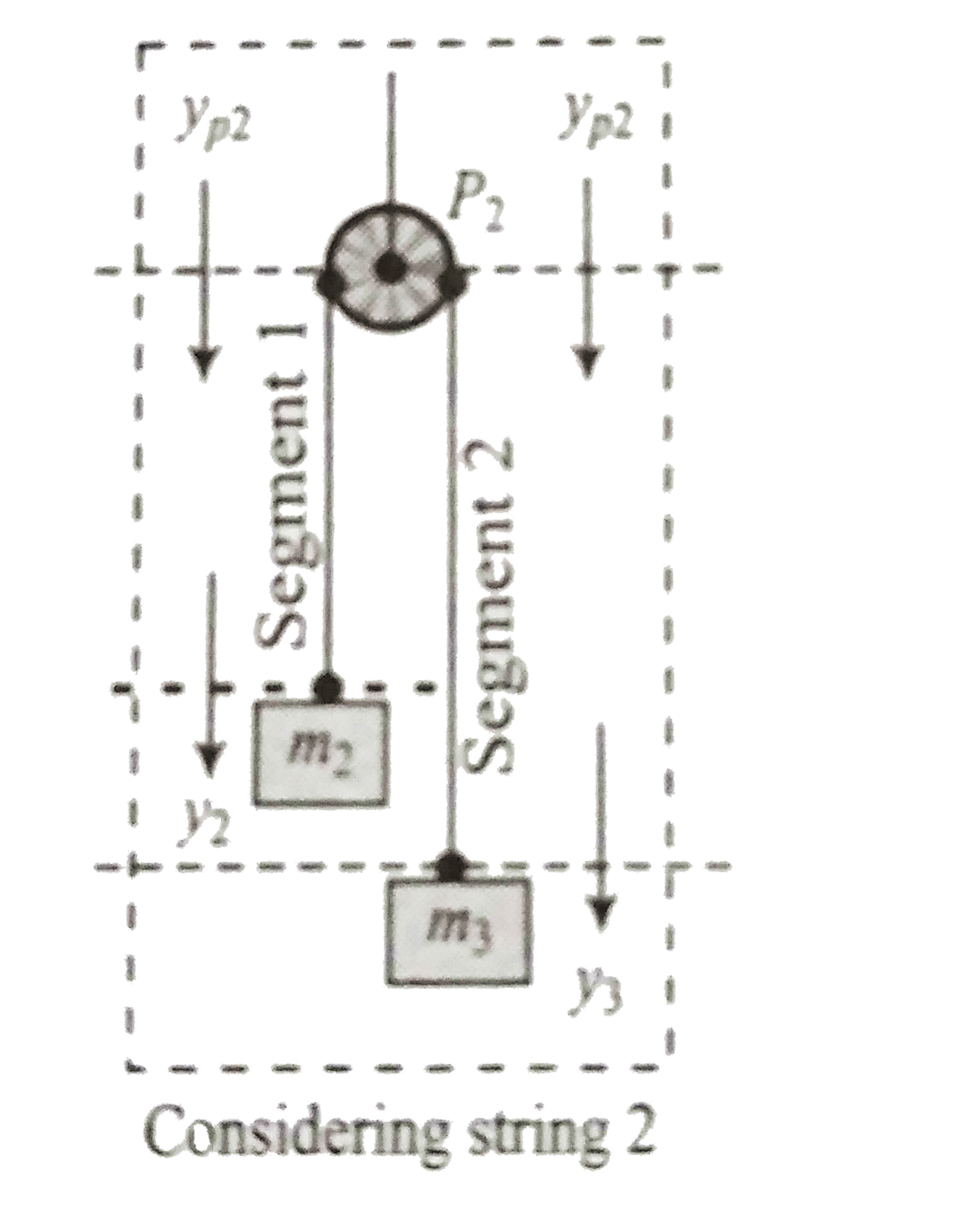
Change in the length of segment (1)
Δl1=(+y2)+(−yP2)=y2−yp2
Change in the length of segment (2)
Δl2=(y3)+(−yp2)=y3−yP2
Total sum of change in the segment length of string should be zero.
Δl=0=[y2−yP2]+[y2−yP2]
⇒Δl=0=y2+y3−2yP2
⇒2yp2=y3+y2⇒2ap2=a3+a2
or 2a1=a3+a2
This equation is same as (iii) calculate in method (2) .
Method 3: For the rope length l2 not to change and for this rope not to slacken acceleration of m2 w.r.t movable pully =-acceleration of m3w.r.t. movable pullwy
or (a2−ap)=−(a3−ap)
a2+a3−2ap=0⇒2a0=a2+a3
This equation is same as Eq.(iii) as calucutate in method 1 and 2
Applying Newton's laws of motion equations.
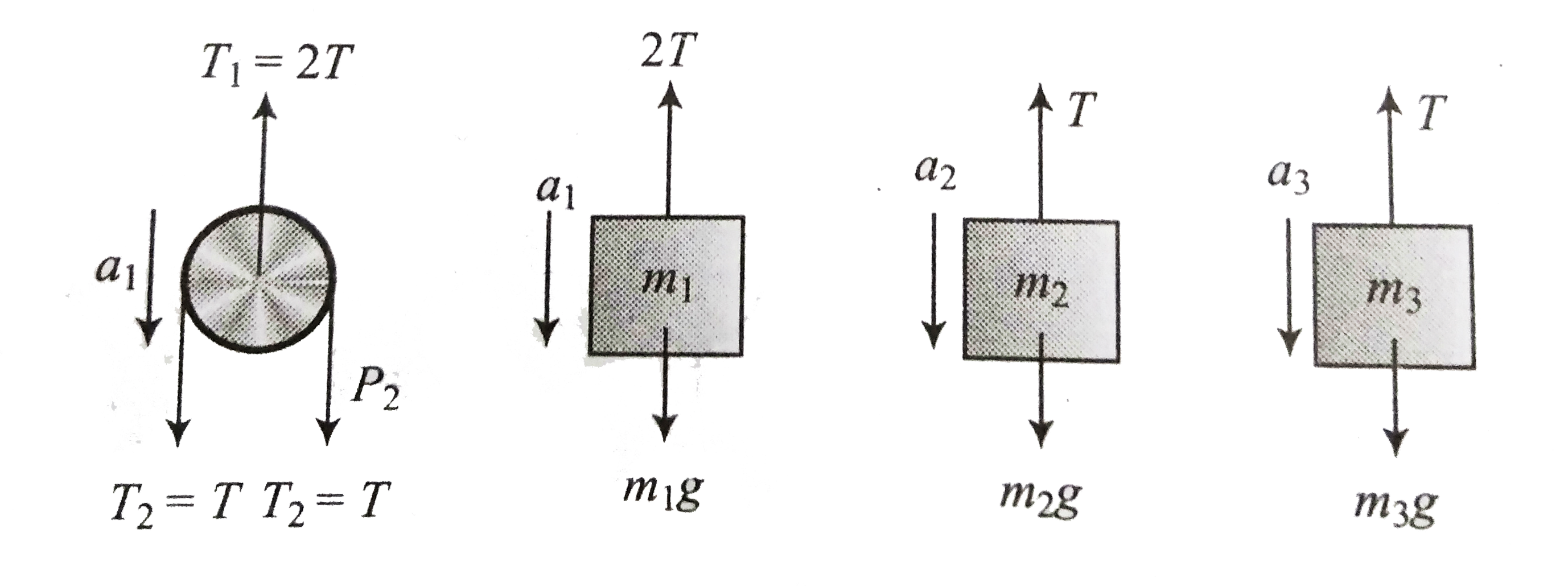
Free body diagram
Equation of motion
for m1:2T−m1g=m1a1 ...(iv)
for m2:m2g−T=m2a2...(v)
for m3:m3g−T=m3a3...(vi)
After solving (iii),(iv), (v), and (vi), we get
a1=4m2m3g−m1(m2+m3)g4m2m3+m1(m2+m3).
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.1
11 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
Find the acceleration blocks in fig. The pulley and the string are massless.

View SolutionConsider the arrangement shown in the figure. Find the acceleration of the block
(a) A monkey moves upward with respect to the rope with acceleration a0
(b) A monkey moves downward with respect to the rope with acceleration a0
Assume the surface smooth, pulley and string light.

View Solution
Knowledge Check
Find the acceleration of the block of mass m. Assume pulleys are massless and frictionless.
 Ag/3B2g3Cg2DNone
Ag/3B2g3Cg2DNoneIn the arrangement shown, the pulleys and the string are ideal. The acceleration of block B is.
 Ag/5Bg/2C2g/5D2g/3
Ag/5Bg/2C2g/5D2g/3In the arrangement shown, the mass m will ascend with an acceleration ( Pulley and rope are massless)
 AzeroBg5CgD2g
AzeroBg5CgD2g
Two monkeys A and B of equal mass 'm' can climb strings of a pulley arrangement as shown in figure.Find magnitude of acceleration in m/s^(2) of A with respect to rope so that the block remains stationary.It is given that B is just holding the string.Assume pulley is frictionless and string is massless and inextensible.
View SolutionThe velocities of A and B shown in fig. Find the speed (in ms−1) of block C. (Assume that the pulleys and string are ideal).

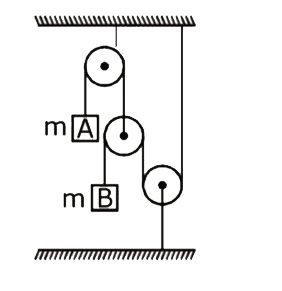
View SolutionIn the arrangement shown, the pulleys and the strings are ideal.The acceleration of the block B is
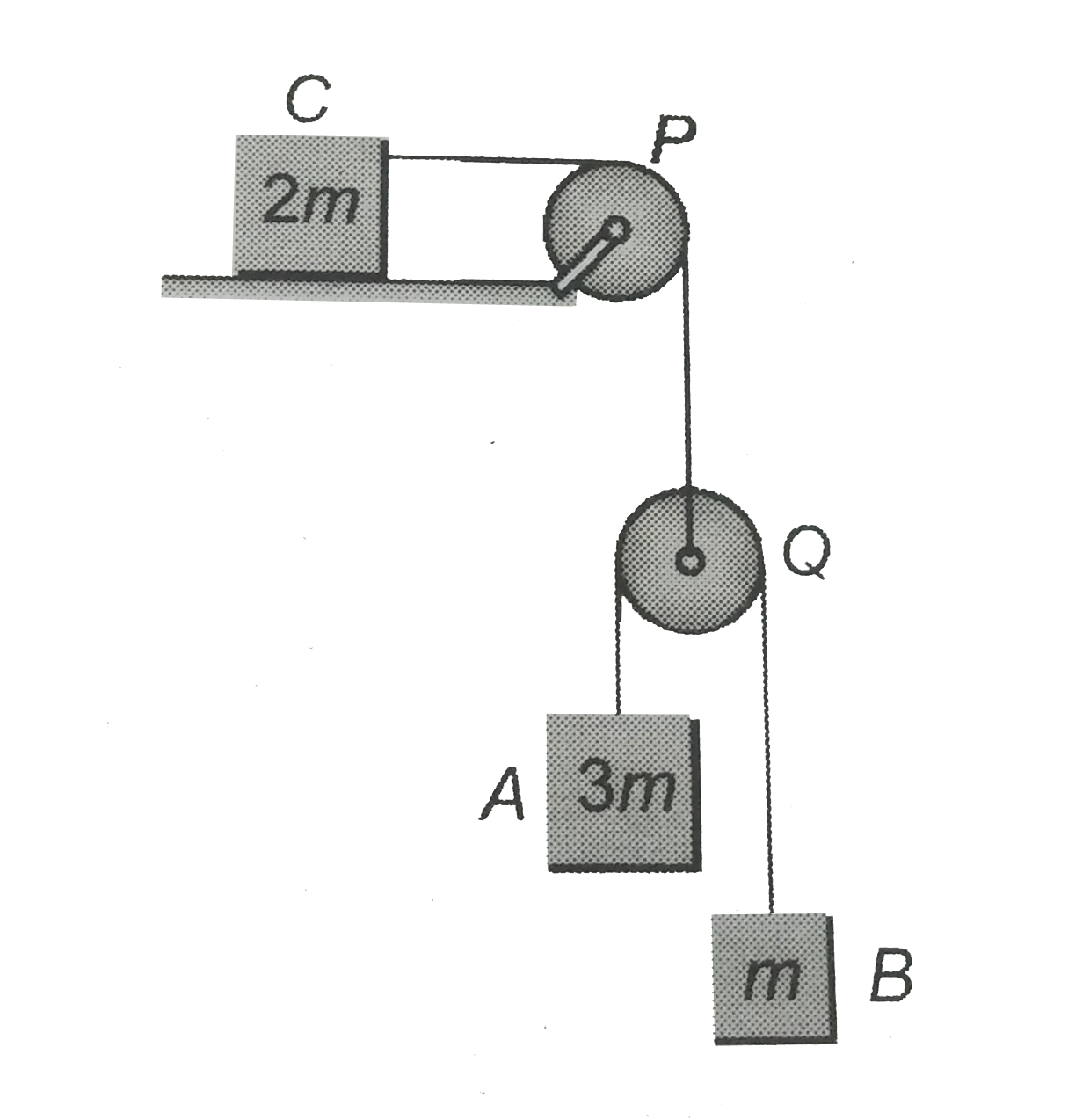
View SolutionIn the arrangement shown in the figure, the blocks have masses 3m,m and 2m, the friction is absent, the masses of the pulleys and the threads are negligible. Find the acceleration of mass 3m.
View Solutionfind the acceleration of the block of mass M in the situation shown in figure. All the surfaces are frictionless and the pulleys and the string are light.

View Solution
