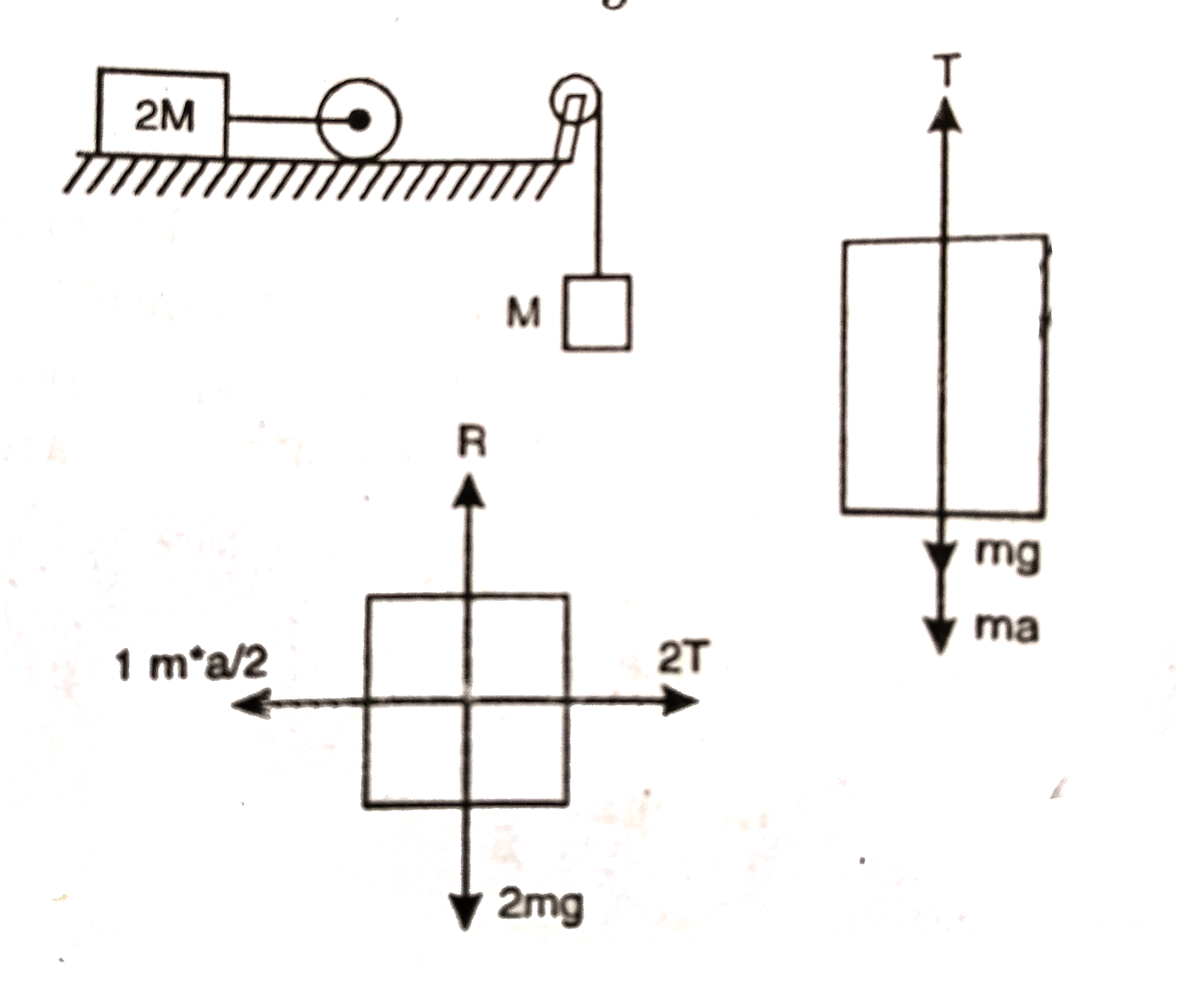
find the acceleration of the block of mass M in the situation shown in figure. All the surfaces are frictionless and the pulleys and the string are light.

Ma−2T=0.T+Ma−Mg=0
→Ma=2T
→Ma2+ma=Mg(∵T=Ma2)
>T=Ma2
→3Ma=2Mg
→a=2gg
 )
)
a. Acceleration of mas, <br>M=2g3
b. Tension,T=Ma2=M2×2g3=Mg3
c. Let, R=restant–––––oftensions<br>=forceexertedbytehclamponthep≤––––y<br> :. R'= sqrt(T^2+T^2)= sqrt(2) t<br>:. R= sqrt(2) T= ((sqrt(2) Mg)/3<br>again, tan theta = T/T=1<br>rarr theta = 45^0<br>Soitis(sqrt(2)Mg)/3atan∠of45^0 with horizontal.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Objective 2
9 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMACHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Short Answer
15 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises
34 Videos
Similar Questions
Find the acceleration of each block in the situation shown in the figure. All the surface are smooth and the pulleys and sttings are light.

View SolutionFind the acceleration of two masses as shown in figure . The pulley are light and frictionless and string are light and frictionless and string are light and inextensible.

View Solution
Knowledge Check
Find the acceleration of the 6 kg block in the figure. All the surfaces and pulleys are smooth. Also the strings are inextensible and light. [Take g=10m/s2]
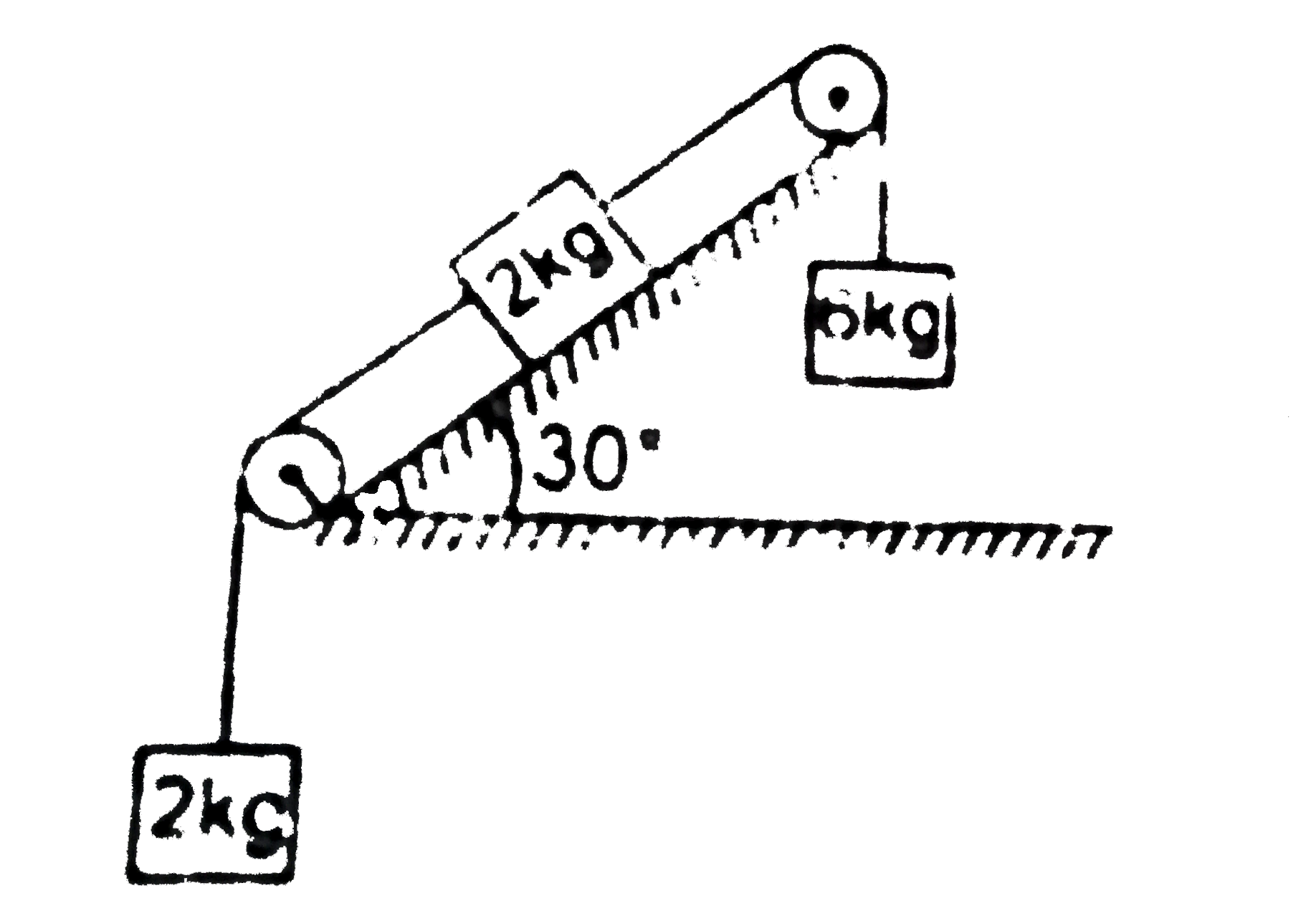 .A3m/s2B4m/s2C5m/s2D2m/s2
.A3m/s2B4m/s2C5m/s2D2m/s2The acceleration of the block (A) and (B) respectively in situation shown in the figure is: (pulleys and string are massless).
 A2g7 downward, g7 upwardB2g3 downward, g3 upwardC1013g downward, 5g13 upwardDnone of these
A2g7 downward, g7 upwardB2g3 downward, g3 upwardC1013g downward, 5g13 upwardDnone of these
Three blocks of masses m1,m2andm3 are connected as shown in the figure. All the surfaces are frictionless and the string and the pulleys are light. Find the acceleration of m1
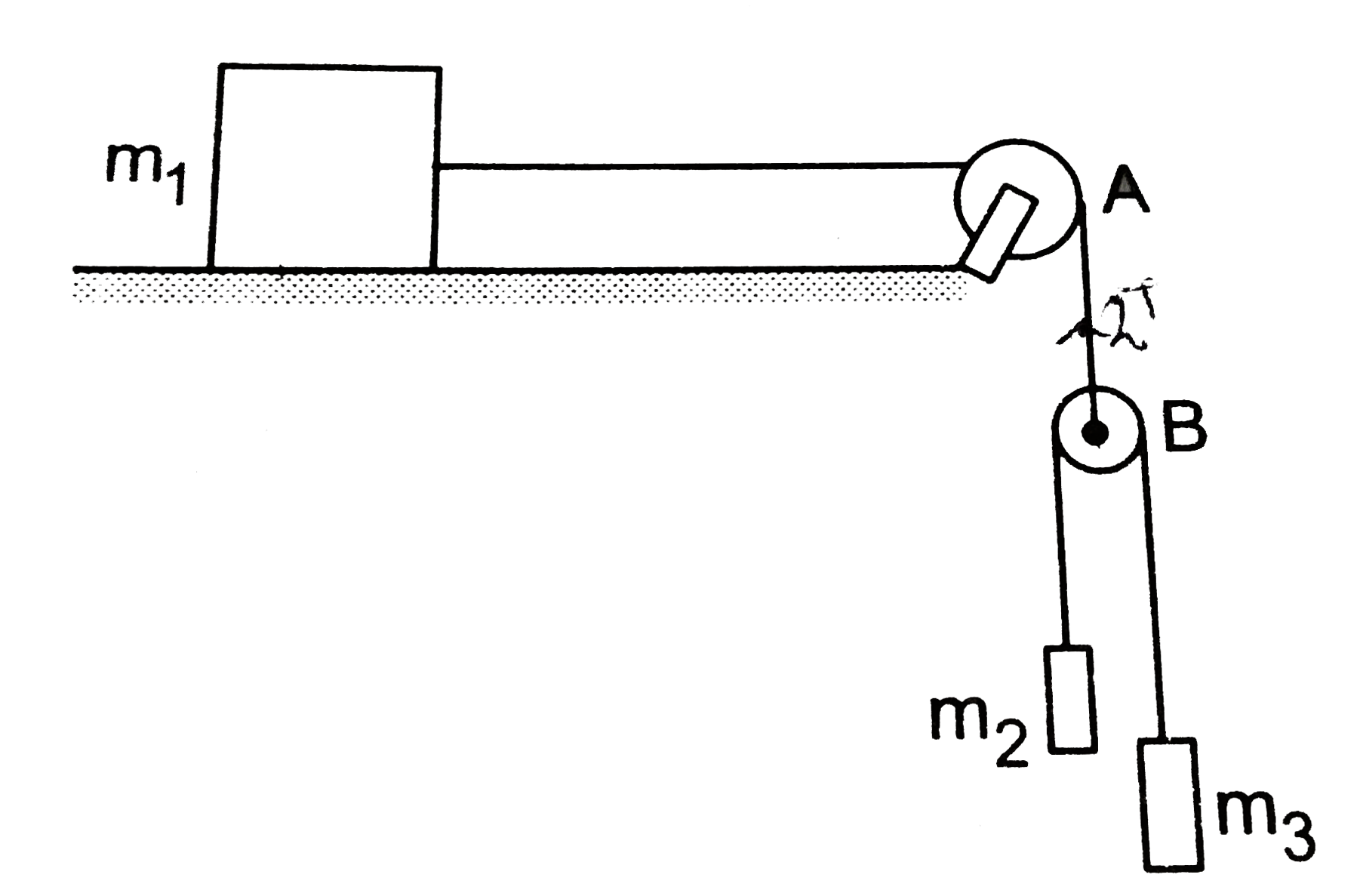
View SolutionFind the acceleration of the block of mass m in the arrangement shown in the following figures. The masses of the pulleys and the threads, as well as the friction are assumed to be negligible.

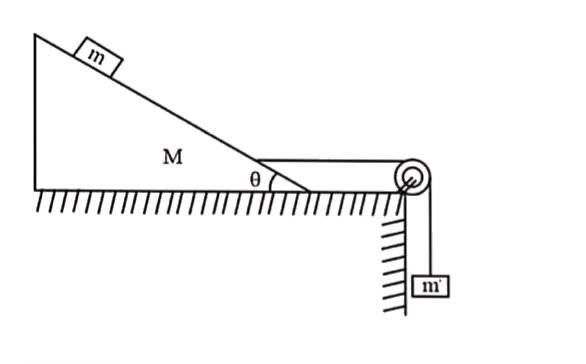
View SolutionFind the mass of the hanging block in which will prevent the smaller block of mass m from slipping over the triangular block of mass M. All the surfaces are frictionless and the strings and the pulleys are light

View Solution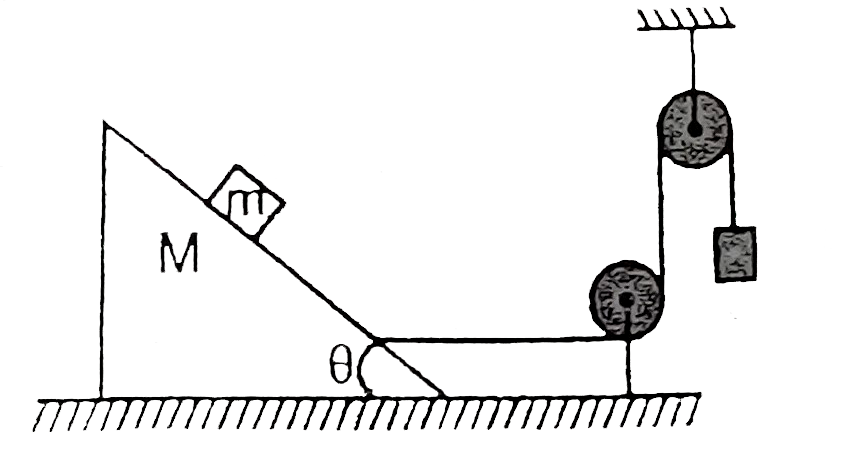
Find the mass (in kg) of the hanging block which will prevent the smaller block from slipping over the triangular block. All the surfaces are frictionless and the strings and the pulleys are light. Given m=M=1kg,cotθ=2,
View SolutionA hanging block of mass m' prevents the smaller block of mass m from slipping over a movable triangular block of mass M. All the surface are frictionless and the strings and the pulleys are light. Value of mass m' in terms of m, M and θ is
View SolutionConsider the situation shown in figure. All the surfaces are frictions and the string and the pulley are light. Find the magnitude of the acceleration of the two blocks.

View Solution
