A rabbit runs across a parking lot on which a set of coordinate axes has, strangely enough, been drawn . The coordinates (meters) of the rabbits position as functions of time t (seconds) are given by
and
(a) At t =15 s , what is the rabbits position vector in univector notation and in magnitude - angle notation ?
To solve the problem, we will follow these steps:
Step 1: Calculate the x-coordinate at t = 15 s
The x-coordinate is given by the equation:
x=0.31t2+7.2t+28
Substituting t=15:
x=0.31(152)+7.2(15)+28
Calculating 152=225:
x=0.31(225)+7.2(15)+28
Calculating 0.31×225=69.75 and 7.2×15=108:
x=69.75+108+28=205.75 m
Step 2: Calculate the y-coordinate at t = 15 s
The y-coordinate is given by the equation:
y=0.22t2−9.1t+30
Substituting t=15:
y=0.22(152)−9.1(15)+30
Using 152=225:
y=0.22(225)−9.1(15)+30
Calculating 0.22×225=49.5 and 9.1×15=136.5:
y=49.5−136.5+30=−57 m
Step 3: Write the position vector in unit vector notation
The position vector →r can be expressed as:
→r=x^i+y^j=205.75^i−57^j m
Step 4: Calculate the magnitude of the position vector
The magnitude |→r| is given by:
|→r|=√x2+y2
Substituting the values:
|→r|=√(205.75)2+(−57)2
Calculating (205.75)2=42329.0625 and (−57)2=3249:
|→r|=√42329.0625+3249=√45578.0625≈213.5 m
Step 5: Calculate the angle of the position vector
The angle θ can be calculated using:
tan(θ)=yx
Substituting the values:
tan(θ)=−57205.75
Calculating θ:
θ=tan−1(−57205.75)≈−15.6∘
Final Answer
The position vector in unit vector notation is:
→r=205.75^i−57^j m
The magnitude of the position vector is:
|→r|≈213.5 m
The angle of the position vector is:
θ≈−15.6∘
The x-coordinate is given by the equation:
x=0.31t2+7.2t+28
x=0.31(152)+7.2(15)+28
Calculating 152=225:
x=0.31(225)+7.2(15)+28
Calculating 0.31×225=69.75 and 7.2×15=108:
x=69.75+108+28=205.75 m
The y-coordinate is given by the equation:
y=0.22t2−9.1t+30
y=0.22(152)−9.1(15)+30
Using 152=225:
y=0.22(225)−9.1(15)+30
Calculating 0.22×225=49.5 and 9.1×15=136.5:
y=49.5−136.5+30=−57 m
The position vector →r can be expressed as:
→r=x^i+y^j=205.75^i−57^j m
The magnitude |→r| is given by:
|→r|=√x2+y2
Substituting the values:
|→r|=√(205.75)2+(−57)2
Calculating (205.75)2=42329.0625 and (−57)2=3249:
|→r|=√42329.0625+3249=√45578.0625≈213.5 m
The angle θ can be calculated using:
tan(θ)=yx
Substituting the values:
tan(θ)=−57205.75
Calculating θ:
θ=tan−1(−57205.75)≈−15.6∘
The position vector in unit vector notation is:
→r=205.75^i−57^j m
The magnitude of the position vector is:
|→r|≈213.5 m
The angle of the position vector is:
θ≈−15.6∘
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - CHECKPOINT3videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PROBLEMS50videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )3videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions57videos
OSCILLATIONS
Similar Questions
A rabbit runs across a parking lot on which a set of coordinate axes has, strangely enough, been drawn . The coordinates (meters) of the rabbits position as functions of time t (seconds) are given by
x=−0.31t2+7.2t+28
and y=0.22t2−9.1t+30
For the rabbit in the precending sample problem , find the velocity →v at time t = 15s .View SolutionA rabbit runs across a parking lot on which a set of coordinate axes has, strangely enough, been drawn . The coordinates (meters) of the rabbits position as functions of time t (seconds) are given by
x=−0.31t2+7.2t+28
and y=0.22t2−9.1t+30
For the rabbit in the precending sample problem find the acceleration →a at time t = 15 sView Solution
Knowledge Check
- Question 1 - Select One
Let the function y = f(x) be given by
x=t5−5t3−20t+7
andy=4t3−3t2−18t+3
where t∈(−2,2) then f'(x) at t = 1 isA52B25C75D57 - Question 2 - Select One
The coordinates of a moving particle at any time t are given by, x=2t3 and y=3t3. Acceleration of the particle is given by
A468tBt√468C234t2Dt√234 - Question 3 - Select One
The x and y coordinates of a particle at any time t are given by x=2t+4t2andy=5t , where x and y are in metre and t in second. The acceleration of the particle at t = 5 s is
A40ms−2B20ms−2C8ms−2Dzero
Figure shows the x coordinate of a particle as a function of time. Find the signs of vxandaxatt=t1, t=t_2 and t=t_3.
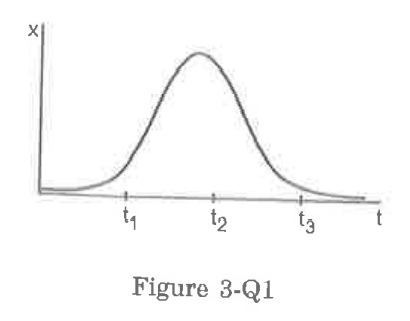 View Solution
View SolutionFind the locus of a point whose coordinate are given by x=t+t2,y=2t+1, where t is variable.
View SolutionEach of the four particles move along an x axis. Their coordinates (in metres) as function of time (in seconds) are given by Particle 1 : x(t) = 3.5 - 2.7t3 Particle 2 : x(t) = 3.5 + 2.7t3 Particle 3 : x(t) = 3.5 + 2.7t2 Particle 4 : x(t) = 2.5 - 3.4t - 2.7 t2 which of these particles is speeding up for t > 0?
View SolutionEach of four particles moves along an x axis. Their coordinates (in meters) as function of time (in seconds) are given by
Particle 1:x(t)=3.5−2.7t3
Particle :2 x(t)=3.5+2.7t3
particle 3: x(t)=3.5+2.7t2
particle 4: x(t)=3.5−3.4t−2.7t2
Which of these particles have constant acceleration ?View SolutionThe coordinates of a moving particle at any time t are given by x=αt3 and y=βt3. The speed of the particle at time t is given by
View Solution

