A radio can be turned over a frequency range from 500kHz→1.5MHz. If its L-C circuit has an effective inductance of 400(μ)H, what is the range of its variable capacitor.
To solve the problem of determining the range of the variable capacitor in the radio's L-C circuit, we can follow these steps:
Step 1: Understand the relationship between frequency, inductance, and capacitance
The resonant frequency f of an L-C circuit is given by the formula:
f=12π√LC
Where:
- f is the frequency in hertz (Hz)
- L is the inductance in henries (H)
- C is the capacitance in farads (F)
Step 2: Rearrange the formula to find capacitance
We can rearrange the formula to express capacitance C in terms of frequency f and inductance L:
C=1(2πf)2L
Step 3: Identify the given values
From the problem, we have:
- Inductance L=400μH=400×10−6H
- Frequency range:
- f1=500kHz=500×103Hz
- f2=1.5MHz=1.5×106Hz
Step 4: Calculate the capacitance at the lower frequency f1
Using the formula for capacitance:
C1=1(2πf1)2L
Substituting the values:
C1=1(2π×500×103)2×(400×10−6)
Calculating C1:
1. Calculate 2π×500×103:
2π×500×103≈3141592.65Hz
2. Square this value:
(3141592.65)2≈9.8696×1012Hz2
3. Now calculate C1:
C1=19.8696×1012×400×10−6≈2.54×10−12F
Step 5: Calculate the capacitance at the upper frequency f2
Using the same formula:
C2=1(2πf2)2L
Substituting the values:
C2=1(2π×1.5×106)2×(400×10−6)
Calculating C2:
1. Calculate 2π×1.5×106:
2π×1.5×106≈9424778.76Hz
2. Square this value:
(9424778.76)2≈8.87×1013Hz2
3. Now calculate C2:
C2=18.87×1013×400×10−6≈2.82×10−12F
Step 6: Determine the range of the variable capacitor
The range of the variable capacitor C is from C1 to C2:
C ranges from 2.54×10−12F to 2.82×10−12F
Final Answer
The range of the variable capacitor is approximately:
C ranges from 2.54pF to 2.82pF
---
The resonant frequency f of an L-C circuit is given by the formula:
f=12π√LC
Where:
- f is the frequency in hertz (Hz)
- L is the inductance in henries (H)
- C is the capacitance in farads (F)
We can rearrange the formula to express capacitance C in terms of frequency f and inductance L:
C=1(2πf)2L
From the problem, we have:
- Inductance L=400μH=400×10−6H
- Frequency range:
- f1=500kHz=500×103Hz
- f2=1.5MHz=1.5×106Hz
Using the formula for capacitance:
C1=1(2πf1)2L
Substituting the values:
C1=1(2π×500×103)2×(400×10−6)
1. Calculate 2π×500×103:
2π×500×103≈3141592.65Hz
2. Square this value:
(3141592.65)2≈9.8696×1012Hz2
3. Now calculate C1:
C1=19.8696×1012×400×10−6≈2.54×10−12F
Using the same formula:
C2=1(2πf2)2L
Substituting the values:
C2=1(2π×1.5×106)2×(400×10−6)
1. Calculate 2π×1.5×106:
2π×1.5×106≈9424778.76Hz
2. Square this value:
(9424778.76)2≈8.87×1013Hz2
3. Now calculate C2:
C2=18.87×1013×400×10−6≈2.82×10−12F
The range of the variable capacitor C is from C1 to C2:
C ranges from 2.54×10−12F to 2.82×10−12F
The range of the variable capacitor is approximately:
C ranges from 2.54pF to 2.82pF
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercise 5.1
15 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Subjective
15 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Single Correct
10 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.3
15 Videos
Similar Questions
A radio can tune over the frequency range of a portion of MW broadcast band (800 kHz to 1200 kHz). If its LC circuit has an effective inductance of 200μH, what must be the range of its variable capacitor ?
View SolutionA radio can tune over the frequency range of a portion of MW broadcast band (800 kHz to 1200 kHz). If its LC circuit has an effective inductance of 200μH, what must be the range of its varialbe capacitor ?
View Solution
Knowledge Check
A series LCR circuit with R=20Ω,L=1.5H and C=35μF is connected to a variable frequency 200V ac supply. When the frequency of the supply equals the natural frequency of the circuit, what is the average power in kW transferred to the circuit in one complete cycle?
A200 WB2000 WC100 WD4000 W
An alternating emf of 110 V is applied to a circuit containing a resistance R of 80Ω and an inductor L in series. The current is found to lag behind the supply voltage by an angle θ=tan1(3/4). Find the :
If the inductor has a coefficient of self inductance of 0.1 H, what is the frequency of the applied emf ?
View SolutionIn an L−C−R ereis circuit R=150Ω,L=0.0750H and C=0.0180μF . The source has voltage amplitude V=150V and a frequencey equal to the resonacne frequency of the circuit.
(a) What is the power factor ?
(b) What is the average power delivered by the source?
(c) The capacitor is replaced by one with C=0.0360μF and the source frequency is adjusted to the new resonance value. Then, what is the average power delivered by the source?
View SolutionAn L−C−R series circuit with L=0.120H,R=240a, and C=7.30μF carries an rms current of 0.450A with a frequency of 400Hz.
(a) What are the phase angle and power factor for this circuit?
(b) What is the impedance of the circuit?
(c) What is the rms voltage of the source?
(d) What average power is delivered by the source?
(e) What is the average rate at which electrical energy is converted to thermal energy in the resistor?
(f) What is the average rate at which electrical energy is dissipated ( converted to other forms) in the capacitor?
(g) In the inductor ?
View SolutionAn alternating emf of 110 V is applied to a circuit containing a resistance R of 80Ω and an inductor L in series. The current is found to lag behind the supply voltage by an angle θ=tan−1(3/4). Find the :
(i) Inductive reactance
(ii) Impedance of the circuit
(iii) Current flowing in the circuit
(iv) If the inductor has a coefficient of self inductance of 0.1 H. What is the frequency of the applied emf?
View SolutionA series LCR circuit with R=20Ω,L=1.5H and C=35μF is connected to a variable frequency 200V ac supply. When the frequency of the supply equals the natural frequency of the circuit, what is the average power in kW transferred to the circuit in one complete cycle?
View SolutionThe current in a discharging LR circuit without the battery drops from 2.0 A to 1.0A in 0.10 s. (a) find the time constant of the circuit. (b) if the inductance of the circuit is 4.0 H, what is its resistance?
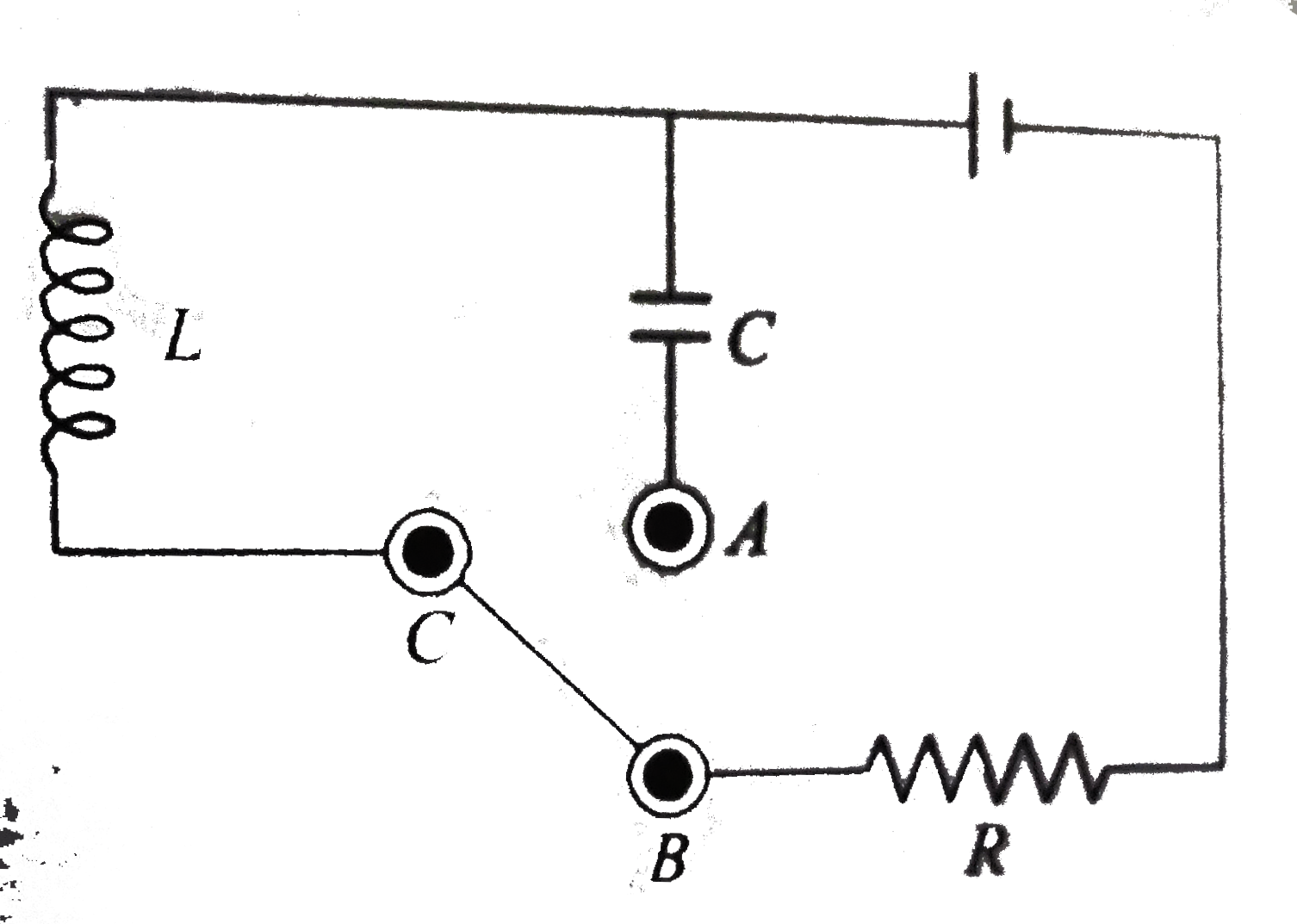
View SolutionIn the circuit shows in Fig the capacitor is initially uncharged and the two - way switch is connected in the position BC. Find the current through the resistence R as a function of time t. After time t=4 ms, the switch is connected in the position AC. Find the frequency of oscillation of the capacitor of the circuit in the position, and the maximum charge on the capacitor C. At what time will the energy stored in the capacitor be one-half of the total energy stored in the circuit? It is given L=2×10−4H,C=5mF,R=In210Ω and emf of the battery =1V.
View Solution
