The current in a discharging LR circuit without the battery drops from 2.0 A to 1.0A in 0.10 s. (a) find the time constant of the circuit. (b) if the inductance of the circuit is 4.0 H, what is its resistance?
To solve the problem step by step, we will break it down into two parts as per the question.
Part (a): Finding the Time Constant of the Circuit
1. Identify the given values:
- Initial current, I0=2.0A
- Current after time t=0.1s, I=1.0A
- Time, t=0.1s
2. Use the formula for current in a discharging LR circuit:
I=I0e−tτ
where τ is the time constant.
3. Substitute the known values into the equation:
1.0=2.0e−0.1τ
4. Rearrange the equation to isolate the exponential term:
1.02.0=e−0.1τ
12=e−0.1τ
5. Take the natural logarithm of both sides:
ln(12)=−0.1τ
6. Use the property of logarithms:
ln(12)=−ln(2)
Therefore,
−ln(2)=−0.1τ
7. Remove the negative signs:
ln(2)=0.1τ
8. Rearrange to solve for τ:
τ=0.1ln(2)
9. Calculate ln(2):
ln(2)≈0.693
10. Substitute ln(2) back into the equation:
τ=0.10.693≈0.144s
Answer for Part (a):
The time constant τ of the circuit is approximately 0.144 seconds.
---
Part (b): Finding the Resistance of the Circuit
1. Identify the given values:
- Inductance, L=4.0H
- Time constant, τ=0.144s (from Part (a))
2. Use the formula relating time constant, inductance, and resistance:
τ=LR
3. Rearrange the formula to solve for resistance R:
R=Lτ
4. Substitute the known values:
R=4.0H0.144s
5. Calculate R:
R≈27.78Ω
Answer for Part (b):
The resistance R of the circuit is approximately 27.78 ohms, which can be rounded to 28 ohms.
---
- Initial current, I0=2.0A
- Current after time t=0.1s, I=1.0A
- Time, t=0.1s
I=I0e−tτ
where τ is the time constant.
1.0=2.0e−0.1τ
1.02.0=e−0.1τ
12=e−0.1τ
ln(12)=−0.1τ
ln(12)=−ln(2)
Therefore,
−ln(2)=−0.1τ
ln(2)=0.1τ
τ=0.1ln(2)
ln(2)≈0.693
τ=0.10.693≈0.144s
The time constant τ of the circuit is approximately 0.144 seconds.
- Inductance, L=4.0H
- Time constant, τ=0.144s (from Part (a))
τ=LR
R=Lτ
R=4.0H0.144s
R≈27.78Ω
The resistance R of the circuit is approximately 27.78 ohms, which can be rounded to 28 ohms.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 2
10 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 2
7 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise
8 Videos
Similar Questions
The current in a discharging LR circuit is given by I=i0(tτ) where τ is the time constant of the circuit. Calculate the rms current for the period t=0 to t=τ.
View SolutionThe current in a discharging LR circuit is given by I=i0e−tτ where τ is the time constant of the circuit. Calculate the rms current for the period t=0 to t=τ.
View SolutionIn an LR circuit, current at t=0 is 20A . After 2s it reduced to 18A. The time constant of the circuit is (in second)
View SolutionCurrent in a circuit falls form 0.5 A to 0.0 A in 0.1 s. If an average e.m.f. of 200 V is induced, give an estimate of the self inductance of the circuit ?
View SolutionA coil of inductance 2H and resistance 10Ω are in a series circuit with an open key and a cell of constant 100V with negligible resistance. At time i=0, the key is closed. Find
(a) the time constant of the circuit.
(b) the maximum steady current in the circuit.
(c) the current in the circuit at f=1s.
View SolutionIn a series RC circuit having battery of 12 V, capacitor is charged from O to 6 V in 0.1 s. Find value of resistance R.
View SolutionA coil carrying a steady current is short-circuited. The current in it decreases α times in time t0. The time constant of the circuit is
View SolutionThe electric curren in a charging R-C circuit is given by i=i0e−tRC when i0, R and C aere constant parameters of the circuit and t is time. Find the rate of change of current at a.t=0,b.t=RCc.t=10RC.
View Solution_S01_049_Q01.png)
If current in given circuit is 0.1 A then calculate resistance of P-N junction.
View SolutionIn the circuit as shown if the current drawn through battery is 0.5A. Then
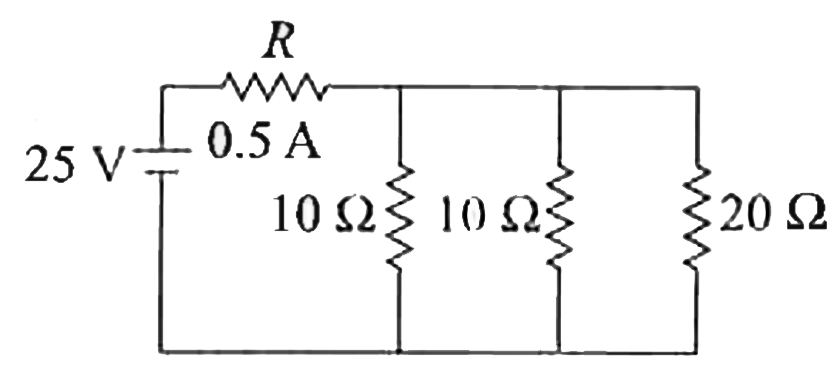
View Solution
