Question

A railway track runs parallel to a road until a turn brings the road to railway corssing. A cyclist rides along the road every day at a constant speed $20km/hr$. He normally meets a train that travels in same direction at the crossing. One day he was late by $25$ minutes and met the train $10km$ before the railway crossing. Find the speed of the train.

Answer

`120 km h^(-1)`

Explanation

Method 1: If on day the man is `25 min` late he will reach `B` at time `t+25` m.
.
But form `C` and to `B`, he takes `30 min` Hence, the time at position `C` will be `t+25-30 =(t-5) min`, The train is runnuing right time it will reach at time at time `t`. Hence, time taken by train to reach from`C` to `B` is ` 5 min`. Hence, speed of trains is
`v_(train) =(10)/(5) =2km min^(-1)=120 km h^(-2)`
Meghod 2:
.
Hence, speed of rain `v_(traom)=(10 km)/(5 min) =2 km min^(-1)`
`=120 km h^(-1)`
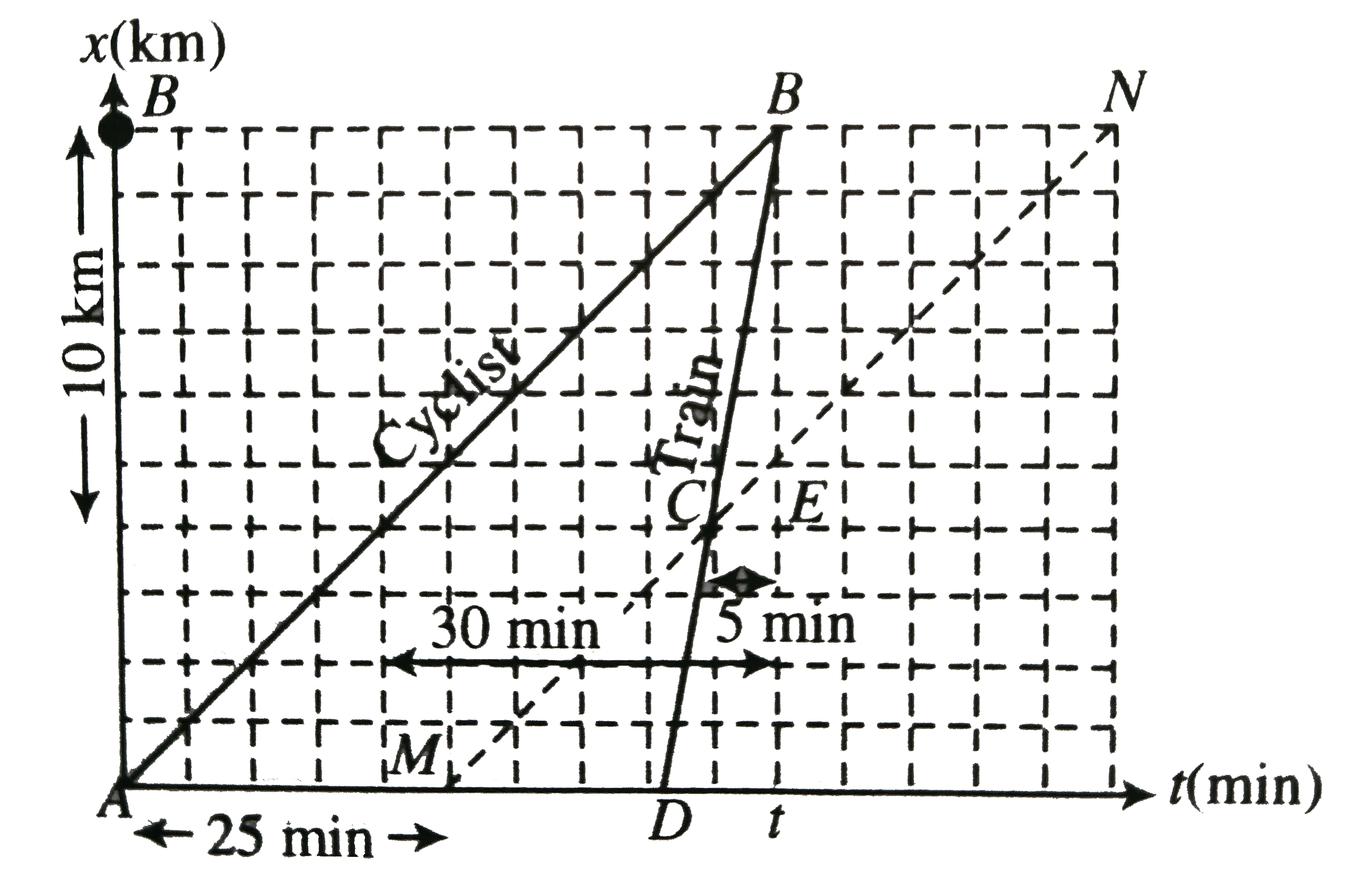
The slope of position-time graph gives velocity. The velocity of cyclist is less than velocity of train, `AB` line represents the motion of cyclist and line `BD` represents motion of the train.
Hence, the slope of `AB` is less than the slope of `BD`.
Both lines meet at point `B`, at this position rrain meets cyclist every day
One day cyclist is `25 min` late, i.e. the cyclist starts `25 min` after regulat time when he starts.
The line `DB` shifted paralled to itself by `25 min`, i.e. line `M'N'` represents the motion of cyclist. The line `M'N'` cuts the line `BD` at `C, C` is the position wher train crosses the cyclist at the day when cyclist is late.
Time taken by to move from `C` to crossing,
`t_(CB) =(10)/(20)=(1)/(2) m= min`
Hence, velocity of the train, `v_(traon) =(10)/((5//60)) =120 km h^(-1)`.