A raindrop as it falls through for or mist collects mass at a uniform rate. The drop starts from rest with zero radius and remains spherical at all times. The acceleration with which it falls
is constant and equal to g/2
is constant and equal to g/3
increases with me
decreases with time
To solve the problem of determining the acceleration of a raindrop as it falls through mist while collecting mass at a uniform rate, we will follow these steps:
Step 1: Understand the Forces Acting on the Raindrop
The raindrop experiences two main forces:
- The weight of the raindrop acting downward, which is given by mg (where m is the mass of the raindrop and g is the acceleration due to gravity).
- The thrust force acting upward due to the drag from the air, which can be expressed as Fthrust=Vdmdt (where V is the velocity of the raindrop and dmdt is the rate of mass change).
Step 2: Write the Net Force Equation
The net force acting on the raindrop can be expressed as:
Fnet=mg−Fthrust=mg−Vdmdt
According to Newton's second law, this net force can also be expressed as:
Fnet=ma=mdvdt
Thus, we can set the two expressions for net force equal to each other:
mdvdt=mg−Vdmdt
Step 3: Substitute for Mass Change
Given that the raindrop collects mass at a uniform rate, we can denote the rate of mass change as dmdt=k (a constant). Therefore, we can express the mass m as:
m=kt
where k is a constant that relates to the rate of mass collection.
Step 4: Substitute into the Net Force Equation
Substituting m=kt into the net force equation gives:
ktdvdt=kgt−Vk
Dividing through by k (assuming k≠0):
tdvdt=gt−V
Step 5: Rearranging the Equation
Rearranging the equation yields:
tdvdt+V=gt
This can be rewritten as:
tdvdt=gt−V
Step 6: Integrate the Equation
To find the relationship between velocity and time, we can integrate:
∫tdvdtdt=∫(gt−V)dt
This leads to:
vt=12gt2+C
where C is a constant of integration. Since the raindrop starts from rest, we can set C=0.
Step 7: Solve for Velocity
Thus, we find:
Vt=12gt2
Solving for V:
V=gt2
Step 8: Calculate Acceleration
The acceleration a is given by:
a=dvdt
Differentiating V=gt2 with respect to t:
a=g2
Conclusion
The acceleration of the raindrop as it falls through mist while collecting mass at a uniform rate is:
a=g2
The raindrop experiences two main forces:
- The weight of the raindrop acting downward, which is given by mg (where m is the mass of the raindrop and g is the acceleration due to gravity).
- The thrust force acting upward due to the drag from the air, which can be expressed as Fthrust=Vdmdt (where V is the velocity of the raindrop and dmdt is the rate of mass change).
The net force acting on the raindrop can be expressed as:
Fnet=mg−Fthrust=mg−Vdmdt
According to Newton's second law, this net force can also be expressed as:
Fnet=ma=mdvdt
Thus, we can set the two expressions for net force equal to each other:
mdvdt=mg−Vdmdt
Given that the raindrop collects mass at a uniform rate, we can denote the rate of mass change as dmdt=k (a constant). Therefore, we can express the mass m as:
m=kt
where k is a constant that relates to the rate of mass collection.
Substituting m=kt into the net force equation gives:
ktdvdt=kgt−Vk
Dividing through by k (assuming k≠0):
tdvdt=gt−V
Rearranging the equation yields:
tdvdt+V=gt
This can be rewritten as:
tdvdt=gt−V
To find the relationship between velocity and time, we can integrate:
∫tdvdtdt=∫(gt−V)dt
This leads to:
vt=12gt2+C
where C is a constant of integration. Since the raindrop starts from rest, we can set C=0.
Thus, we find:
Vt=12gt2
Solving for V:
V=gt2
The acceleration a is given by:
a=dvdt
Differentiating V=gt2 with respect to t:
a=g2
The acceleration of the raindrop as it falls through mist while collecting mass at a uniform rate is:
a=g2
Topper's Solved these Questions
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - More a than one option is Correct
1 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
Similar Questions
If a body starts from rest, the time in which it covers a particular displacement with uniform acceleration is :
View SolutionA particle start from rest, with uniform acceleration at time t, choose the correct option
View SolutionA small drop of water falls from rest through a large height h in air, the final velocity is
View SolutionA spherical planet far out in space has mass 2M and radius a. A particle of mass m is falling freely near its surface. What will be the acceleration of that particle ?
View SolutionA mass M is supported by a massless string wound round a uniform cylinder ofmass M and radius R. On releasing the mass from rest, it will fall with acceleration?

View SolutionAcidified water from certain reservoir kept at a potential V falls in the form of small droplets each of radius r through a hole into a hollow conducting sphere of radius a. The sphere is insulated and is initially at zero potential. If the drops continue to fall untill the sphere is half full, the potential acquired by the sphere is
View SolutionA uniform disc of mass M and radius R is mounted on a fixed horizontal axis. A block of mass m hangs from a massless string that is wrapped around the rim of the disc. The magnitude of the acceleration of the falling block (m) is
View SolutionWater drops fall from a tap on to the floor 5.0 m below at regular intervals of time. The first drop strikes the floor when the fifth drops beings to fall. The height at which the third drop will be from ground at the instant when the first drop strikes the ground is (takeg=10m−2)
View SolutionAn electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.0×104N/C(Fig.a)
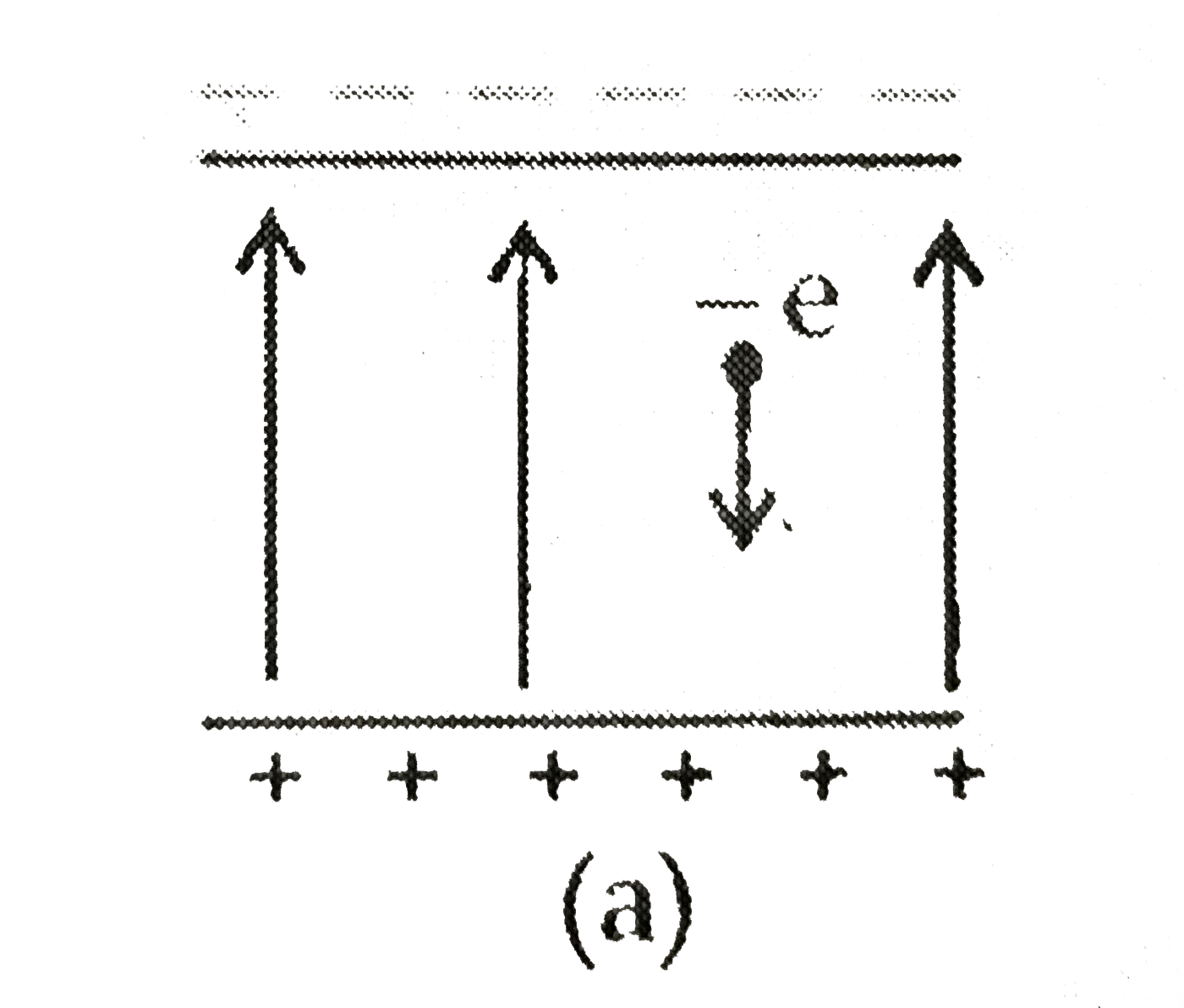
Calculate the time it takes to fall through this distance starting from rest. If the direction of the field is reversed (fig .b) keeping its magnitude unchanged , calculate the time taken by a proton to fall through this distance starting from rest.

View SolutionA body moves for a total of nine second starting from rest with uniform acceleration and then with uniform retardation, which is twice the value of acceleration and then stop. The duration of uniform acceleration is
View Solution
