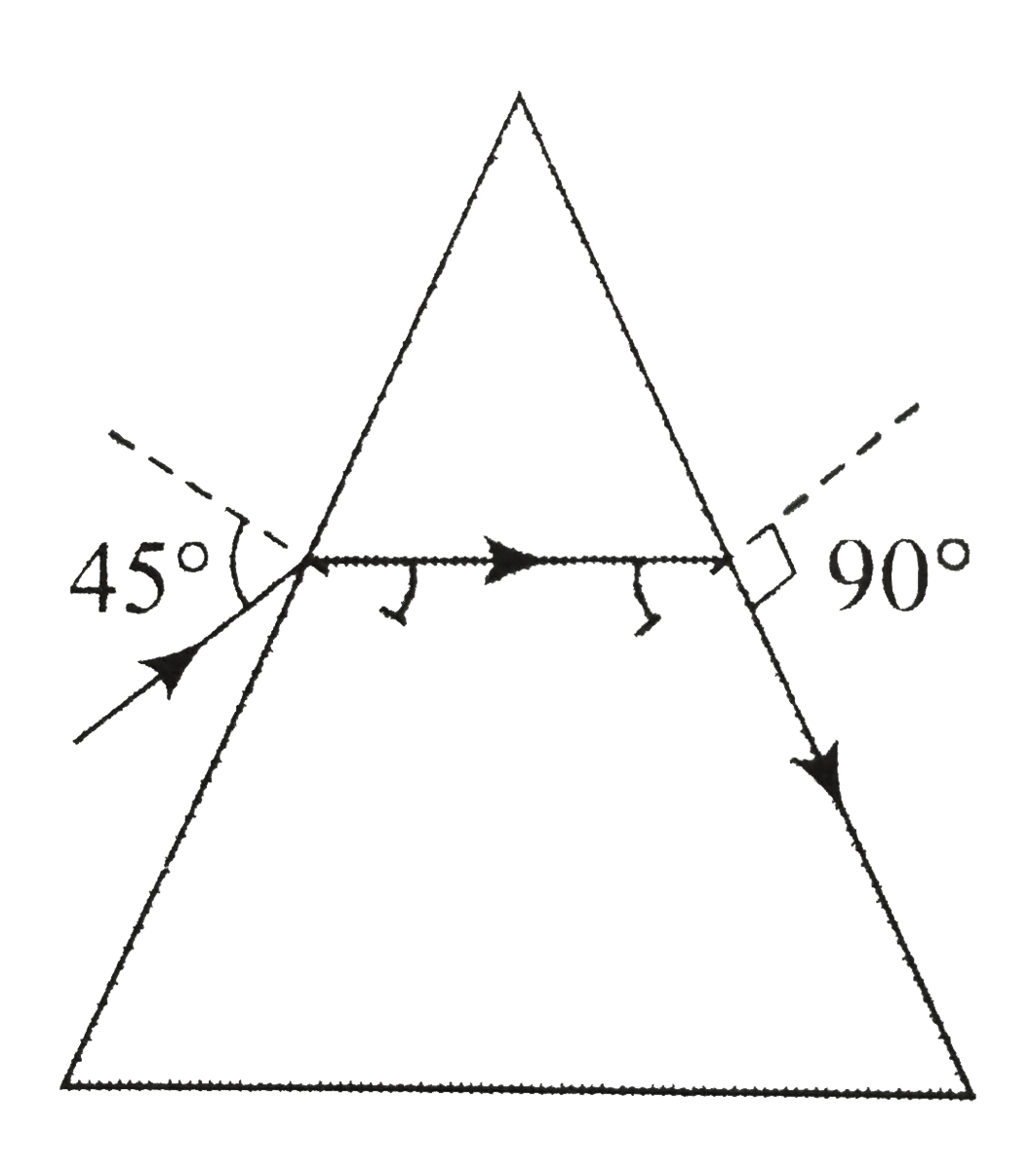
A ray is incident at an angle of incidence i on one surfcae of a small angle prism (with angle of prism A) and emerges normally from opposite surface. If refractive index of material of prism is μ then the angle of incidence is nearly equal to
A2μ
2Aμ
μA
μA2
To solve the problem, we need to find the angle of incidence i for a ray of light incident on a small angle prism with an angle A and refractive index μ. The ray emerges normally from the opposite surface of the prism.
1. Understanding the Geometry of the Prism:
- Let the angle of the prism be A.
- The ray is incident at an angle i on one surface of the prism and emerges normally from the opposite surface.
2. Using Snell's Law:
- At the first surface, we can apply Snell's law:
n1sin(i)=n2sin(r)
- Here, n1 (the refractive index of air) is approximately 1, and n2 (the refractive index of the prism) is μ.
- Therefore, we have:
sin(i)=μsin(r)
3. Considering Small Angles:
- Since the prism is small, we can use the small angle approximation:
sin(i)≈iandsin(r)≈r
- Thus, we can rewrite Snell's law as:
i≈μr
4. Analyzing the Geometry Inside the Prism:
- The ray emerges normally from the opposite surface, which means the angle of refraction r at the second surface is 90∘.
- The angle of incidence at the second surface is 90∘−r.
5. Using the Triangle Relationship:
- In the triangle formed by the angles at the prism, we have:
90∘+(90∘−r)+A=180∘
- Simplifying this gives:
180∘−r+A=180∘⟹r=A
6. Substituting Back:
- Now substituting r=A back into the equation i≈μr:
i≈μA
Final Answer:
The angle of incidence i is nearly equal to:
i≈μA
- Let the angle of the prism be A.
- The ray is incident at an angle i on one surface of the prism and emerges normally from the opposite surface.
- At the first surface, we can apply Snell's law:
n1sin(i)=n2sin(r)
- Here, n1 (the refractive index of air) is approximately 1, and n2 (the refractive index of the prism) is μ.
- Therefore, we have:
sin(i)=μsin(r)
- Since the prism is small, we can use the small angle approximation:
sin(i)≈iandsin(r)≈r
- Thus, we can rewrite Snell's law as:
i≈μr
- The ray emerges normally from the opposite surface, which means the angle of refraction r at the second surface is 90∘.
- The angle of incidence at the second surface is 90∘−r.
- In the triangle formed by the angles at the prism, we have:
90∘+(90∘−r)+A=180∘
- Simplifying this gives:
180∘−r+A=180∘⟹r=A
- Now substituting r=A back into the equation i≈μr:
i≈μA
The angle of incidence i is nearly equal to:
i≈μA
Topper's Solved these Questions
Similar Questions
A Ray of light is incident at an angle 60° on one face of a prism which has protecting angle of 30°. The emerging ray deviates through 30° from incident light. The refractive index of material of prism is
View SolutionIn an isosceles prism of prism angle 45∘, it is found that when the angle of incidence is same as the prism angle, the emergent ray grazes the emergent surface. Find the refractive index of the material of the prism.For what angle of incidence the angle of deviation will be minimum ?
View Solution
Knowledge Check
A ray is incident at an angle of incidence i on one surfcae of a small angle prism (with angle of prism A) and emerges normally from opposite surface. If refractive index of material of prism is μ then the angle of incidence is nearly equal to
A2AμBμAC2A2DA2μA ray is ihncident at an angle of incidence ii on one surface of a prism of small angle A and emerge normally from opposite surface. If the refractive index of the material of prism is μ. the angel of incidance I is nearly equal to
AAμBA2μCμADμA2A ray of light is incident at an angle of 60∘ on one face of a prism of angle 30∘. They ray emerges normally from the other face of the prism. The refractive index of the prism material is
A√2B√3C2D3
In an isosceles prism of angle 45∘, it is found that when the angle of incidence is same as the prism angle, the emergen ray grazes the emergent surface.
Find the refractive index of the material of the prism. For what angle of incidenc, the angle of deviation will be minimum?
View SolutionWhen a ray of light falls on a prism of angle 48∘ , it suffers minimum deviation. Refractive index of the material of prism is 1.6. The angle of incidence is nearly
View SolutionA ray of light is incident normally on one face of a right-angled isosceles prism and then it grazes the hypotenuse. The refractive index of the material of the prism is
View SolutionA ray of light incident at an angle θ on a refracting face of a prism emerges from the other face normally. If the angle of the prism is 5∘ and the prism is made of a material of refractive index 1.5, the angle of incidence is.
View SolutionA ray of light is incident at 65∘ on one face of a prism of angle of 30∘ and the emergent ray makes 35∘ with the incident ray. The refractive index of the prism is:
View Solution
