A ray of light on a transparent sphere with centre C as shown in the figure. The ray emerges from sphere parallel to line AB. The refractive index of sphere is

Deviation by a sphere is 2(i−r)
Here, deviation δ=60∘=2(i−r)
or i−r=30∘
⇒r=i−30∘=60∘−30∘=30∘
∴μ=sinisinr=sin60∘sin30∘=√3
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.6
15 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.7
21 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.4
12 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
A ray of light falls on a transparent sphere with centre at C as shown in figure. The ray emerges from the sphere parallel to line AB. The refractive index of the sphere is

View SolutionA ray of light falls on a transparent sphere with centre at C as shown in figure. The ray emerges from the sphere parallel to line AB. The refractive index of the sphere is

View Solution
Knowledge Check
A rays of light is incident on a thick slab of glass of thickness t as shown in figure. The emergent ray is parallel to the incident ray but displaced sideways by a distance d. If the angles are small then d is
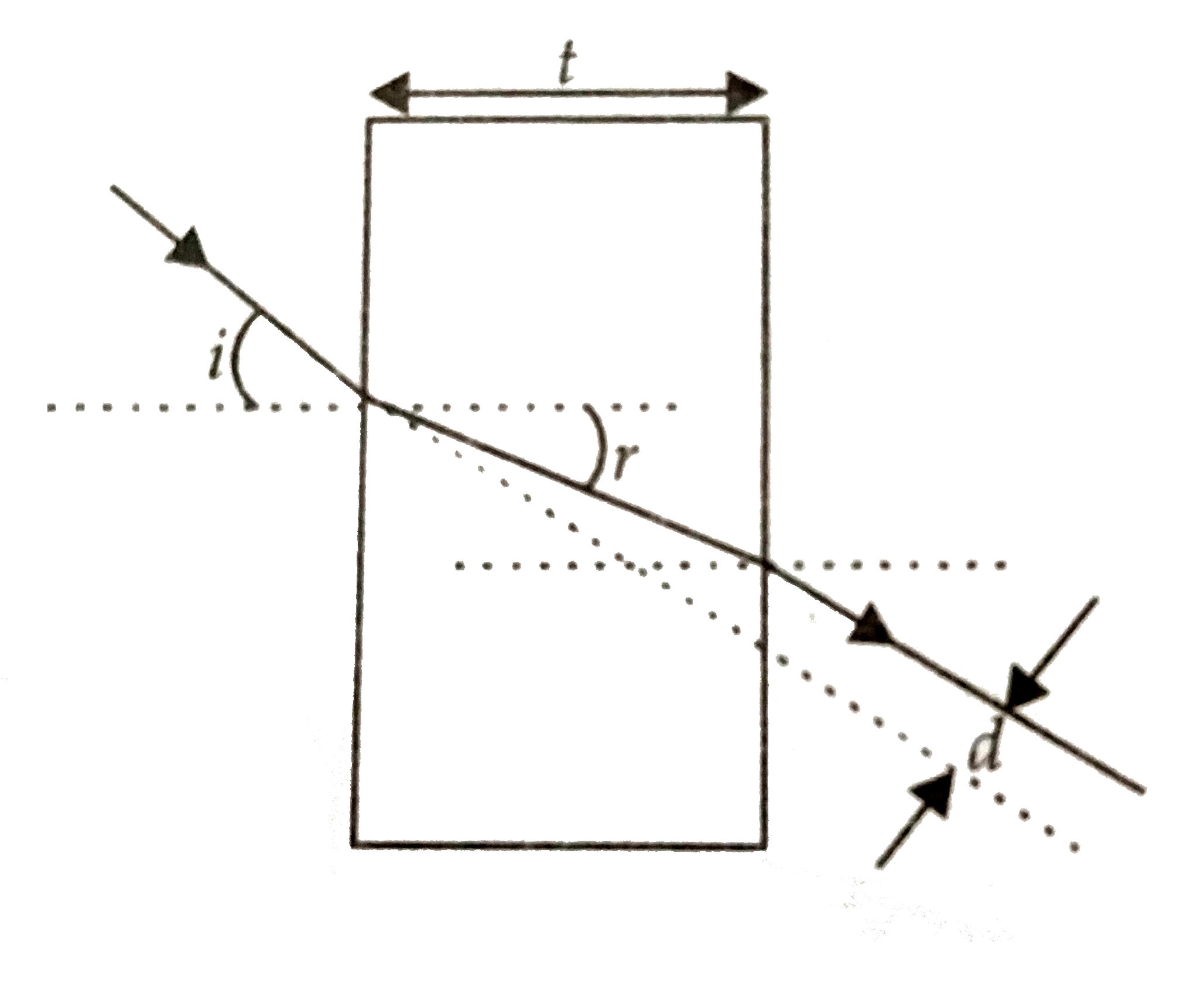 At(1+ir)Brt(1−ir)Cit(1−ri)Dt(1+ri)
At(1+ir)Brt(1−ir)Cit(1−ri)Dt(1+ri)
A ray of light falls on a transparent sphere with centre at C as shown in figure. The ray emerges from the sphere parallel to line AB. The refractive index of the sphere is

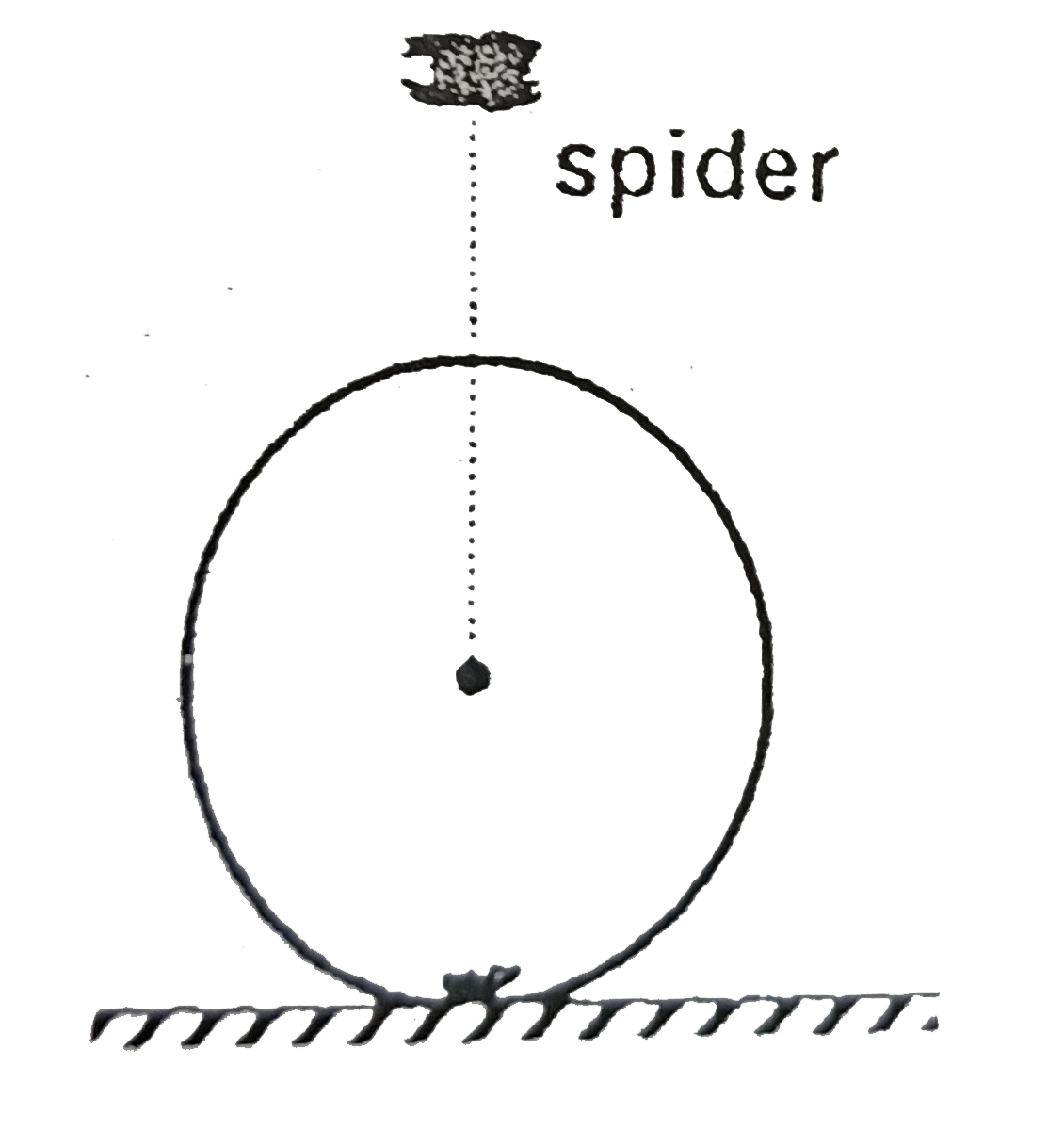
View SolutionA spider is hanging by means of its own silk thread directly above a transparent fixed sphere of radius R=20cm as shown in the figure. The refractive index of the material of the sphere is equal to √2 and the height of the spider from the centre of the sphere is 2R(=40cm). An insect, initially sitting at the bottom, starts crawling on the sphere along a vertical circular path with the constant speed of π/4cm/s. For how long time the insect will be invisible for the spider, assume that it crawls once round the vertical circle.
View SolutionA parallel beam of light emerges from the opposite surface of the sphere when a point source of light lies at the surface of the sphere. The refractive index of the sphere is
View SolutionA ray of light, travelling parallel to diameter of a sphere enters the sphere through a hole at point A as shown in the figure. The inner surface of the sphere is made perfectly reflecting. Find the number of reflections suffered by the ray before coming out of the sphere.

View SolutionA parallel beam of light falls on a solid tranparent sphere.
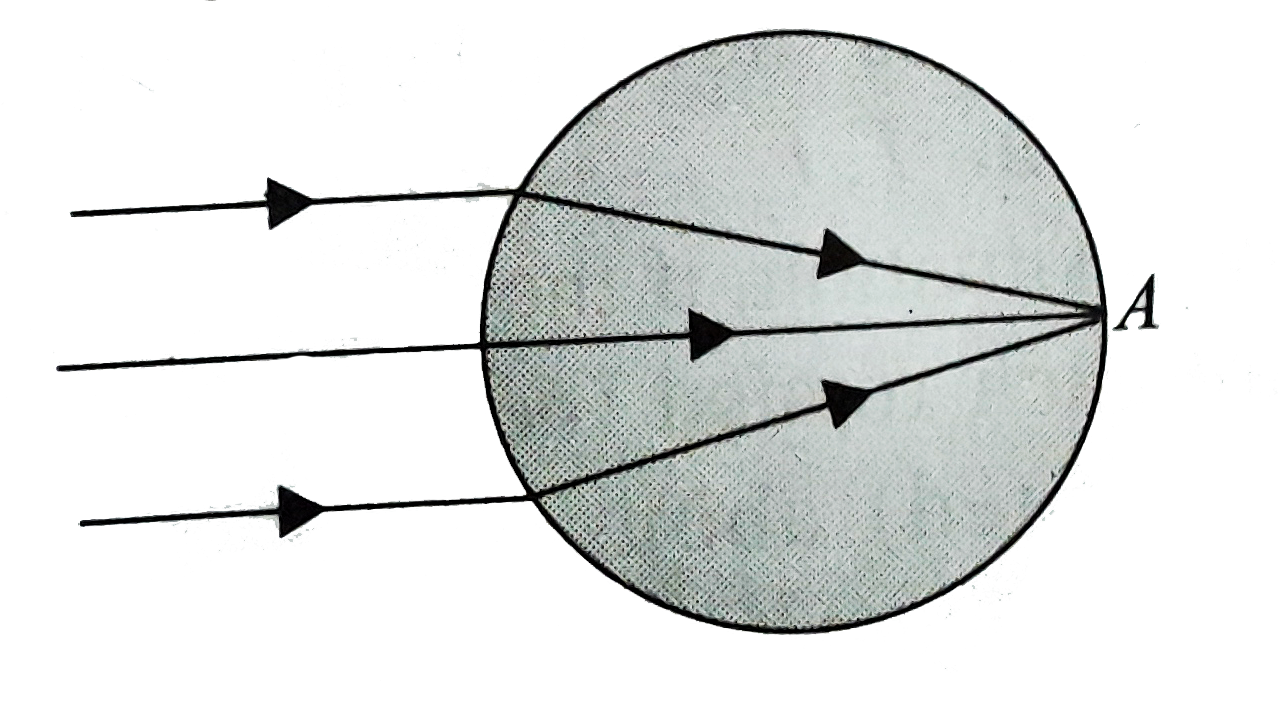
Q. If however thin beam is focussed at A, then find the refractive index of the sphere,
View SolutionA ray of light enters a spherical drop of water of refractive index p as shown in the figure.
An expression of the angle between incidence ray and emergent ray (angle of deviation) as shown in the figure is

View SolutionTwo light rays 1 and 2 are incident on two faces AB and AC on an isosceles prism as shown in the figure. The rays emerge from the side BC. Then,

View Solution
