A ray of light travelling in air is incident at 45∘ on a medium of refractive index √2. The angle of refractive in the medium is
A. 45∘
B.60∘
C.30∘
D.70∘
The correct Answer is:C
To solve the problem of finding the angle of refraction when a ray of light travels from air into a medium with a refractive index of √2, we can use Snell's Law. Here’s a step-by-step solution:
Step 1: Understand the Problem
We have a ray of light incident at an angle of 45∘ from air (where the refractive index n1=1) into a medium with a refractive index n2=√2. We need to find the angle of refraction r in the medium.
Step 2: Apply Snell's Law
Snell's Law states that:
n1sin(i)=n2sin(r)
Where:
- n1 = refractive index of the first medium (air) = 1
- i = angle of incidence = 45∘
- n2 = refractive index of the second medium = √2
- r = angle of refraction
Step 3: Substitute the Known Values
Substituting the known values into Snell's Law:
1⋅sin(45∘)=√2⋅sin(r)
Step 4: Calculate sin(45∘)
We know that:
sin(45∘)=1√2
So we can rewrite the equation as:
1⋅1√2=√2⋅sin(r)
Step 5: Rearrange the Equation
Rearranging gives:
sin(r)=1/√2√2=12
Step 6: Find the Angle r
Now we need to find the angle r such that:
sin(r)=12
The angle r that satisfies this equation is:
r=30∘
Conclusion
The angle of refraction in the medium is 30∘.
---
We have a ray of light incident at an angle of 45∘ from air (where the refractive index n1=1) into a medium with a refractive index n2=√2. We need to find the angle of refraction r in the medium.
Snell's Law states that:
n1sin(i)=n2sin(r)
Where:
- n1 = refractive index of the first medium (air) = 1
- i = angle of incidence = 45∘
- n2 = refractive index of the second medium = √2
- r = angle of refraction
Substituting the known values into Snell's Law:
1⋅sin(45∘)=√2⋅sin(r)
We know that:
sin(45∘)=1√2
So we can rewrite the equation as:
1⋅1√2=√2⋅sin(r)
Rearranging gives:
sin(r)=1/√2√2=12
Now we need to find the angle r such that:
sin(r)=12
The angle r that satisfies this equation is:
r=30∘
The angle of refraction in the medium is 30∘.
Topper's Solved these Questions
Similar Questions
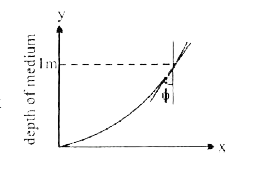
A ray of light travelling in air is incident at grazing angle (incidence angle =90∘) on a medium whose refractive index depends on the depth of the medium. The trajectory of the light in the medium is a parabola, y=2x2. Find, at a depth of 1 m in the medium
(i) the refractive index of the medium and
(ii) angle of incidence ϕ.
View SolutionDetermine the value of the angle of incidence for a ray of light travelling from a medium of refractive index μ1=√2 into the medium of refractive index μ2=1, so that it just grazes along the surface of separation.
View Solution
Knowledge Check
A ray of light is incident on a medium of refractive index √2 at an angle of incidence of 45∘. The ratio of the width of the incident beam in air to that of the refracted beam in the medium is
A(3/2)1/2B(2/3)1/2C3/2D2/3AN unpolarised beam of light is incident at the polarising angle on the surface of a transparent medium of refractive index 1.6. The angle of refraction in the medium is
A58∘B29∘C32∘D42∘A ray of light travels from a medium of refractive index n1 to
a medium of refractive index n2. If angle of incidence is i and
angle of refraction is r, than sinisinr is equal toAa n1Bb n2Cc n2n1Dd n1n2
Determine the value of the angle of incident for a ray of light travelling from a medium of refractive index μ1=√2 into the medium of refractive index μ2=1, so that it just grazed along the surface of separation.
View SolutionA ray of light travelling in air is incident on the plane surface of a transparent medium. The angle of incidence is 45∘ and the angle of refraction is 30∘ . Find the refractive index of the medium .
View SolutionA ray of light goes from a medium of refractive index n1 to a medium of refractive index n2. The angle of incidence is I and the angle of refraction is r. Then, sin i/sin r is equal to
View SolutionA ray of light in air is incident at an angle of 45∘ on the surface of separation of a medium. It is refracted in the medium at an angle of 30∘. What is the velocity of light in that medium ?
View SolutionA ray of light travelling in a transparent medium f refractive index μ, falls on a surface separating the medium from air at an angle of incidence of 45∘. For which of the following value of μ the ray can undergo total internal reflection ?
View Solution
