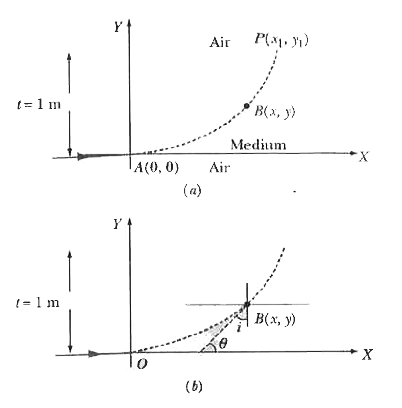
A ray of light travelling in air is incident at grazing angle (incident angle=90∘) on a long rectangular slab of a transparent medium of thickness t=1.0 (see figure). The point of incidence is the origin A(O,O) .The medium has a variable index of refraction n(y) given by :n(y)=[ky3/2+1]1/2 ,where k=1.0m−3/2.the refractive index of air is 1.0<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/NG_PHY_RO_C01_E01_029_Q01.pngwh=80%mx-autosty≤=background:white;><br>(i)Obta∈arelationbetweentheslopeofthetrajec→ryoftherayatap∮B(x,y)∈themediumandthe∈cnt∠attˆp∮<br>(ii)obta∈anequationforthetrajec→ryy(x)oftheray∈themedium.<br>(ii)Determinethec∞rd∈ates(x_(1),y_(1))ofthep∮P.where the ray the ray intersects upper surface of the slab -air boundary.
Indicate the path of the ray subsequently.
(1) In situation where refractive index changes only in one direction, medium can be considered as a collection of large number of the thin layers. Let refractive index be a function of y, that is n=f(y) then medium can be considered as to made up of a large number of thin slabs placed parallel to x axis and normal at any surface is parallel to x axis and normal at any surface is parallel to y axis.
(2) Although the refractive index is not constant, we cannot apply Snell.s laws here, but still we can divide the whole medium into thin layers as shown in Fig. 34-22. Within a layer, refractive index is constant. So here we have a case of many parallel slabs. We can apply Snell.s law here.
n1sinθ1=n2sinθ2=n3sinθ3=.....
nsinθ=constant
Calculations
(a) From Fig. 34-22b,
i+θ=90∘
Slope of the tangent =tanθ
=tan(90−i)=coti
(b) We know that at any point in the medium with variable refractive index n sin i constant, where n= refractive index at any point y and i=angle of incidence at any point y. Therefore,
nsini=1sin90∘
sini=1coseci=1√1+cot2i
Substituting the values (ky3/2+1)1/2, we get
1√1+m2=1
ky3/2+1=1+m2
Slope m=dydx=√ky3/4
y−3/4dy=√kdx.
On integrating both sides, we get
∫y0y−3/4dy=∫x0√kdx
4y1/4=x (since k=1)
y=x4256
(c ) For y=1m, x=4m
(d) Let αe be the angle of emergence in the air, then by Snell.s law ,
nesinαe=n1sinα1=1 (refractive index of air ne=1)
This gives
sinαe=1⇒αe=90∘
Thus, it emerges parallel to the incident ray , this could have been interpreted by Snell.s law too.
Topper's Solved these Questions
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Check point
6 Videos
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Problems
44 Videos
- GEOMETRICAL OPTICS : REFLECTION BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFLECTION EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
4 Videos
Similar Questions
A ray of light travelling in air is incident at grazing angle (incident angle = 90∘) on a large rectangular slab of a transparent medium of thickness t = 1 m. The point of incidence js the origin A (0, 0). The medium has a refractive index of n (y) given
n(y)=(9ky32+1)12
Where K = (meter)−32, The refractive index of air is 1.
Obtain the equation for the trajectory y(x) of the ray of the medium.
View SolutionA ray of light travelling in air is incident on the plane surface of a transparent medium. The angle of incidence is 45∘ and the angle of refraction is 30∘ . Find the refractive index of the medium .
View Solution
Knowledge Check
A ray of light travelling in air is incident at 45∘ on a medium of refractive index √2. The angle of refractive in the medium is
AA. 45∘BB.60∘CC.30∘DD.70∘A ray of light is incident at an angle of incidence 45∘ on an equilateral prism and emerge at an angle 45∘ then the refractive index of the medium of the prism is:
A2B√2C1√2D√3A ray of light travelling in air is incident at grazing incidence on a slab with variable refractive index, n (y)=[ky3/2+1]1/2 where k=1m−3/2 and follows path as shown in the figure. What is the total deviation produced by slab when the ray comes out.
 A60∘B53∘Csin−1(4/9)Dno deviation at all
A60∘B53∘Csin−1(4/9)Dno deviation at all
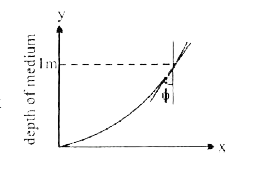
A ray of light travelling in air is incident at grazing angle (incidence angle =90∘) on a medium whose refractive index depends on the depth of the medium. The trajectory of the light in the medium is a parabola, y=2x2. Find, at a depth of 1 m in the medium
(i) the refractive index of the medium and
(ii) angle of incidence ϕ.
View SolutionA ray of light is incident on a glass slab at grazing incidence. The refractive index of the material of the slab is given by μ=√(1+y) . If the thickness of the slab is d=2m, determing the equation of the trajectory of the ray inside the slab and the coordinates of the point where the ray exits from the slab. Take the origin to be at the point of entry of the ray.
View SolutionA ray of light is incident at an angle of 60∘ on one face of a rectangular glass slab of thickness 0.1m, and refractive index 1.5.Calculate the lateral shift produced.
View SolutionThe refractive index of a medium is √3. What is the angle of refraction, if the unpolarised light is incident on it at the polarising angle of the medium ?
View SolutionA ray of light is incident on a glass slab at grazing incidence. The refractive index of the material of the slab is given by μ=√1+√y. If the thickness of the slab is d, determine the equation ofthe trajectory of the ray inside the slab and the coordinates of the point where the ray exits from the slab. Take the origin to be at the point of entry of the ray.
View Solution
